谁是你的优先级呢？

---

目录

1、优先级队列

1.1 优先级队列概念

1.2 堆的概念

1.3 堆的存储结构

2、模拟实现优先级队列

2.1 成员变量的设定

2.2 根据数组构造出一个堆

2.3 向下调整

2.4 createHeap 方法实现 

2.5 offer 方法实现

2.6 poll 方法实现

3、PriorityQueue 的使用

3.1 注意事项

3.2 PriorityQueue 如何创建大堆？

3.3 PriorityQueue 的扩容机制

4、top-k 问题

---

1、优先级队列

1.1 优先级队列概念

既然是优先级队列，我们注意优先级这个词，前面讲队列的时候，是先进先出，而优先级队列可不一定是这样，举个生活中的例子， 你刚打开手机游戏，但是这时候你女朋友敲门回来了，你是不是得先去给女朋友开门？虽然是游戏先打开的，但是得先开门去，这就有一个优先级的问题。我们数据也是一样的，重要的数据先解决，不重要的数据是不是就可以放一放？

为了解决上述的情况，Java集合中就提供了一种始终返回最高优先级的对象的集合:PriorityQueue

在JDK1.8中，PriorityQueue 底层使用了堆，而在模拟实现优先级队列前我们需要了解堆的特性。

1.2 堆的概念

回顾下我们之前完全二叉树的概念，每一层的节点都是从左往右的，依次排列，中间不能空着元素。简单来说就是这样一个概念，那么完全二叉树跟我们今天要讲的堆又有什么关系呢？

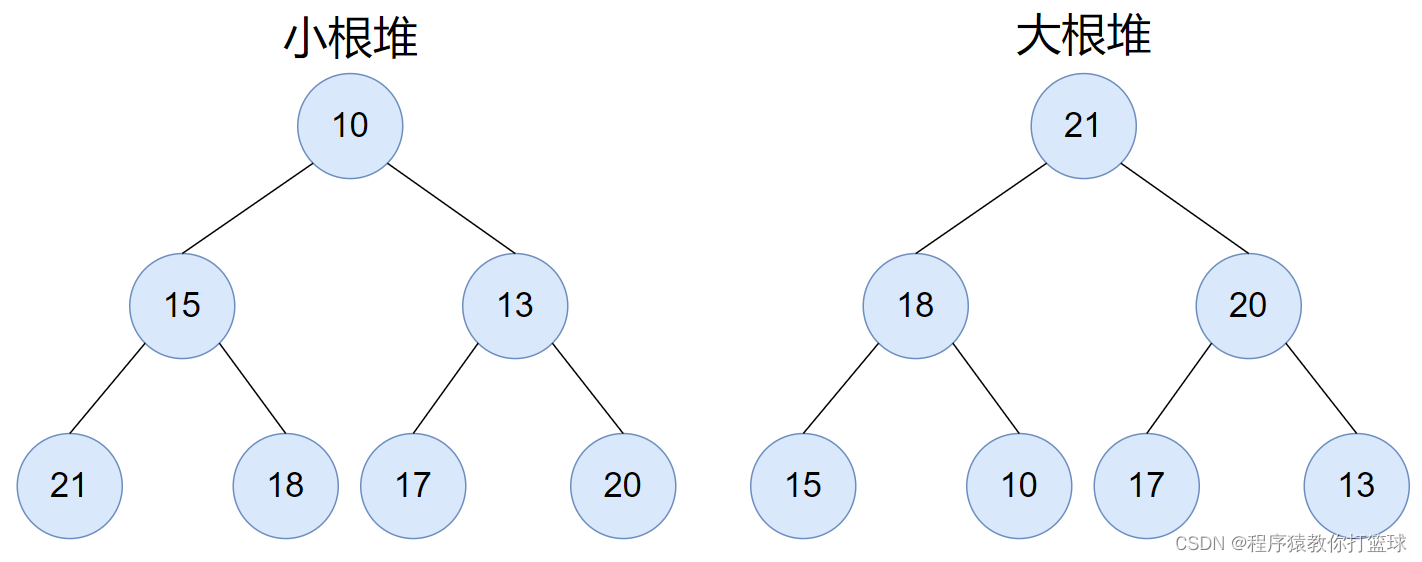
堆是一个(特殊的)完全二叉树，每个父节点都不大于或者不小于自己的孩子节点，层序遍历这个二叉树，顺序的放入一个数组中，这就是堆的存储。从逻辑上来说，堆是一棵完全二叉树，从存储底层来说，堆底层是一个数组。

大根堆：每个根节点都大于子节点

小根堆：每个根节点都小于子节点

1.3 堆的存储结构

前面说过，堆的底层其实是一个数组，这里有个问题，为什么堆必须是一棵完全二叉树呢？通过下面的图我们来简单了解下：

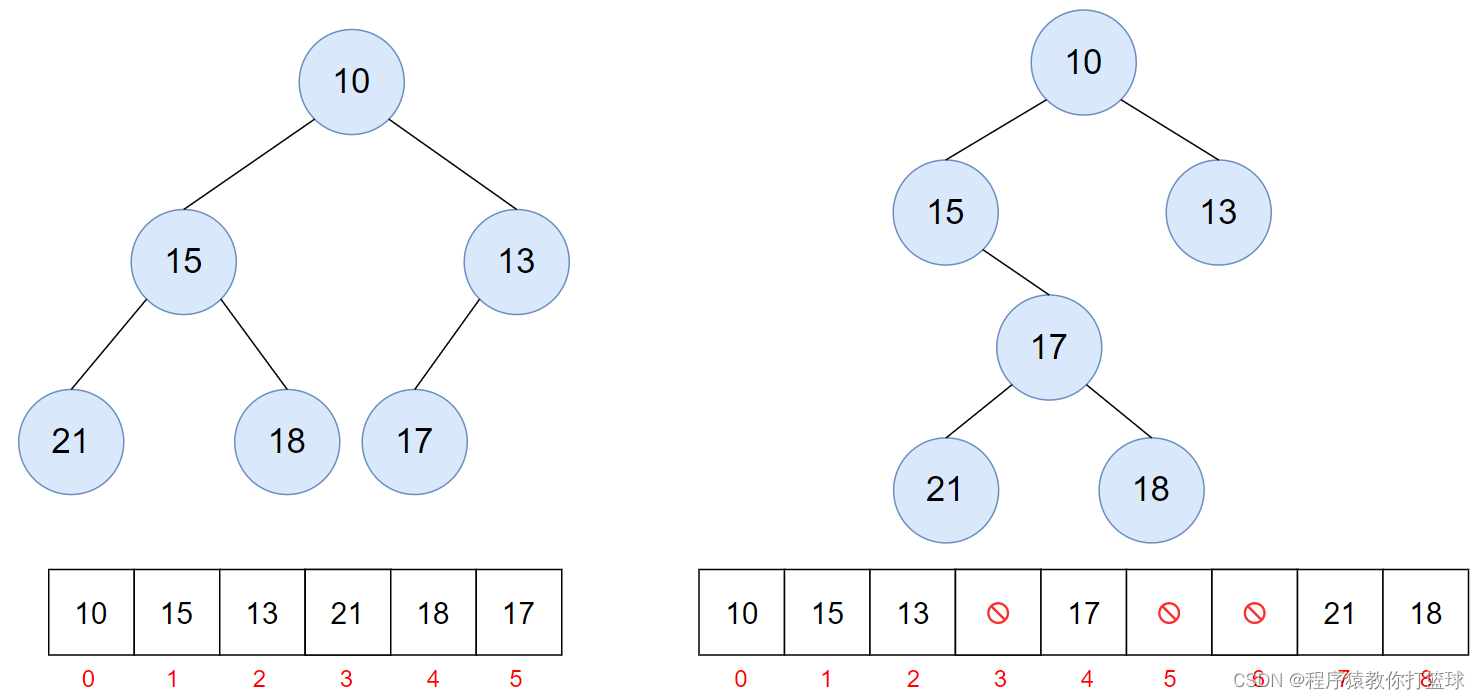
堆其实是按照二叉树的层序遍历来放入元素的，由上图也可知，对于非完全二叉树势必会造成空间的浪费，因为为了能够还原成二叉树，所以空间中必须要存储节点，所以本质上堆是一棵完全二叉树的原因是可以有效的利用空间，减少空间的浪费！

有了上述的知识，这里我们来看几个性质( i 为数组中的下标)：

• 如果 i 为 0，则表示该节点为根节点，否则 i 节点的父节点为 （i - 1）/ 2 
• 如果 2 * i + 1 小于有效元素个数，那么左子节点的下标为 2 * i + 1，否则没有左子孩子
• 如果 2 * i + 2 小于有效元素个数，那么右子节点的下标为 2 * i + 2，否则没有右子孩子 

---

2、模拟实现优先级队列

2.1 成员变量的设定

public class MyPriorityQueue {
    private int[] elem; //存放数据的数组
    private int size; //堆中有效数据个数
    private static final int DEFAULT_CAPACITY = 10; //默认容量
    private boolean isFirstInsert; //判断是否第一次插入数据
}

对于最后这个 isFirstInsert 可能有点不明白为啥这样设计，到后面我用到的时候会介绍。

2.2 根据数组构造出一个堆

这里我们可以把实现写在构造方法中，因为当传过来数组的时候，我们要利用传过来的数组来初始化我们的成员变量。

public MyPriorityQueue() {
    this.elem = null;
    this.isFirstInsert = true;
    this.size = 0;
}
public MyPriorityQueue(int[] array) {
    this.isFirstInsert = false; //改为false表示不是第一次往堆中插入元素了
    int len = array.length;
    this.elem = Arrays.copyOf(array,len);
    this.size = len;
    createHeap(); //将数组构造成堆
}

我们主要看第二个构造方法，这里 isFirstInser 为啥设置成 false，放到 offer 方法实现中讲解，这里可以看到用了很简单的方式来初始化成员变量，最主要的是 createHeap 方法，当我们去实现这个方法之前，需要简单了解下什么是向下调整。

2.3 向下调整

什么是向下调整算法呢？简单来说就是从根节点往下调整，调整为大根堆或者小根堆，但前提是根节点的左子树和右子树都必须是小堆或大堆才能进行向下调整。（后序我们都采用小堆来举例）

这里我们来简单举两个例子大家来看一看，为什么左子树和右子树必须是小堆才能进行向下调整呢？

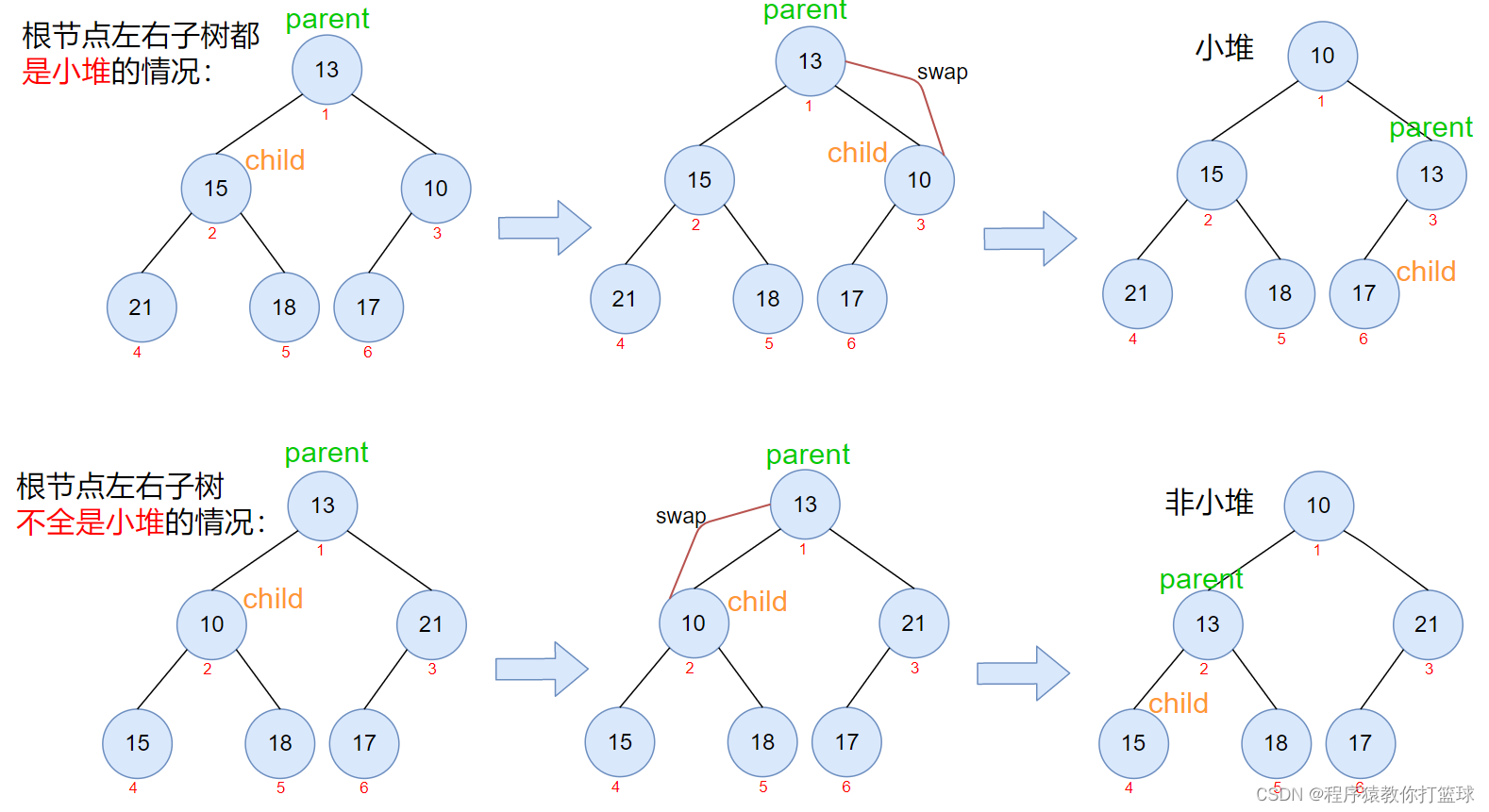
向下调整解释(小堆)：从根节点开始，选出左右孩子的较小值，去跟根节点比较，也就是parent和child，如果 parent 比 child 大，那么就需要交换，接着调整 parent 的位置，直到左右孩子都大于 parent 停止，这样就形成了一个小根堆。

通过图片也能看出，进行向下调整的前提就是根节点的左右子树必须都为小堆(或大堆)，所以向下调整算法代码可以是这个样子的：

private void shiftDown(int parent) {
    int len = size();
    int child = parent * 2 + 1;
    // 保证parent有左孩子的情况
    while (child < len) {
        // child+1<len 保证该parent有右孩子的情况
        // 找出较小的孩子节点
        if (child + 1 < len && this.elem[child] > this.elem[child + 1]) {
            child++; //走到这表示左孩子大于右孩子,调整child位置
        }
        // 走到这判断parent节点是否大于两个孩子的较小值,如果大于则交换他们两个的值
        if (this.elem[parent] > this.elem[child]) {
            swap(parent, child);
            parent = child; //更新parent的位置,接着往下调整
            child = parent * 2 + 1; //更新child位置
        } else {
            // 走到这,表示从parent往下的节点都比parent小,满足小根堆,不需要向下调整了
            break;
        }
    }
}
private void swap(int parent, int child) {
    int tmp = this.elem[parent];
    this.elem[parent] = this.elem[child];
    this.elem[child] = tmp;
}

时间复杂度：在最坏的情况下，从根一路比到叶子节点，比较的次数为完全二叉树的高度，即时间复杂度为 O(logn)

但是问题来了，如果我的左右子树不是小堆 (或大堆) 那不就用不了向下调整的算法了吗？谁知道我当前对象存储的数组一定是满足向下调整的的条件的吗？ 

2.4 createHeap 方法实现 

顺着上述的问题，如果不满足向下调整的条件咋办？那该如何用传过来的数组建堆呢？ 

首先把数组看作成一棵完全二叉树，由二叉树的性质可以知道，一棵二叉树由左子树和右子树构成，从左子树的根开始也可也看作一棵二叉树，右子树的根同理，那么是不是可以从最后一棵子树开始调整，如果从后往前每棵子树都是小堆，那个时候直接调整根节点即可！

到这里，问题变成了如何找到最后一棵子树的根节点？

利用二叉树的性质，找到数组最后一个元素，就可以求出父节点，也就是 (child - 1) / 2 就能得到 parent 的位置。最后一棵子树调完了，调倒数第二棵，即 parent--，直到 parent 小于 0 ，至此堆构建完成！

于是我们 createHeap 方法就可以这样来实现：

private void createHeap() {
    for (int parent = (size() - 1) / 2; parent >= 0; parent--) {
        shiftDown(parent); //从最后一个非叶子的根节点开始调整,一直调整到根节点
    }
}

 我们就拿上述图中的例子来测试一下：

public class TestMyPriorityQueue {
    public static void main(String[] args) {
        int[] array = { 13, 10, 21, 15, 18, 17 };
        System.out.println("建堆前:" + Arrays.toString(array));
        MyPriorityQueue priorityQueue = new MyPriorityQueue(array);
        System.out.println("建堆后:" + priorityQueue);
    }
}

通过测试样例我们发现，堆已经构建成功了，这就是 createHeap 方法的实现，在回过头去看我们的构造方法，是不是就能看懂了呢？

public MyPriorityQueue(int[] array) {
    this.isFirstInsert = false; //改为false表示不是第一次往堆中插入元素了
    int len = array.length;
    this.elem = Arrays.copyOf(array, len);
    this.size = len;
    createHeap(); //将数组构造成堆
}

2.5 offer 方法实现

当我们想往优先级队列中插入一个元素的时候，肯定是往 size 位置放，但是插入之后，是不是也得保证是小堆 (或大堆) ？如果是第一次插入元素呢？就不用调整了，否则需要从最后一个元素往上调整，保证插入元素之后还是小堆(或大堆)，我们叫做向上调整。

我们先来简单看一下代码：

public void offer(int val) {
    if (isFirstOffer(val)) {
        return;
    }
    if (isFull()) {
        grow(); //扩容
    }
    this.elem[size] = val;
    // 插入之后进行向上调整
    shiftUp(this.size++);
}
private boolean isFirstOffer(int val) {
    // 第一次插入的情况
    if (isFirstInsert) {
        this.elem = new int[DEFAULT_CAPACITY];
        this.elem[size++] = val;
        isFirstInsert = false; // 改为false下次就不是第一次插入的了
        return true;
    }
    return false;
}
private boolean isFull() {
    return size() == this.elem.length;
}
private void grow() {
    // 当前数组长度两倍扩容
    this.elem = Arrays.copyOf(this.elem, this.elem.length * 2);
}

如果是第一次插入元素，我们需要先给 elem 数组开辟空间，默认大小是 10，最重要的是向上调整的方法，这里我们需要单独来分析下：

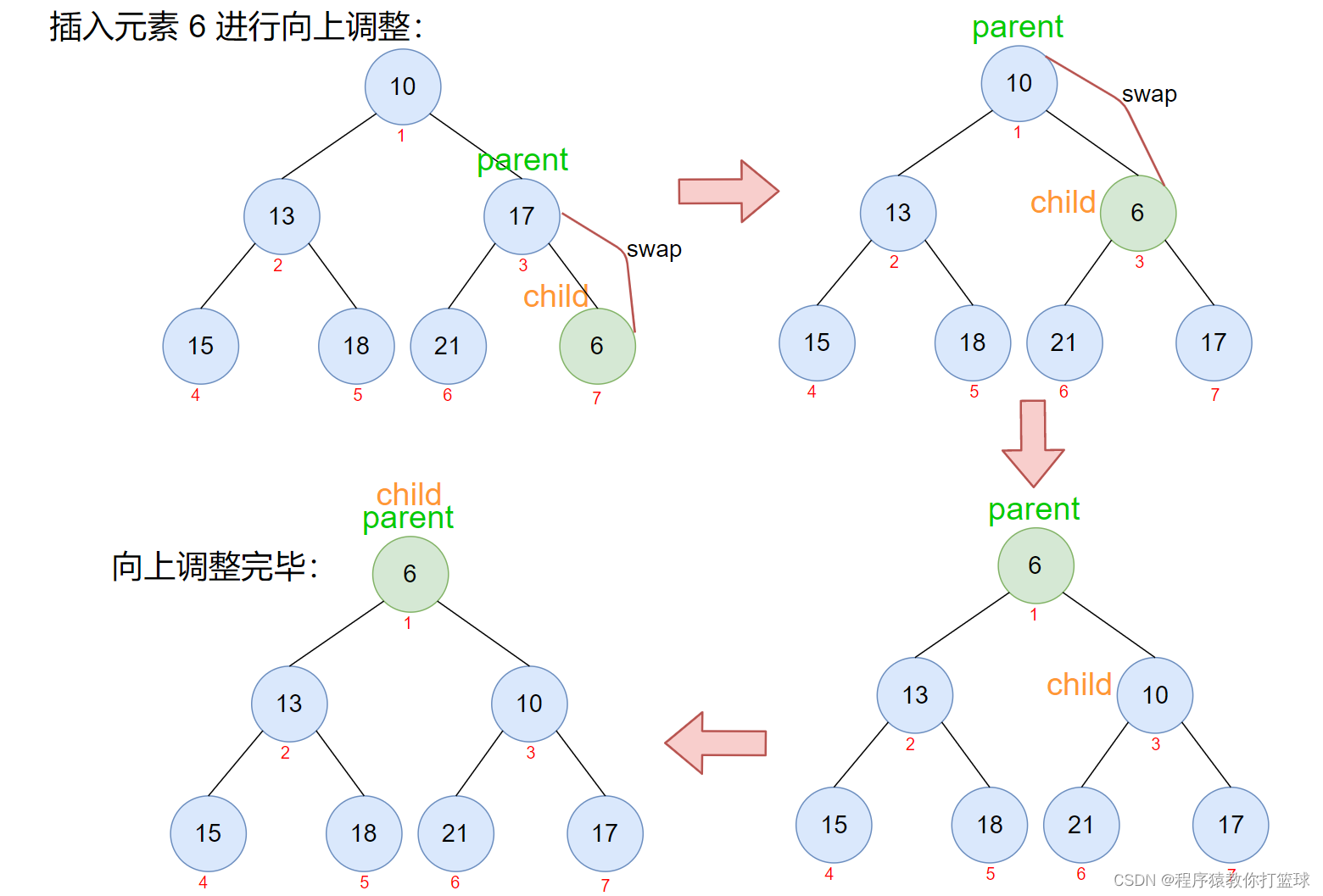
向上调整解释(小堆)：从最后一个插入节点的位置开始，定义当前位置为 child，如果当前节点的父节点即 parent，如果 parent 大于 child 则进行交换，接着更新 child 的位置，和 parent 的位置，直到 child 为根节点的位置，则向上调整完毕，如果中途发现 parent 不大于 child 则可以直接退出，因为已经满足小堆的条件了。

这里有些童鞋会担心一个问题，交换之后怎么保证这个子树也是小堆呢？别忘了，在进行插入之前已经是小堆了，所以不存在交换之后不满足堆的性质！

private void shiftUp(int child) {
    //找到父节点
    int parent = (child - 1) / 2; //找到父节点
    // 如果child等于0了,表示根节点已经调整完成了
    while (child > 0) {
        if (this.elem[parent] > this.elem[child]) {
            swap(parent, child);
            child = parent; //更新孩子的位置
            parent = (child - 1) / 2; //更新父节点的位置
        } else {
            return; //如果根节点不大于孩子节点,表明已经满足小堆的性质了
        }
    }
}

建堆的时间复杂度约等于 O(n)，感兴趣的小伙伴可以下去自行推导下。 

2.6 poll 方法实现

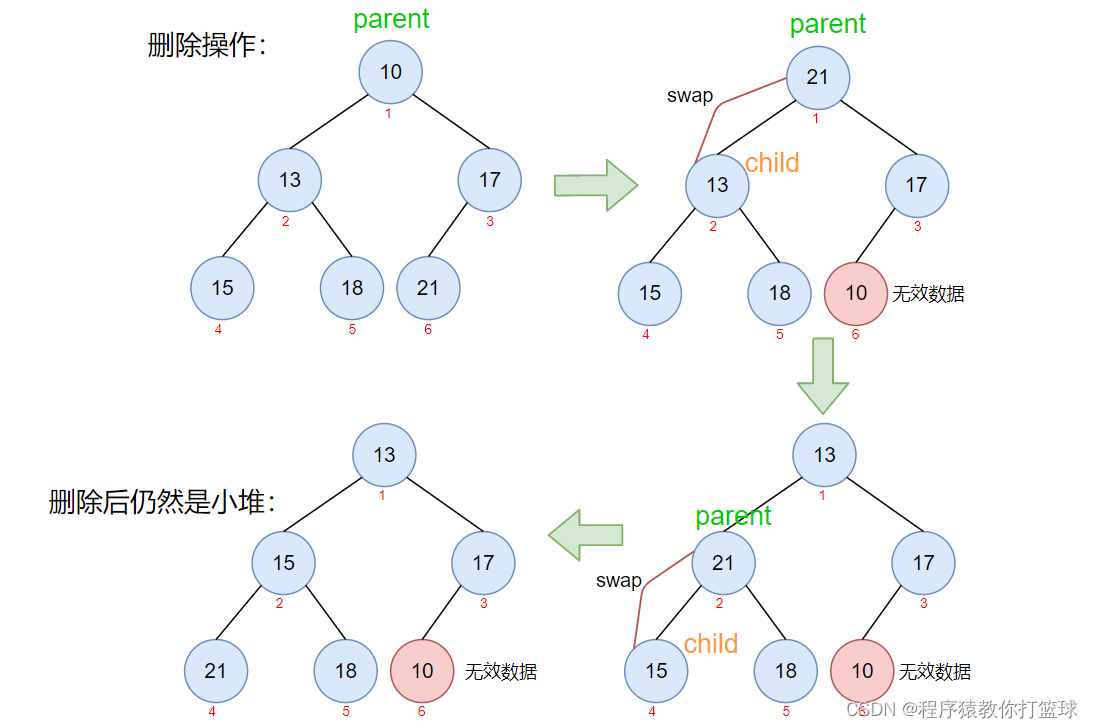
出堆肯定每次是出堆顶的元素，这样才能体现出堆的优先级，如何出堆顶呢？把数组的所有元素往前覆盖吗？那这样的话还要从最后一棵子树开始调整太慢了。

在C语言阶段，博主讲解过，计算机中的删除，本质上是将数据设置成无效，新增的数据可以直接覆盖无效的数据，那么我们可以将当前堆顶元素记录下来，然后堆尾最后一个元素覆盖掉堆顶的元素，即当前的根节点改为最后一个节点，所以我们只需要从根节点进行一遍向下调整即可。

public int poll() {
    if (isEmpty()) {
        throw new DataException("堆中没有元素！！！");
    }
    int oldTop = this.elem[0];
    this.elem[0] = this.elem[--size];
    shiftDown(0);
    return oldTop;
}

---

3、PriorityQueue 的使用

3.1 注意事项

• PriorityQueue中放置的元素必须要能够比较大小，不能插入无法比较大小的对象，否则会抛出 ClassCastException异常
• 不能插入null对象，否则会抛出NullPointerException
• 没有容量限制，可以插入任意多个元素，其内部可以自动扩容
• 插入和删除元素的时间复杂度为 O(logn)
• PriorityQueue默认情况下是小堆 —— 即每次获取到的元素都是最小的元素

上面有一条说到，存放的元素必须是可比较的，而且默认是小堆，那么如果我想是大堆该怎么办呢？

3.2 PriorityQueue 如何创建大堆？

方法1：传一个比较器过去即可，自定义一个比较器，实现 Comparator 接口，重写 compare 方法即可。

至于 PriorityQueue 里面的一些构造方法，博主还是希望各位小伙伴能下去自己看看，多动手，光看我文章是没用的。

这里我们来演示下建一个大堆：

static class IntCmp implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {
        return o2 - o1;
    }
}
public static void main(String[] args) {
    PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new IntCmp());
    priorityQueue.offer(3);
    priorityQueue.offer(10);
    priorityQueue.offer(8);
    System.out.println(priorityQueue.peek());
}

方法2：传一个匿名内部类对象过去，里面重写了 Comparator 方法即可。

public static void main(String[] args) {
    PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o2 - o1;
        }
    });
    priorityQueue.offer(3);
    priorityQueue.offer(10);
    priorityQueue.offer(8);
    System.out.println(priorityQueue.peek());
}

由于是大堆，他们最终的结果都是一样的：

10

3.3 PriorityQueue 的扩容机制

这里我们直接来看这里面的源码（JDK1.8）：

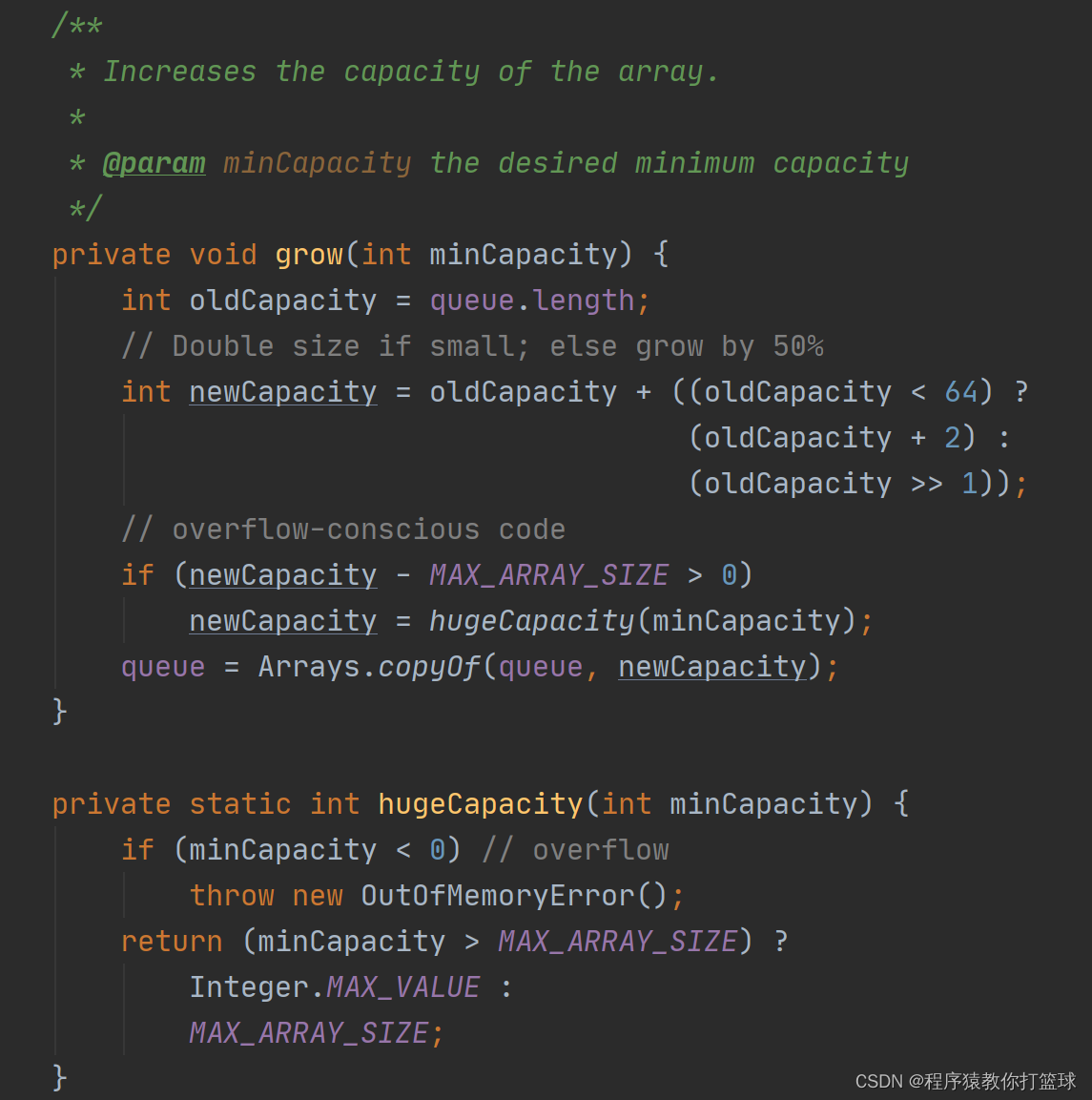
通过第二行代码，当容量小于 64 时，新的容量是原来的2倍+2，当容量大于 64 时，新的容量是原来的1.5倍。

往后走，如果最后新的容量大于最大的数组值，也就是 MAX_ARRAY_SIZE 时，就按照 MAX_ARRAY_SIZE 来进行扩容。

---

4、top-k 问题

面试题 17.14.最小K个数【题目来源：Leetcode】

设计一个算法，找出数组中最小的k个数。以任意顺序返回这k个数均可。

示例：

输入： arr = [1,3,5,7,2,4,6,8], k = 4
输出： [1,2,3,4]

这道题的解法其实蛮多的，比如先将数组排升序，然后取前 k 个元素就可以了，假如十个人九个人在面试的时候写出这样的代码，就吸引不到面试官的眼球了。

既然本期介绍的是优先级队列(堆)，那我们就用 PriorityQueue 来解决这个问题。

可能直接一想，蛮简单啊，建小堆，堆的大小为数组长度就可以了，遍历数组一遍放入堆中，直接取堆顶前 k 个元素放入返回数组中就ok了。

这样做确实没问题，假如这个时候面试官问你，假如从十万个数据中取前五个最小的数据呢？那你要开辟的数组长度岂不是得是十万啊？太浪费空间了吧，那假如是一百万个数据中取前五个呢？

所以上述思路不行，特殊情况下空间浪费太大了，这里博主就来介绍一种方法，建大堆，堆的长度为 k，当我们 offer 前 k 个元素进去之后，就每次拿堆顶的元素和剩下的数组元素比较，如果堆顶元素大于我后面的元素，我就出堆顶元素，接着入堆，这样一来最终堆里面放着的就是前 k 个最小的了！

public static int[] smallestK(int[] arr, int k) {
    if(arr == null || k == 0) {
        return new int[0];
    }
    // 建大堆,如果堆顶元素大于我后面要放入的元素,则出队列,剩下的五个就是最小的五个
    PriorityQueue<Integer> pQueue = new PriorityQueue<>(k, new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o2 - o1;
        }
    });
    for (int i = 0; i < arr.length; i++) {
        if (i < k) {
            pQueue.offer(arr[i]); //先入k个元素
        } else {
            int val = pQueue.peek();
            // 遍历后序的元素,发现堆顶元素大于后序元素就出堆
            if (val > arr[i]) {
                pQueue.poll();
                pQueue.offer(arr[i]);
            }
        }
    }
    int[] ret = new int[k];
    int i = 0;
    while (!pQueue.isEmpty()) {
        ret[i++] = pQueue.poll();
    }
    return ret;
}

最后，关于优先级队列的一些方法，大家可以自行下去查查文档，或者看看源码，多多练习练习。

---

下期预告：【Java数据结构】排序算法 (上)