一,半群算法
//半群
class SemiGroup
{
public:
//枚举只去掉1个数(v.size()>1),剩下的数做p累积运算的结果
template<typename T, typename Tfunc>
static vector<T> allExceptOne(vector<T>& v, Tfunc p) {
vector<T>left(v.size() - 1), right(v.size() - 1);
T x = v[0];
for (int i = 1; i < v.size(); i++)left[i - 1] = x, x = p(x, v[i]);
x = v.back();
for (int i = int(v.size()) - 2; i >= 0; i--)right[i] = x, x = p(v[i], x);
vector<T>ans(1, right[0]);
for (int i = 0; i < left.size() - 1; i++)ans.push_back(p(left[i], right[i + 1]));
ans.push_back(left.back());
return ans;
}
};力扣 2003. 每棵子树内缺失的最小基因值
有一棵根节点为 0 的 家族树 ,总共包含 n 个节点,节点编号为 0 到 n - 1 。给你一个下标从 0 开始的整数数组 parents ,其中 parents[i] 是节点 i 的父节点。由于节点 0 是 根 ,所以 parents[0] == -1 。
总共有 105 个基因值,每个基因值都用 闭区间 [1, 105] 中的一个整数表示。给你一个下标从 0 开始的整数数组 nums ,其中 nums[i] 是节点 i 的基因值,且基因值 互不相同 。
请你返回一个数组 ans ,长度为 n ,其中 ans[i] 是以节点 i 为根的子树内 缺失 的 最小 基因值。
节点 x 为根的 子树 包含节点 x 和它所有的 后代 节点。
示例 1:
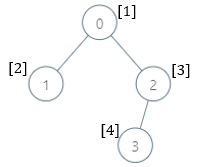
输入:parents = [-1,0,0,2], nums = [1,2,3,4] 输出:[5,1,1,1] 解释:每个子树答案计算结果如下: - 0:子树包含节点 [0,1,2,3] ,基因值分别为 [1,2,3,4] 。5 是缺失的最小基因值。 - 1:子树只包含节点 1 ,基因值为 2 。1 是缺失的最小基因值。 - 2:子树包含节点 [2,3] ,基因值分别为 [3,4] 。1 是缺失的最小基因值。 - 3:子树只包含节点 3 ,基因值为 4 。1是缺失的最小基因值。
示例 2:
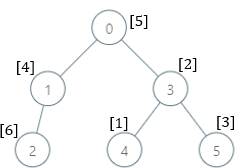
输入:parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3] 输出:[7,1,1,4,2,1] 解释:每个子树答案计算结果如下: - 0:子树内包含节点 [0,1,2,3,4,5] ,基因值分别为 [5,4,6,2,1,3] 。7 是缺失的最小基因值。 - 1:子树内包含节点 [1,2] ,基因值分别为 [4,6] 。 1 是缺失的最小基因值。 - 2:子树内只包含节点 2 ,基因值为 6 。1 是缺失的最小基因值。 - 3:子树内包含节点 [3,4,5] ,基因值分别为 [2,1,3] 。4 是缺失的最小基因值。 - 4:子树内只包含节点 4 ,基因值为 1 。2 是缺失的最小基因值。 - 5:子树内只包含节点 5 ,基因值为 3 。1 是缺失的最小基因值。
示例 3:
输入:parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8] 输出:[1,1,1,1,1,1,1] 解释:所有子树都缺失基因值 1 。
提示:
n == parents.length == nums.length2 <= n <= 105- 对于
i != 0,满足0 <= parents[i] <= n - 1 parents[0] == -1parents表示一棵合法的树。1 <= nums[i] <= 105nums[i]互不相同。
思路:
2次dfs
第一次dfs,把每颗子树的所有节点的最小值算出来。
第二次dfs,根据父节点的最小缺失值,算出所有子节点的最小缺失值。
具体来说,子节点的最小缺失值是3个值的最小值,这3个分别是父节点的最小缺失值、父节点的值、所有兄弟节点及其子节点的最小值。
class Solution {
public:
vector<int> smallestMissingValueSubtree(vector<int>& parents, vector<int>& nums) {
int n = parents.size();
sons.resize(n);
mins.resize(n);
ans.resize(n);
for (int i = 1; i < parents.size(); i++)sons[parents[i]].push_back(i);
getMin(nums, 0);
map<int, int>m;
for (auto x : nums)m[x]++;
int minMiss = 1;
while (m[minMiss])minMiss++;
dfs(nums, 0, minMiss);
return ans;
}
private:
int getMin(vector<int>& nums,int id) {
int ans = nums[id];
for (auto son : sons[id])ans = min(ans, getMin(nums, son));
return mins[id]=ans;
}
void dfs(vector<int>& nums,int id,int miss) {
ans[id] = miss;
miss = min(miss, nums[id]);
if (sons[id].size() <= 1) {
for (auto son : sons[id])dfs(nums, son, miss);
return;
}
vector<int>sonMin;
for (auto son : sons[id])sonMin.push_back(mins[son]);
auto otherMin = SemiGroup::allExceptOne(sonMin, [](int a, int b) {return min(a, b); });
for (int i = 0; i < sons[id].size(); i++) {
dfs(nums, sons[id][i], min(miss, otherMin[i]));
}
}
private:
vector<vector<int>>sons;
vector<int>mins;
vector<int>ans;
};力扣 2680. 最大或值
给你一个下标从 0 开始长度为 n 的整数数组 nums 和一个整数 k 。每一次操作中,你可以选择一个数并将它乘 2 。
你最多可以进行 k 次操作,请你返回 nums[0] | nums[1] | ... | nums[n - 1] 的最大值。
a | b 表示两个整数 a 和 b 的 按位或 运算。
示例 1:
输入:nums = [12,9], k = 1 输出:30 解释:如果我们对下标为 1 的元素进行操作,新的数组为 [12,18] 。此时得到最优答案为 12 和 18 的按位或运算的结果,也就是 30 。
示例 2:
输入:nums = [8,1,2], k = 2 输出:35 解释:如果我们对下标 0 处的元素进行操作,得到新数组 [32,1,2] 。此时得到最优答案为 32|1|2 = 35 。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 1091 <= k <= 15
思路:
k次操作一定会用完,而且一定会加在同一个数上,所以只需要枚举除了这个数之外,其他的数的或运算总结果。
或运算是环非域,但是这里只需要用到半群的结合性。
class Solution {
public:
long long maximumOr(vector<int>& nums, int k) {
if (nums.size() == 1)return nums[0] << k;
auto x = SemiGroup::allExceptOne(nums, [](int a, int b) {return a|b; });
long long ans = 0;
for (int i = 0; i < x.size(); i++)ans = max(ans, ((long long)nums[i] << k) | x[i]);
return ans;
}
};