整体思想就是根据预积分的公式，把已知量和未知量各放到一边，因为前面的数据都是变换到$c_0$下的，不是真正意义上和重力对齐的世界坐标，然后位移和速度的预积分中会用到加速度计获取的重力加速度g，但是这个重力g是没有和世界的重力方向对齐的，所以里面就存在了未知量，通过每组预积分的数据联立起来构成一个大矩阵对重力向量进行求解，这里是求解了重力方向（对于起始帧$c_0$的重力方向），重力大小也有，不过不准确，所以后续还会利用重力先验对方向进行调整

有个小问题：这个预积分前面不是也会涉及重力吗，是直接不理会当作影响不大来进行处理？那这个已知量里面也包含里一定的未知量的积分影响在里面，待我看下代码确定一下整体的初始化流程和思想，后续会出篇整体初始化思想流程

关于位移的预积分量的定义，把 $c_0$ 换成 $w$ 就是之前的式子了，因为重力还没对齐所以只转换到 $c_0$ 坐标系下，就是系统开始的第一帧下

先对平移进行推导

上一节零偏估计里面推导出这个式子

代入进去则有
$R_{c_0}^{b_k}(s{P}_{c_{k+1}}^{c_0}-R_{b_{k+1}}^{c_0}\cdot P_c^b)=R_{c_0}^{b_k}[s{P}_{c_k}^{c_0}-R_{b_k}^{c_0}\cdot P_c^b+R_{c_0}^{b_k}\cdot v^{b_k}\cdot \Delta t-\frac{1}{2}{g}^{c_0}\Delta t^2+\alpha ]$
原本的 $v_{b_k}^{c_0}$ 指的是再 $c_0$ 坐标系下 $b_k$ 的速度，现在直接拿在 $b_k$ 系下的速度通过旋转矩阵进行变换，其实意思是一样的。
现在把已知量放左边，未知量放右边
$\alpha -P_c^b\cdot R_{c_0}^{b_k}\cdot R_{b_{k+1}}^{c_0}\cdot P_c^b=R_{c_0}^{b_k}(P_{c_{k+1}}^{c_0}-P_{c_k}^{c_0})s-v^{b_k}\Delta t+\frac{1}{2}{R}_{c_0}^{b_k}{g}^{c_0}\Delta t^2$
左边都是已知量，最后是一个 $3\times 1$ 的一个向量
上面的式子就和论文中的公式对应了

对速度进行推导

根据原始预积分的定义有
$R_{c_0}^{b_k}\cdot V_{b_{k+1}}^{c_0}=R_{c_0}^{b_k}(V_{b_k}^{c_0}-g^{c_0}\cdot \Delta t)+\beta$
然后变换一下表达方式，含义是不变的
$=>R_{c_0}^{b_k}\cdot R_{b_{k+1}}^{c_0}\cdot V^{b_{k+1}}=R_{c_0}^{b_k}(R_{b_k}^{c_0}\cdot V^{b_k}-g^{c_0}\cdot \Delta t)+\beta$
同样把已知量放左边，未知量放右边
$=>\beta =-V^{b_k}+R_{c_0}^{b_k}\cdot R_{b_{k+1}}^{c_0}\cdot V^{b_{k+1}}+R_{c_0}^{b_k}\cdot g^{c_0}\cdot \Delta t$

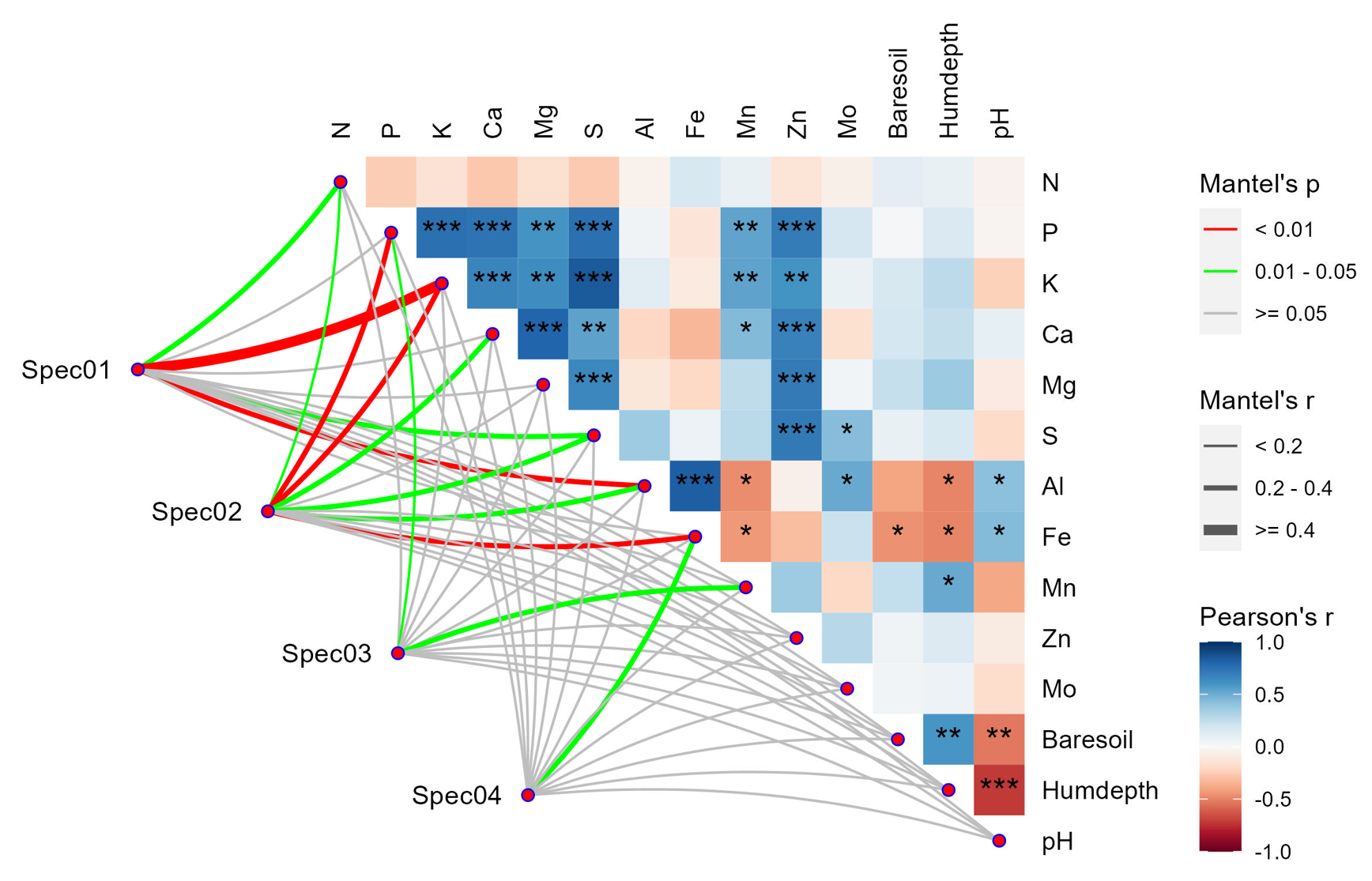
第 k 到 k+1 都会产生上面两个式子，会有很多个这种式子拼起来

构成 $Hx=b$ 的矩阵方程，代码中就是一些矩阵拼接的操作
$x=[v_k,v_{k+1},g,s]\in 10\times 1$，所以 $H属于10\times 10$ ，$b\in 10\times 1$，实际上由于有多组数据，10 会变成 N，速度，重力都是3维的，尺度因子是1，所以每一组就是 10

有多个数据则矩阵写为，通过对每一组数据进行矩阵分块填入这个大矩阵里面，然后一次性求解出所有速度、重力和尺度

求解后获得重力向量
然后根据当地的重力先验来对刚才算出来的重力进行修正