LeetCode：2003. 每棵子树内缺失的最小基因值（C++）

news2024/10/6 18:27:23

2003. 每棵子树内缺失的最小基因值

题目描述：

实现代码与解析：

dfs + 启发式合并

原理思路：

2003. 每棵子树内缺失的最小基因值

题目描述：

有一棵根节点为 0 的 家族树 ，总共包含 n 个节点，节点编号为 0 到 n - 1 。给你一个下标从 0 开始的整数数组 parents ，其中 parents[i] 是节点 i 的父节点。由于节点 0 是根，所以 parents[0] == -1 。

总共有 105 个基因值，每个基因值都用 闭区间 [1, 105] 中的一个整数表示。给你一个下标从 0 开始的整数数组 nums ，其中 nums[i] 是节点 i 的基因值，且基因值 互不相同 。

请你返回一个数组 ans ，长度为 n ，其中 ans[i] 是以节点 i 为根的子树内缺失的最小基因值。

节点 x 为根的子树包含节点 x 和它所有的后代节点。

示例 1：

输入：parents = [-1,0,0,2], nums = [1,2,3,4]
输出：[5,1,1,1]
解释：每个子树答案计算结果如下：
- 0：子树包含节点 [0,1,2,3] ，基因值分别为 [1,2,3,4] 。5 是缺失的最小基因值。
- 1：子树只包含节点 1 ，基因值为 2 。1 是缺失的最小基因值。
- 2：子树包含节点 [2,3] ，基因值分别为 [3,4] 。1 是缺失的最小基因值。
- 3：子树只包含节点 3 ，基因值为 4 。1是缺失的最小基因值。

示例 2：

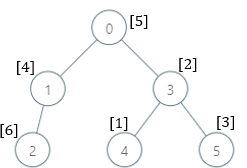
输入：parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3]
输出：[7,1,1,4,2,1]
解释：每个子树答案计算结果如下：
- 0：子树内包含节点 [0,1,2,3,4,5] ，基因值分别为 [5,4,6,2,1,3] 。7 是缺失的最小基因值。
- 1：子树内包含节点 [1,2] ，基因值分别为 [4,6] 。 1 是缺失的最小基因值。
- 2：子树内只包含节点 2 ，基因值为 6 。1 是缺失的最小基因值。
- 3：子树内包含节点 [3,4,5] ，基因值分别为 [2,1,3] 。4 是缺失的最小基因值。
- 4：子树内只包含节点 4 ，基因值为 1 。2 是缺失的最小基因值。
- 5：子树内只包含节点 5 ，基因值为 3 。1 是缺失的最小基因值。

示例 3：

输入：parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8]
输出：[1,1,1,1,1,1,1]
解释：所有子树都缺失基因值 1 。

提示：

n == parents.length == nums.length
2 <= n <= 105
对于 i != 0 ，满足 0 <= parents[i] <= n - 1
parents[0] == -1
parents 表示一棵合法的树。
1 <= nums[i] <= 105
nums[i] 互不相同。

实现代码与解析：

dfs + 启发式合并

class Solution {
public:
    // 邻接表
    vector<int> h = vector<int>(1e5 + 10, -1); vector<int> e = vector<int>(1e5 + 10, 0); vector<int> ne = vector<int>(1e5 + 10, 0);
    int idx = 0;

    void add(int a, int b) {
        e[idx] = b, ne[idx] = h[a], h[a] = idx++;
    }

    vector<int> smallestMissingValueSubtree(vector<int>& parents, vector<int>& nums) {

        int n = parents.size();
        // 存图 加边 邻接表
        for (int i = 1; i < n; i++) { // 这里从1开始，找半天错。。
            add(parents[i], i);
        }

        vector<int> res(n, 1); // 结果数组
        vector<unordered_set<int>> gene(n); // 包含此节点 与 其子树 的基因合集set

        function<int(int)> dfs = [&](int cur) -> int{
            
            gene[cur].insert(nums[cur]); // 当前节点基因值放入

            for (int i = h[cur]; ~i; i = ne[i]) {
                int j = e[i]; // 子节点
                res[cur] = max(res[cur], dfs(j)); // 此节点为根缺失的最小的基因，一定比子树缺失的最小基因大或等于，所以这里取个max
                // 向上传递合集，小的合并到大的效率快，所以先判断（选择是否先交换），在树中属于中序处理
                if (gene[cur].size() < gene[j].size()) {
                    gene[cur].swap(gene[j]);
                }
                gene[cur].merge(gene[j]); // 合并
            }
            
            // 根据res寻找此节点的结果, 一定比子树大或等于，++遍历即可,找到第一个没有的最小基因
            while (gene[cur].count(res[cur]) > 0) {
                res[cur]++;
            }
            return res[cur];
        };

        dfs(0); // dfs
        
        return res;
    }
};