leetCode 137. 只出现一次的数字 II + 位运算 + 模3加法器 + 真值表（数字电路） + 有限状态机

news2024/10/6 20:40:17

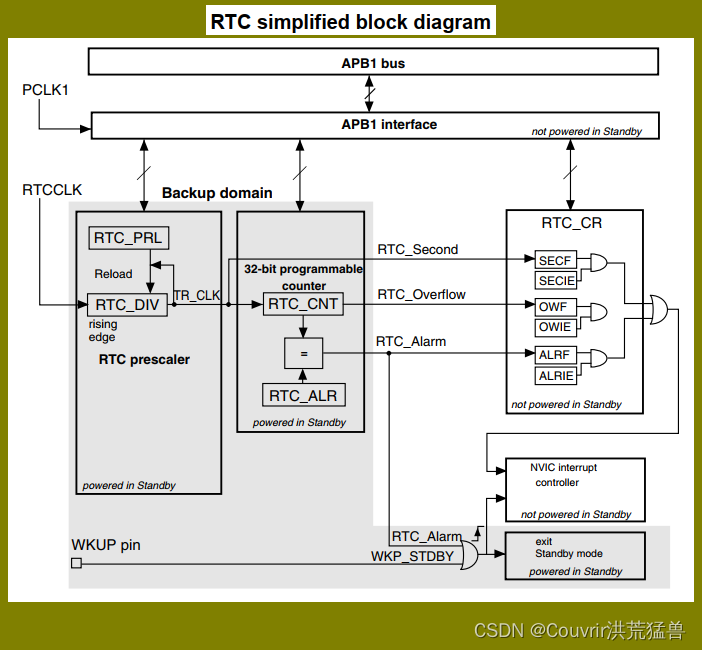
给你一个整数数组 nums ，除某个元素仅出现一次外，其余每个元素都恰出现 三次。请你找出并返回那个只出现了一次的元素。你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。

常规解法：哈希（hash）

使用哈希映射统计数组中每个元素的出现次数，对于哈希映射中的每个键值对，键表示一个元素，值表示其出现的次数。在统计完成后，遍历哈希映射即可找出只出现一次的元素

class Solution {
public:
    // 哈希表
    int singleNumber(vector<int>& nums) {
        unordered_map<int,int> mp;
        for(const int &num:nums) {
            ++mp[num];
        }
        int ans = 0;
        // for(auto &it:mp) 
        //     if(it.second==1) return it.first;
        for(auto [x,cnt]:mp) 
            if(cnt==1) {ans=x;break;}
        return ans;
    }
};

时间复杂度：O(n)，其中 n 是数组的长度。
空间复杂度：O(n)，哈希映射中包含最多 ⌊n/3⌋+1 个元素，即需要的空间为 O(n)

****************************************** 进入本文正题******************************************

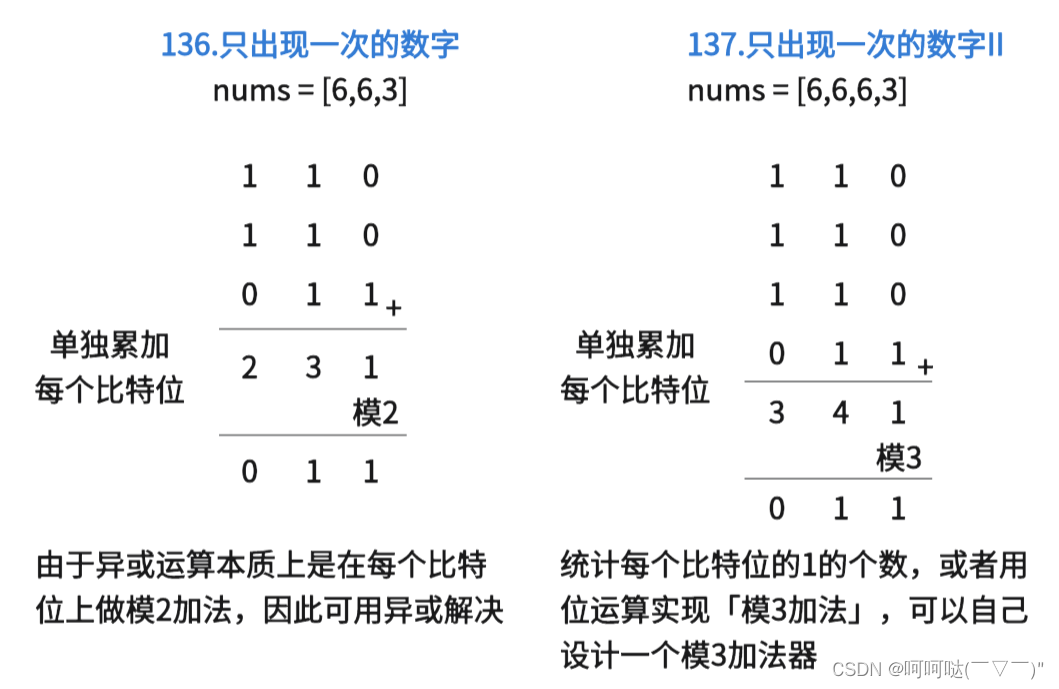
（1）实现「统计每个比特位的 1 的个数」

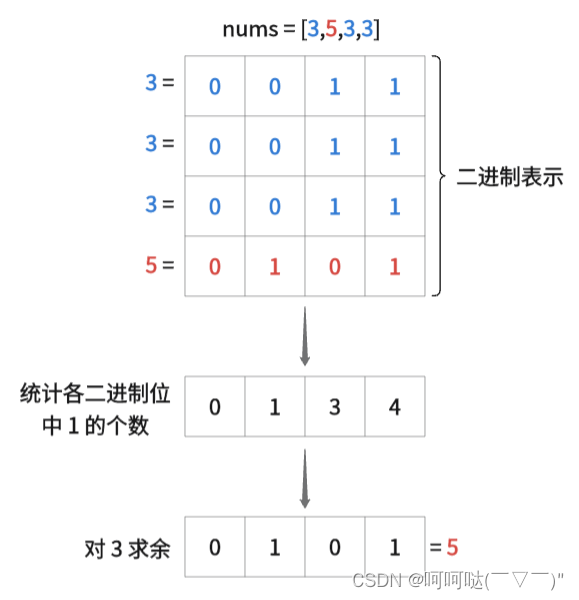
class Solution {
public:
    // 模3加法 方法1：统计每个比特位的1的个数
    int singleNumber(vector<int>& nums) {
        int ans = 0 ;
        for(int i=0;i<32;i++) {
            int cnt = 0;
            for(const int& x : nums) {
                cnt += (x>>i & 1);
            }
            ans |= (cnt%3) << i;
        }
        return ans;
    }
};

（2）位运算，设计 "模3加法器"

可以使用一个「黑盒」存储当前遍历过的所有整数，「黑盒」的第 i 位为{ 0, 1, 2 }三者之一，表示当前遍历过的所有整数的第 i 位之和除以3的余数。但由于二进制表示中只有 0 和 1 而没有 2，因此我们可以考虑在「黑盒」中使用两个整数来进行存储，即：

黑盒中存储了两个整数 a 和 b，且会有三种情况：

a 的第 $i$ 位为 0 且 b 的第 $i$ 位为 0，表示 0
a 的第 $i$ 位为 0 且 b 的第 $i$ 位为 1，表示 1
a 的第 $i$ 位为 1 且 b 的第 $i$ 位为 0，表示 2

当遍历到一个新的整数 $x$ 时，对于 $x$ 的第 $i$ 位 $x_{i}$

如果 $x_{i}$ =0，那么 a 和 b 的第 $i$ 位不变；
如果 $x_{i}$ =1，那么 a 和 b 的第 $i$ 位按照 (00) -> (01) -> (10) -> (00) 这一循环进行变化

分析：本题思路和 single Number 一样，同样考虑一个比特位的情况，这里需要对这个比特进行计数到 3 时归 0，也就是说需要一个模3加法器。但是没有现成的加法器，那么需要自己构造一个能位运算的模3加法器

思考：计数器要经历 0,1,2 这三个状态，但是一个比特位只能表示两个状态，怎么办呢？此时我们可以扩展一个比特，即用两个比特来保存位计数器的三个状态。假设 b 为低位, a 为高位。c 代表 $x_{i}$ （ $x$ 的第 $i$ 位: $x_{i}$ ）用 ab 两个比特位来作为这一位 c 的位计数器。

当这一位 c 来 1 时位计数器就进行状态转换，否则维持原状态，而最后的结果会保存在计算器的低位 b 里
当 c 为 0 时不会变化，那么状态不发生变化

注：a1 和 b1 表示 a，b 的下一个状态 ,c 代表 $x_{i}$ （ $x$ 的第 $i$ 位: $x_{i}$ ）, $a'$ 表示 a非， $b'$ 表示 b非

1.「同时计算」

$a=a' bc+ab'c'$

$b=a'b'c+a'bc'=a'(b'c+bc')$ $=a'(b\bigoplus c)$

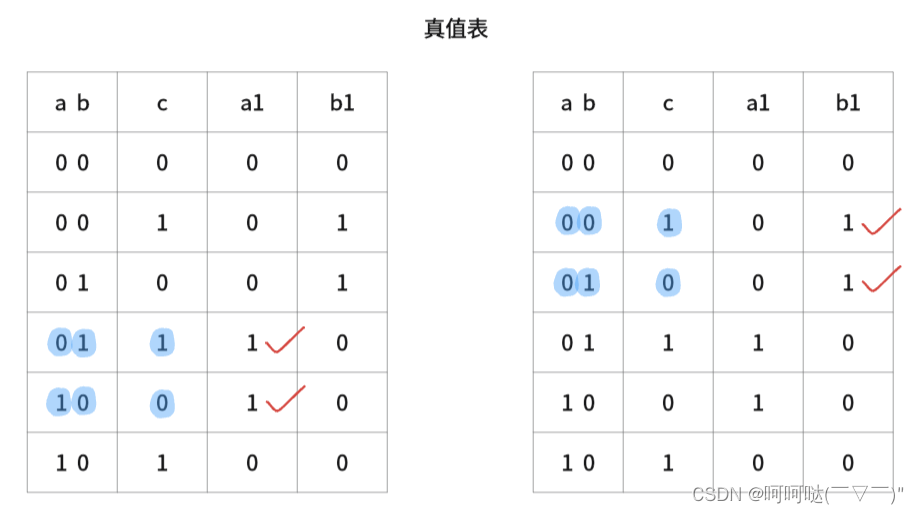
转成代码：

a = (~a & b & c) | (a & ~b & ~c)

b = (~a) & (b ^ c)

C++代码：

class Solution {
public:
    // 模3加法 方法2：用位运算实现
    int singleNumber(vector<int>& nums) {
        int a=0,b=0;
        for(const int& x:nums) {
            int tmp_a = a;
            a = (a^x) & (a|b);
            b = (b^x) & (~tmp_a);
        }
        return b; 
    }
};

2.「分别计算」

发现「同时计算」中计算 b 的规则较为简单，而 a 的规则较为麻烦
可改为「分别计算」，即先计算出 b，再拿新的 b 值计算 a

$b=a'b'c+a'bc'=a'(b'c+bc')$ $=a'(b\bigoplus c)$

$a=a'b'c+ab'c'=b'(a'c+ac')$ $=b'(a\bigoplus c)$

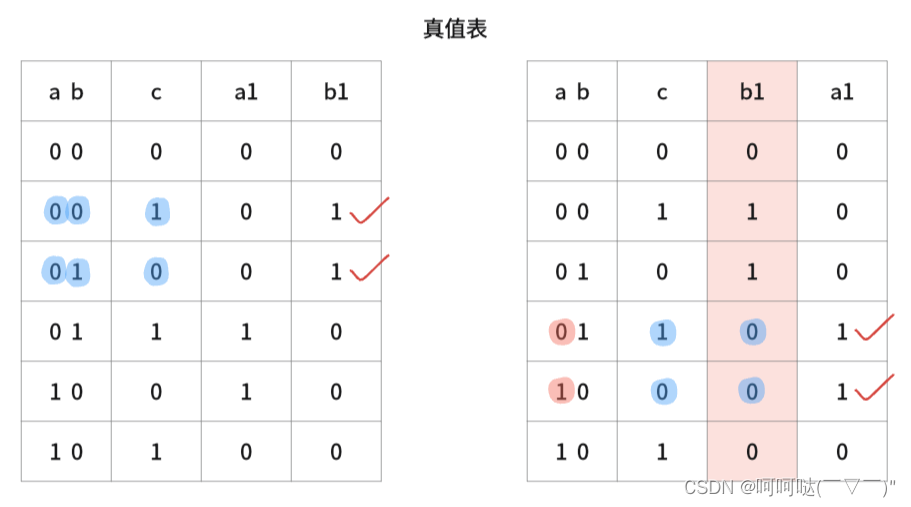
转成代码：

b = (~a) & (b ^ c) // 所以,先计算出b

a = (~b) & (a ^ c) // 再计算a

C++代码：

class Solution {
public:
    // 模3加法 方法2：用位运算实现
    int singleNumber(vector<int>& nums) {
        int a=0,b=0;
        for(const int& x:nums) {
            b = (b^x) & (~a);
            a = (a^x) & (~b);
        }
        return b; 
    }
};

时间复杂度：O(n)，其中 n 为 nums 的长度
空间复杂度：O(1)，仅用到若干额外变量

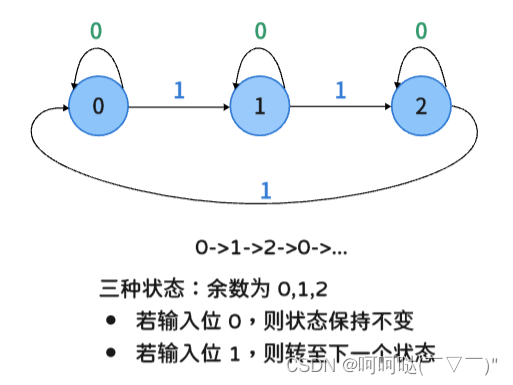
（3）有限状态自动机

对于异或（模2加法）来说，把一个数不断地异或1，相当于在 0 和 1 之间不断转换，即：

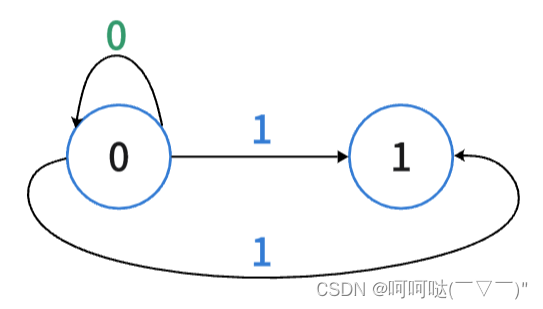
0->1->0->1->...

类似地，模 3 加法 就是在 0, 1, 2, 之间不断转换，即：

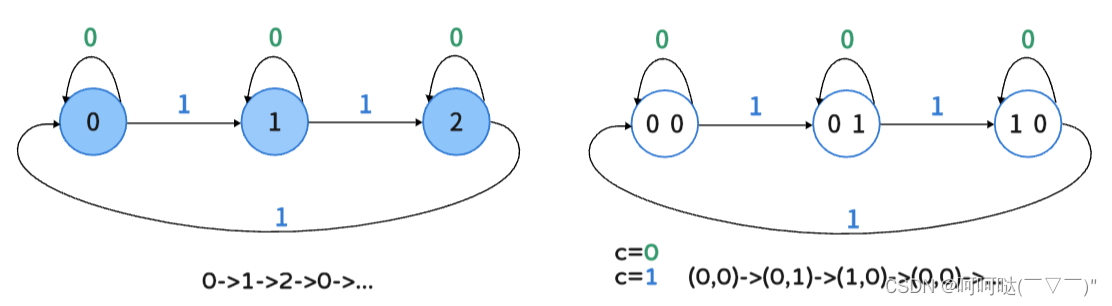
0->1->2->0->1->2->...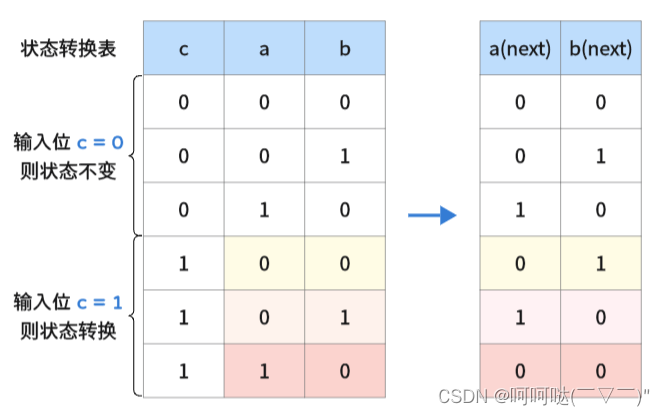

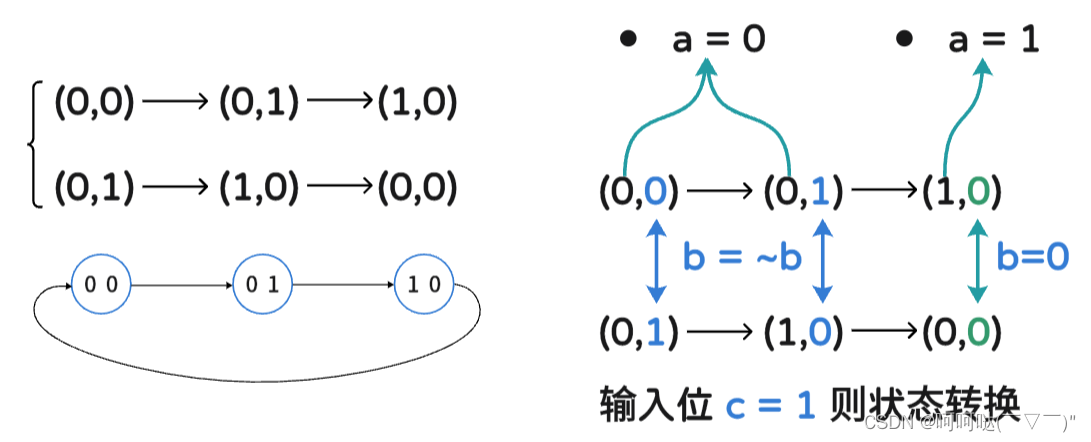
当 a = 0 且 b = 0 时，a 必须保持不变，仍然为 0
当 a = 1 时（此时 b 一定是 0），必须保持不变，仍然为 0

【注】 $c$ 代表 $x_{i}$ （ $x$ 的第 $i$ 位 : $x_{i}$ ）, $a'$ 表示 a非， $b'$ 表示 b非

if(a == 0) {
    if(c == 0) {
        b=b;
    }
    if(c == 1) {
        b=~b;
    }
}

if(a == 1) {
    b=0;
}

引入异或运算，当 if(a == 0) 时，

$b = c'b + cb' = b\oplus c$

转成代码:

if(a == 0) b = b ^ c;

那么可以将上述拆分简化为：

if(a == 0) b = b ^ c;
if(a == 1) b = 0;

引入与运算,继续简化:

$b = a'(b\oplus c)$

转成代码:

b = (~a) & (b ^ c);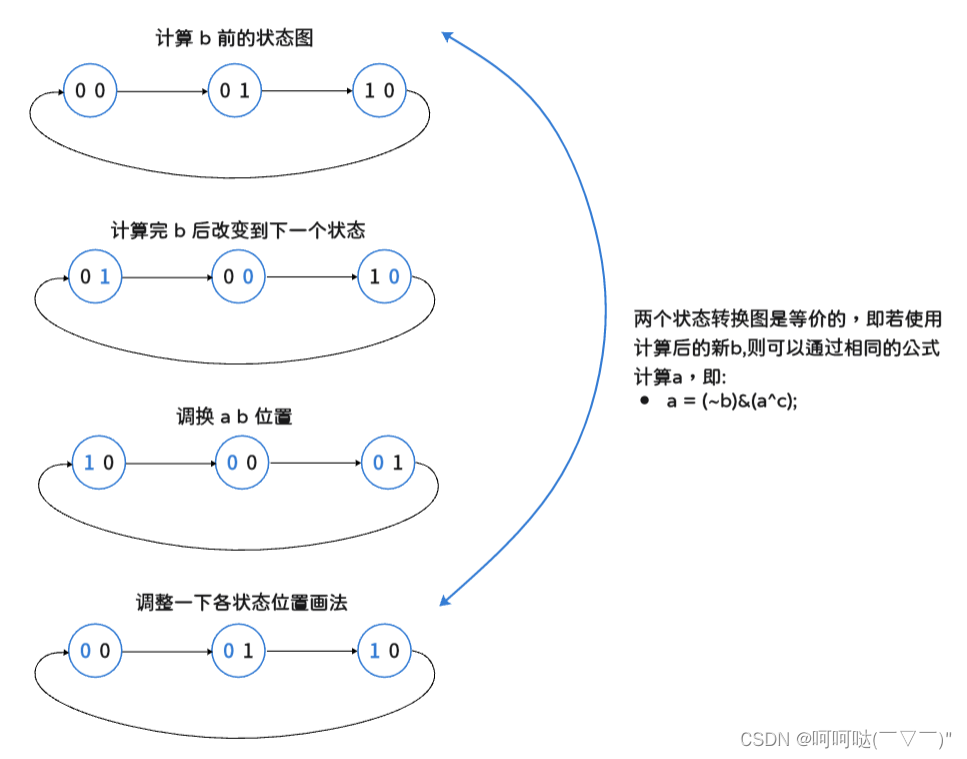

a = (~b) & (a ^ c);

推荐和参考文章：

137. 只出现一次的数字 II - 力扣（LeetCode）https://leetcode.cn/problems/single-number-ii/solutions/2482832/dai-ni-yi-bu-bu-tui-dao-chu-wei-yun-suan-wnwy/137. 只出现一次的数字 II - 力扣（LeetCode）https://leetcode.cn/problems/single-number-ii/solutions/8944/single-number-ii-mo-ni-san-jin-zhi-fa-by-jin407891/137. 只出现一次的数字 II - 力扣（LeetCode）https://leetcode.cn/problems/single-number-ii/solutions/746993/zhi-chu-xian-yi-ci-de-shu-zi-ii-by-leetc-23t6/