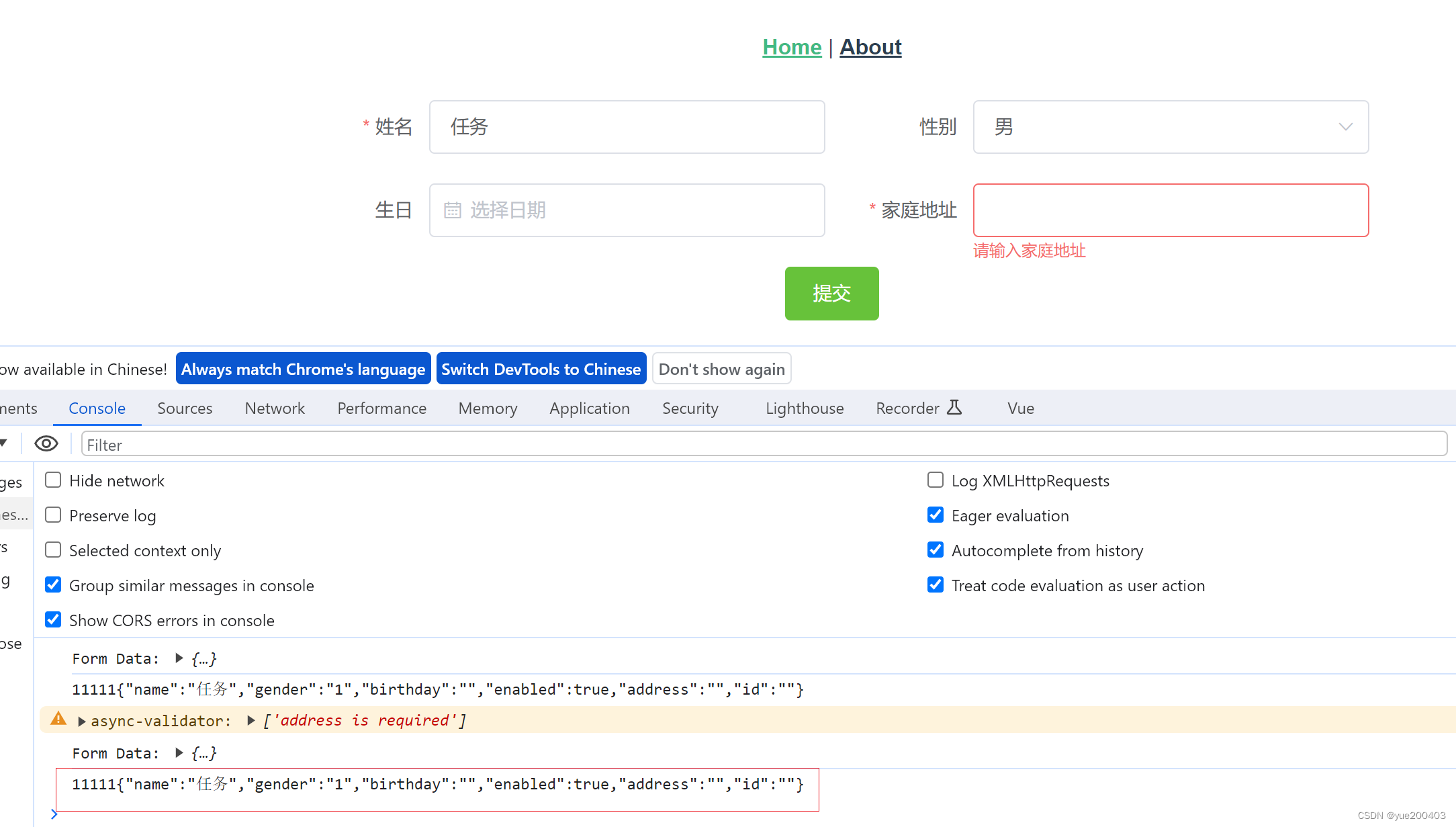
堆是一种特殊的完全二叉树

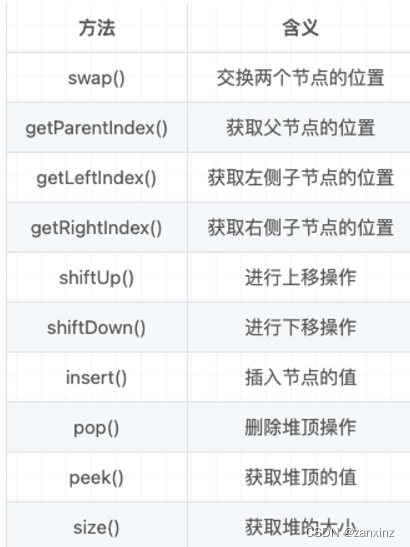
堆具有以下方法

关键点：

1. 插入：在 store 末端插入新元素，然后把新元素上浮。
2. 弹出：将 store 顶端（索引为0处）弹出，作为最小元素；把末端元素放到索引0处，从索引0开始执行下沉操作。

构造最小堆（Python）

class MinHeap:
    def __init__(self):
        self.store = []
        
    def insert(self, ele):
        self.store.append(ele)
        self.shiftUp(self.size() - 1)
    def swap(self, i, j):
        t = self.store[i]
        self.store[i] = self.store[j]
        self.store[j] = t

    def getParent(self, index):
        return (index - 1) // 2

    def shiftUp(self, index):
        if index == 0:
            return
        if self.store[index] < self.store[self.getParent(index)]:
            self.swap(index, self.getParent(index))
            self.shiftUp(self.getParent(index))
    

    def getLeftChild(self, index):
        return index * 2 + 1
    def getRightChild(self, index):
        return index * 2 + 2
    
    def peek(self):
        if self.size() >= 0:
            return self.store[0]
        else:
            return None

    def pop(self):
        if self.size() == 0:
            return None
        if self.size() == 1:
            t = self.store.pop()
            return t
        t = self.store[0]
        
        self.store[0] = self.store.pop()	# move the last one to the place that index == 0
        self.shiftDown(0)
        return t

    def shiftDown(self, index):
        left = self.getLeftChild(index)
        right = self.getRightChild(index)
        if left < self.size() and self.store[index] > self.store[left]:
            self.swap(index, left)
            self.shiftDown(left)
        if right < self.size() and self.store[index] > self.store[right]:
            self.swap(index, right)
            self.shiftDown(right)
    def size(self):
        return len(self.store)

使用最小堆对数组排序

g = [2, 5, 1, 7, 8, 4, 9, 6, 7, 0, 11]

h = MinHeap()
for e in g:
    h.insert(e)

res = []
for i in range(0, len(g)):
    res.append(h.pop())

print(res)