文章信息
论文题目为《IG-Net: An Interaction Graph Network Model for Metro Passenger Flow Forecasting》的一篇2023年4月发表在IEEE TRANSACTIONS ON INTELLIGENT TRANSPORTATION SYSTEMS的地铁客流预测交互图网络模型。
摘要
城市轨道交通系统很大程度上满足了市民的出行需求，缓解了交通拥堵。提高轨道交通的运营效率可以增加轨道交通运营公司的收入和促进城市交通的稳定发展。为实现这一目标，客流预测是轨道交通运营中一项重要的前置工作。然而，客流预测是一项具有挑战性的任务，因为居民出行存在许多不可量化的因素。为了解决这个问题，作者提出了一个名为交互图网络(IG-Net)的创新模型，用于在车站层面进行客流预测，捕捉车站之间的非欧几里得关系。作者设计了三种站间交互图来模拟这些站间交互关系：连通性图、相似性图和时间相关性图。此外，作者应用多通道的图卷积神经网络来捕获交互表示，并开发了跨多站的多任务学习架构。基于苏州地铁数据集的实验，作者提出的IG-Net在预测多个站点的客流时取得了比基准模型更好的性能。最后，作者通过进一步的实验确定了交互图组合和多任务损失函数的显著影响。
介绍
轨道交通作为大都市公共交通的主要支柱，在城市居民的日常出行活动中起着至关重要的作用。因此，准确的客流预测是至关重要的，特别是在确定轨道交通运营效率和服务改进时。然而，交通系统的复杂性和出行者选择的不确定性对准确预测提出了严峻的挑战。对此，智能交通系统(ITS)领域的研究者越来越重视这一问题。客流预测是一种典型的时间序列预测任务，依赖于历史和实时的自动收费(AFC)数据。由于客流的时变性质不是线性关系，检验变量之间的时间相关性是至关重要的。在过去的十年中，许多人致力于预测未来一段时间内的客流，并从最近的时间间隔中获取信息。
由于地铁站提供的出行服务具有互联性，它们之间的相互作用不容忽视。因此，建立车站相互作用的模型有可能提高不同场合客流预测的准确性。然而，很少有研究既分析了地铁站之间的相互作用，又将先验知识应用于客流预测。随着移动网络地图服务的快速发展，大多数人使用地图应用程序进行寻路。因此，网络地图提供的旅行信息对交通决策的影响越来越大。网络地图信息，如旅行时间，可以影响车站之间的相互作用。此外，在同一条地铁线路上的车站之间以及客流具有时间相关性的车站之间存在更显著的相互作用。
基于上述思想，本研究提出了三个交互矩阵，即连通性矩阵、相似性矩阵和时间相关矩阵来表示潜在的相互作用对客流的影响。这些矩阵是基于网络地图数据、地铁网络数据和历史客流数据的地铁站之间潜在相互作用的数值表示，为了有效地利用交互矩阵，提出了一种交互图网络(IG-Net)模型，用于车站层面的客流预测。首先，采用多图卷积神经网络(M-GCNN)通道将交互矩阵纳入历史客流数据的时间序列中，并随历史客流时间变化串联到M-GCNN的输出中，保留原有的客流趋势。其次，将多任务学习(MTL)架构应用于IG-Net的多站客流预测。采用多层感知器(M-TLP)通道对各站点流量进行预测，并考虑自动加权损失(AWL)函数对MTL进行预测。最后，利用苏州地铁系统的AFC数据进行了实验。实验结果表明，结合交互矩阵可以提高地铁客流预测的准确性，最终优于现有的基准方法。综上所述，本研究的贡献有三个方面:
1. 通过连通性矩阵、相似性矩阵和时间相关矩阵来模拟地铁站之间的潜在相互作用。充分考虑车站间的相互作用，捕捉客流特点，应用于不同场合。
2. 将网络地图实时信息纳入地铁客流预测任务。
3. 结合MTL（多任务学习）架构和图卷积神经网络，提出了一种新的神经网络模型IG-Net来预测多站客流。
预备知识
客流预测
客流预测问题是一个典型的时间序列问题，旨在预测基于过去O个时间步的客流观测值，最可能在下一个时间步出现的客流状态。这个问题可以描述为：
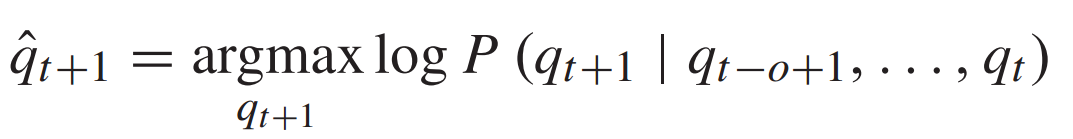
式中，
为第t个时间步N个站点的客流观测量，
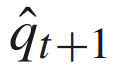为第t+1个时间步的客流估计。
图神经网络
图神经网络，也称为图上的卷积神经网络，是处理由图构成的非欧几里得数据的有效模型。图卷积过程基于图G = (V, E, W)，其中V为节点的集合，E为边的集合，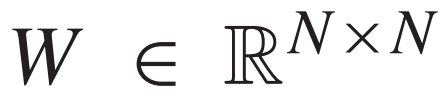
为边的权值。给定图拉普拉斯变换
，其中I为单位矩阵，D为对角度矩阵，通过特征分解得到傅里叶基U，定义为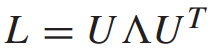
，其中为特征值矩阵。然后将图G上的傅里叶域图卷积过程定义为：
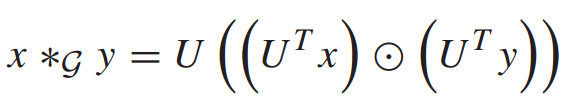
其中x和y是原始信号，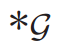
是图卷积算子，
是Hadamard积。在图卷积神经网络中，通常使用傅立叶域中参数化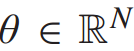
的滤波器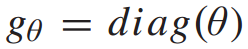
对信号x进行滤波，定义为：
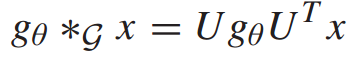
在IG-Net中，使用Chebyshev网络(ChebNet)进行图卷积运算。ChebNet利用参数卷积核对网络进行谱卷积，避免了拉普拉斯矩阵的特征分解。参数核函数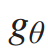
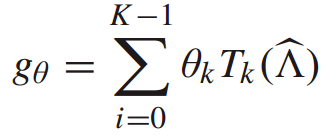
其中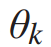
是可训练参数集，
是缩放特征值对角矩阵上K阶的Chebyshev多项式。在该核中，K表示节点仅受其周围K阶邻居节点影响的阶数，并定义缩放后的特征值矩阵
，定义为：
多任务学习
多任务学习已被证明可以在解决多任务问题的同时，在相关任务之间共享表征。因此，由于地铁客流的各个分支可能具有相关的模式和趋势，例如高峰时段的客流，因此它非常适合于预测多个站点的流量。
方法论
站间交互图
1. 连接性图：连接性图Gc是根据站与站之间的走行时间计算的。考虑到车站间的乘客流动，某一车站附近产生的乘客会在一段时间后到达其他车站，造成车站间的客流，同时延迟了车站间的互动。显然，这种客流取决于站与站之间的走行时间。为了确定走行时间，用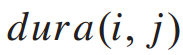
表示站i和站j之间的走行时间。走行时间的值来自于在web地图上查询的信息。此外，步行时间的倒数作为站间连通性强度的度量。为了将Wc的值归一化到0到1的范围内，取λ为站间最短行走时间，即
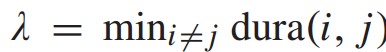。因此，Wc(i, j)的计算公式为：
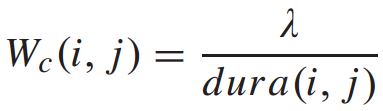
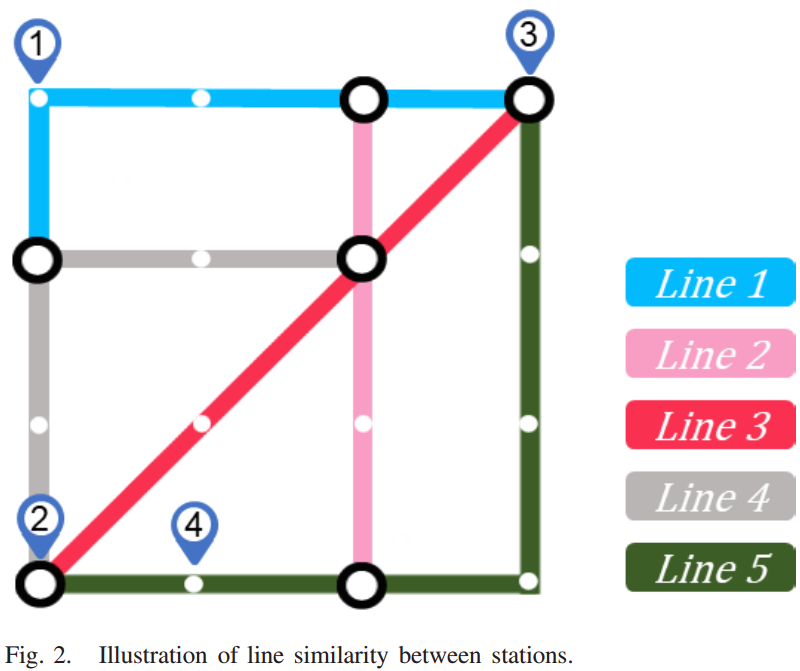
2. 相似性图：相似性图Gs根据站间线路相似度计算。在出行服务市场中，乘客和车站分别是需求者和供给者。提供同类服务的车站之间存在客流竞争，提供不同出行服务的车站之间也存在互补关系。例如，图2中的2号站和4号站是这个区域的竞争对手，因为它们都在3号线上，而且彼此相邻。因此，图2中2号站与3号站的相互作用强于1号站与2号站的相互作用。由于这些车站位于地铁3号线和5号线上，因此在相同的时间间隔内，通勤人数通常会增加。因此，作者使用地铁线路的相似图来捕捉车站间的相互作用，考虑到相邻的站点在同一条线上要有较高的服务相似性。
为了识别相邻站点之间的关系，用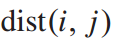
表示站点i与站点j之间的步行距离;我们使用指标函数
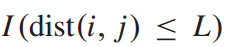表示只有站间距离小于L时服务相似度才显著。与步行时间长度相同，步行距离值来自web地图上查询的信息。更进一步，将连接i站的地铁线路集合记为
。我们利用不同站点之间重叠线与总线的比率来衡量服务相似性。最后，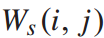
：
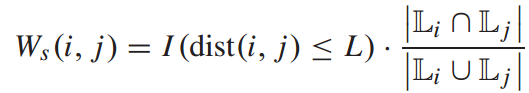
3. 时间相关图：Gt是根据历史客流时间序列构建的，不同车站客流的时间序列相关性受到多种未知因素的影响。通过统计分析计算相关系数是解决这一问题的有效途径。因此，选择历史客流的时间序列相关性来捕捉潜在的相关关系。作者将第i站的时间序列构造为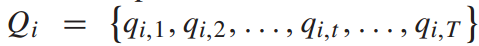
， 综合这些因素，可以得到：
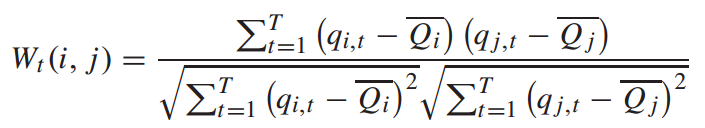
交互图网络
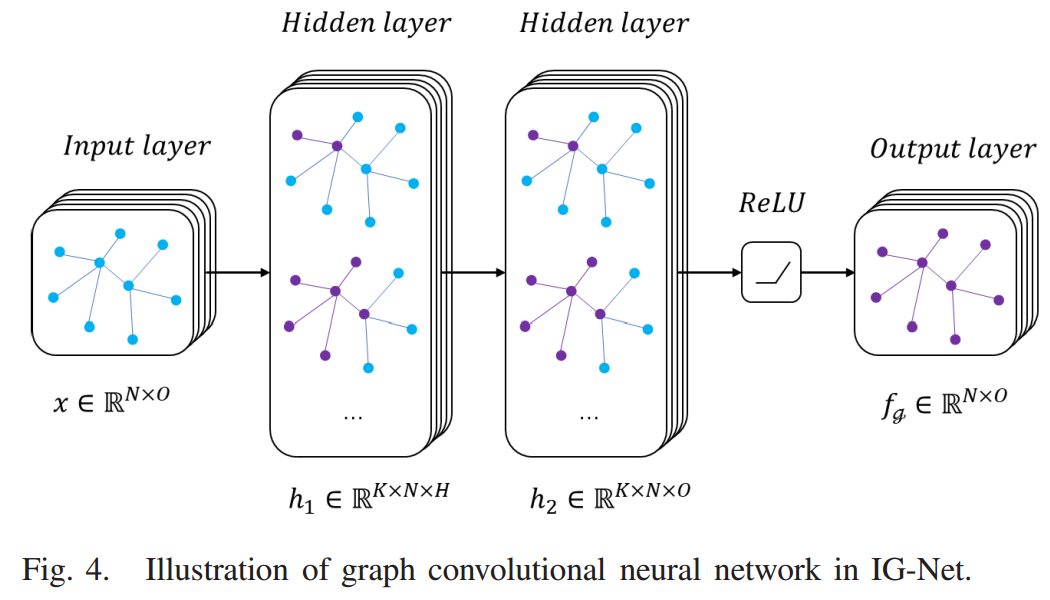
1.多通道图卷积网络：在本节中，我们描述了M-GCNN的结构，并对站间交互图进行了图卷积。M-GCNN是我们模型的前半部分，在接收输入和输出特征矩阵方面起着关键作用。M-GCNN基于不同的站间交互图由三个ChebNet通道组成，如图3所示。如前所述，M-GCNN模块用于将交互矩阵合并到历史客流时间序列中，并捕获隐藏在站间交互图中的交互表示。
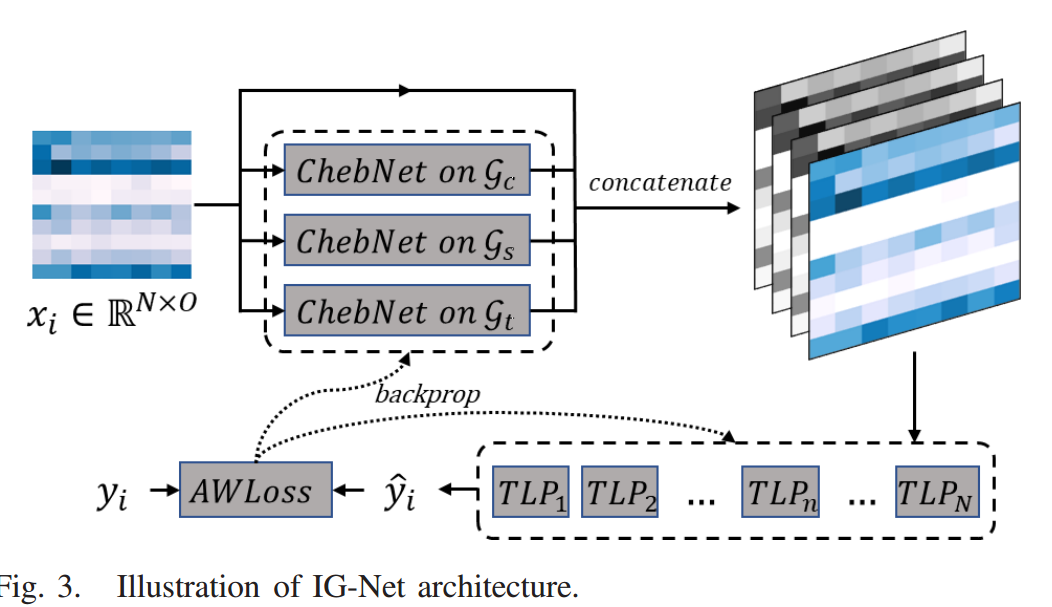
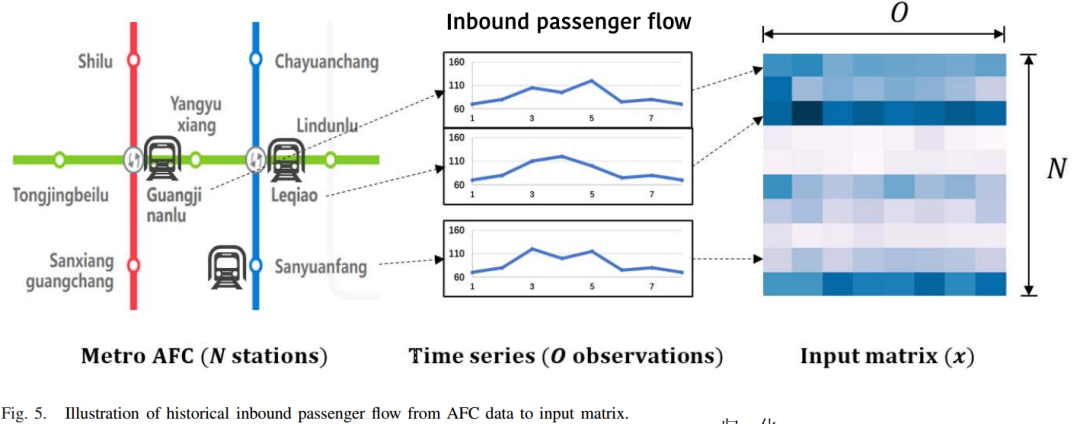
ChebNet的一个通道有两个图卷积操作步骤，如图4所示。M-GCNN的输入矩阵为历史客流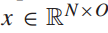
，如图5所示，其中N为站点数，O为历史观测次数。隐藏层的特征维数分别为H和O。交互表示是输出
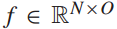。ChebNet过程的一个通道可表示为:
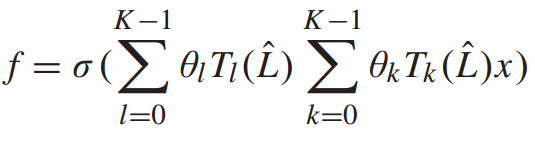
其中σ为非线性激活函数。考虑到ReLU计算简单，训练效率高，本文选择ReLU作为激活函数，可以表示为:
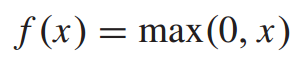
2. 多任务学习结构：为了提高多车站的客流预测精度，IG-Net受到了MTL模式架构的启发，一个站点的流量预测任务对应于一个单任务分支。M-GCNN是IG-Net中实现共享表示的共享层。经过M-GCNN，产生了三种交互表示，包含了站间潜在的交互。此外，我们将历史客流与交互表示连接起来构建特征张量F，式为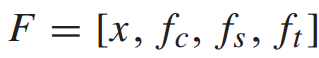
，其中
。
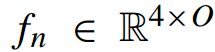张量根据站点n包含各种特征。为了准确拟合目标与各种特征之间的函数，由于两层感知器(two-layer perceptron, TLP)具有强大的拟合能力，因此采用TLP进行拟合和预测任务。
除了多个两层感知器之外，AWL函数也是MTL的重要组成部分。在MTL中，每个任务τ∈T都有损失函数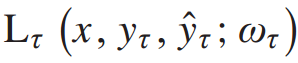
，其中
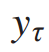和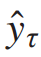
分别表示任务τ的目标值和估计值，
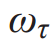表示任务τ中的可学习参数。更重要的是，利用加权因子
来组合多个损失函数，以学习各种任务的自适应权重。在我们的工作中，我们采用了多任务损失函数，
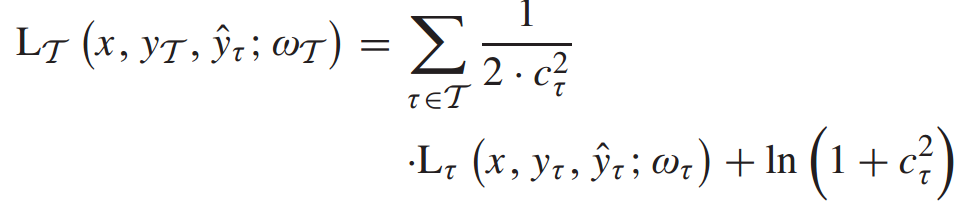
其中，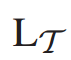
表示所有任务的损失，加权项
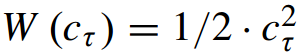和正则化项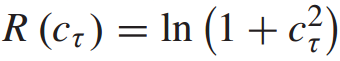
，分别用于执行正加权和正则化值。
实验
实验细节
1. 本文使用来自中国苏州的地铁AFC数据，数据集中包含2018年8月1日至2018年9月30日所有刷卡数据，每条AFC数据包含卡ID、卡类型、站点ID、站点名称、时间戳等字段。当时，苏州地铁系统有93个车站和4条线路。如图所示，8月10日的车站客流面图显示了相似客流高峰时数的车站之间相似的客流趋势。
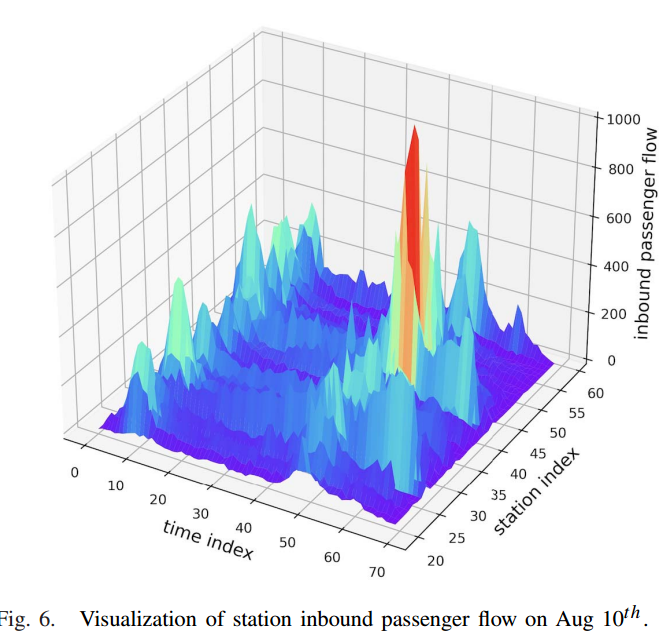
本研究使用的客流数据为进站数据。我们首先将每天划分为96个15分钟的时间间隔，这是交通流领域中常用的时间粒度。然后,我们将每个车站每个间隔的智能卡记录整合为车站的客流。此外，我们保留了地铁运营时间的客流数据，并删除了非运营时间的数据。接下来，我们选取8个观测值来构建数据集，即所有站点过去8个时间间隔的客流形成输入x，所有站点下一个时间间隔的输出形成输出y。最后，按照6:2:2的比例将数据集划分为训练数据集、验证数据集和测试数据集。我们还利用网络地图上的线-站对信息、步行距离和站间步行时间来计算站间交互矩阵。步行距离和持续时间是从高德地图API中抓取的，并转换为类似于起点-目的地矩阵的站-站对格式
2. 数据标准化：我们采用均值归一化对各车站客流进行量化，因为它加速了梯度下降收敛，正则化系数被适当地惩罚。
3. 评估指标：本文采用均方根误差(RMSE)、平均绝对误差(MAE)和R-Squared (R2)来评估IG-Net的准确性和拟合质量，计算公式如下所示：
4. 实验设置：实验中，IG-Net的超参数包括批次大小、学习率、训练次数、两层感知器中隐藏单元的个数和ChebNet的阶数K。通过网格搜索[4, 8, 16, 32]选择批次大小为8。设置初始学习率为0.1，学习率衰减因子为每200次0.1。训练次数设置为1000。将隐藏单位的数量设置为16。ChebNet的阶数K是IG-Net的一个重要参数，根据在验证数据集上的性能，通过网格搜索从集合[1, 2, 3, 4, 5]中选择。选取的K值为3。
基准模型
在本节中，作者将提出的模型(IG-Net)与五种适用于多站点客流预测的经典模型进行了比较。分别为：①历史平均模型(HA)；②多通道神经网络(M-NN)；③图卷积神经网络(GCNN)；④时间图卷积网络(T-GCN)；⑤物理-虚拟协作图网络(PVGCN)。
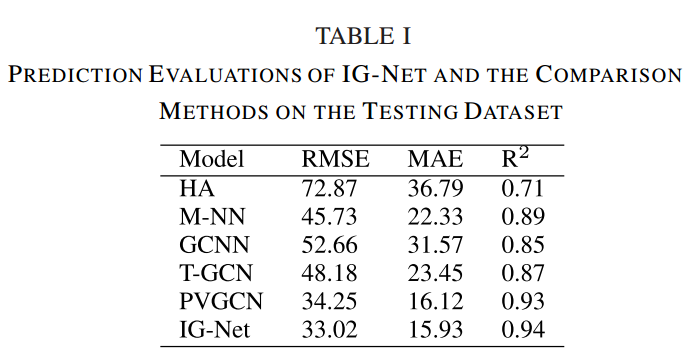
在实验数据集上，作者将所提出的模型IG-Net与其他模型进行了比较。为了比较不同角度的客流预测效果，计算了误差指标RMSE和MAE，以及拟合优度R2。表1显示了所有方法的RMSE、MAE和R2。基线HA的拟合性能不理想，R2为0.71。GCNN和T-GCN的性能明显优于HA；M-NN模型获得了第三好的性能，因为M-NN具有多任务学习架构，可以通过依赖的两层感知器预测每个站点的客流。PVGCN模型的性能优于上述模型，RMSE为34.25。我们提出的模型IG-Net在所有三个评估指标上都取得了最好的表现，RMSE为33.02，MAE为15.93，R2为0.94。需要注意的是，使用基于站间交互图的辅助M-GCNN模块，IG-Net的性能优于M-NN。该模型验证了交互图预测多站客流的有效性。
消融实验
1. 交互图分析：我们使用不同的图组合生成了IG-Net模型的多个变体来分析交互图的影响，不同的模型通过标识符(如G1、G12等)来区分。变体名称对应关系和图形组合如表2所示。注意*表示没有使用任何图形。变体模型分为无图模型、单图模型、双图模型和三图模型。单图模型G1、G2、G3均优于G0，说明交互图具有正向作用，提高了预测精度。有趣的是，改善的顺序随着G3、G2和G1而下降。这个顺序说明了时间相关图Gt比连接图和时间相关图更能提高预测精度，这在双图模型比较中再次得到验证。在双图模型中，G23的表现优于其他双图模型和单图模型。这意味着相似性图和时间相关图的结合可以有效地协同提高多个站点的客流预测。然而，G12的表现甚至不如G3，即时间单图模型，再次验证了时间相关图数据的重要性。最后，对应于完整图特征Gc、Gs和Gt的IG-Net达到了最佳的性能。虽然G23和IG-Net的R2值非常接近，但IG-Net的RMSE和MAE分别降低了3%和0.8%。这意味着IG-Net可以在客流预测任务上获得更好的拟合度。
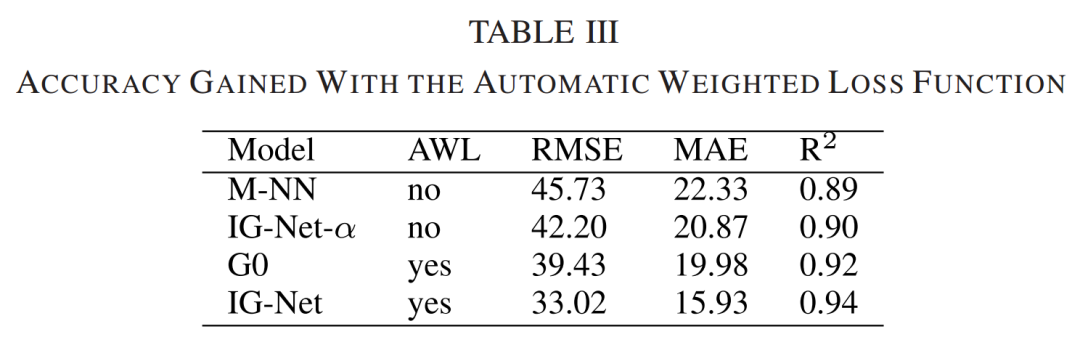
2. 损失函数分析：为了评价AWL函数的有效性，作者设置了两组对照实验。一组包括M-NN和G0，因为它们具有相似的模型结构，不同之处在于是否使用AWL。另一组包括IG-Net和IG-Net-α(不含AWL的IG-Net版本)，实验结果如表3所示。使用AWL的模型比不使用AWL的模型表现更好，R2从0.03提高到0.04，RMSE和MAE也显著降低，说明AWL函数在一定程度上提高了客流预测的精度。一种合理的解释是，AWL函数可以学习平衡各种损失，从而获得比单独学习每个任务更好的性能。
结论
本文作者提出了一种基于IG-Net的车站客流预测方法。为了捕捉车站间的非欧几里得关系，设计了三种图来充分提取车站间的相互作用：连通性图、相似性图和时间相关图。此外，作者设计了一种新的基于深度学习的模型来提取所设计的交互图特征，并将多任务学习架构应用于多站客流预测，该模型利用M-GCNN（多图卷积神经网络）捕获交互表示。此外，作者通过苏州地铁AFC数据的实验来评估所提出模型的性能。实验结果表明，该模型的性能优于基准模型。最后，作者验证了交互图组合和AWL函数对多站客流预测的影响，确定AWL和交互图显著提高了模型的有效性。本文作者尝试利用车站间交互图和网络地图信息对客流进行预测。在未来的研究中，值得考虑使用图卷积神经网络对进站乘客和出站乘客之间的站间交互进行建模，因为存在许多潜在的交互。例如，通勤地铁线路站点的入站客流会直接影响通勤地铁其他站点的出站客流。此外，网络地图信息中的更多功能将应用于预测客流，例如推荐路径。此外，作者将尝试建立基于空间熵的空间多样性模型，以进一步考虑地铁网络的随机性和空间多样性。
