堆排序是一种利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
需要注意的是排升序要建大堆,排降序建小堆。
堆排序的基本思想是:将待排序的序列构造成一个大顶堆(或小顶堆),然后将堆顶元素与最后一个元素交换,然后对剩下的元素重新调整为大顶堆(或小顶堆),如此反复进行,直到序列完全有序。如下图所示:
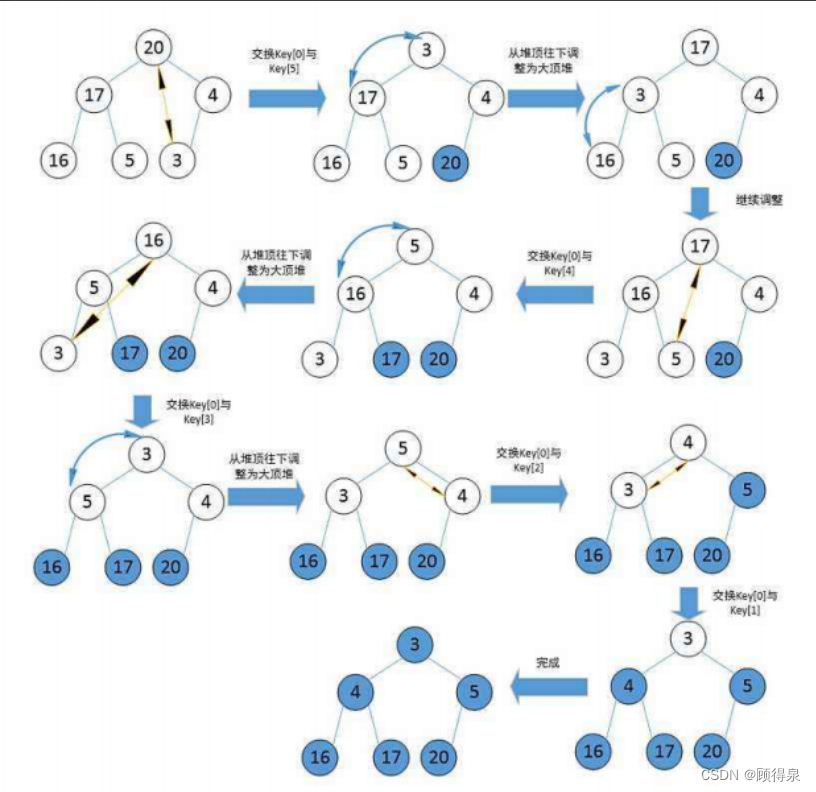
具体代码实现如下:
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
首先定义了一个AdjustDown函数,用于调整堆中的元素位置。该函数接受一个整数数组a、数组长度n和父节点索引parent作为参数。在函数内部,首先计算左子节点的索引child,然后通过循环不断比较当前节点与左右子节点的大小,如果当前节点小于子节点,则交换它们的位置,并更新父节点索引和子节点索引,继续向下调整。
void HeapSort(int* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
} 接下来定义了HeapSort函数,用于对整个数组进行堆排序。该函数接受一个整数数组a和数组长度n作为参数。在函数内部,首先通过循环调用AdjustDown函数将整个数组构建成一个大顶堆,然后从最后一个元素开始,将其与堆顶元素交换,并调用AdjustDown函数调整剩余元素的位置,直到所有元素都被排序。
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
} 这段代码用于打印一个整数数组。它接受两个参数:一个指向整数数组的指针a和一个整数n,表示数组的长度。函数内部使用了一个循环来遍历数组中的每个元素。在每次迭代中,它将当前元素的值通过printf函数打印出来,并在每个元素之间添加一个空格。最后,在循环结束后,它再次调用printf函数打印一个换行符,以便在输出中分隔不同的数组元素。
void TestHeapSort()
{
int a[] = { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 };
HeapSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}这段代码是一个测试函数,用于测试堆排序算法。它首先定义了一个整数数组a,然后调用HeapSort函数对数组进行堆排序,最后调用PrintArray函数打印排序后的数组。
整体实现结果如下:
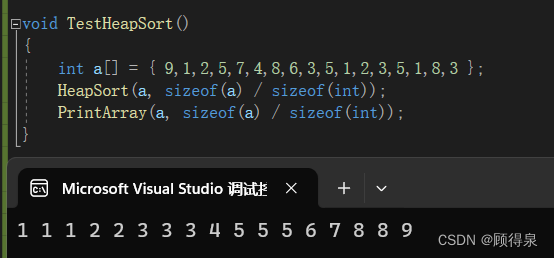
结语:堆排序的分享到这里就结束了,希望对大家的学习会有帮助,如果大家有什么问题或者不同的见解,欢迎大家的留言~~~