一、介绍

        考虑下面的图像，它具有两种数据类型，红色和蓝色。我们找到一条线f(x)=ax1+bx2+cf(x)=ax1+bx2+c，它将两条数据都分为两个区域。当我们得到一个新的test_data XX时，只需将其替换为f(x)f(x)即可。如果f(X)>0f(X)>0，则属于蓝色组，否则属于红色组。我们可以将此行称为“决策边界”。它非常简单且内存高效。可以将这些数据用直线（或高维超平面）一分为二的数据称为**线性可分离**数据。

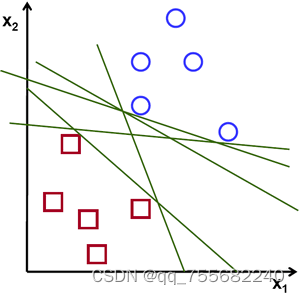
        因此，在上图中，你可以看到很多这样的行都是可能的。我们会选哪一个？非常直观地，我们可以说直线应该从所有点尽可能远地经过。为什么？因为传入的数据中可能会有噪音。此数据不应影响分类准确性。因此，走最远的分离线将提供更大的抗干扰能力。因此，SVM要做的是找到到训练样本的最小距离最大的直线（或超平面）。请参阅下面图像中穿过中心的粗线。

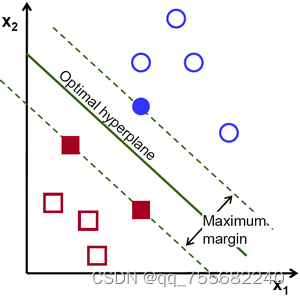
        因此，要找到此决策边界，你需要训练数据。那么需要全部吗？并不用。仅接近相反组的那些就足够了。在我们的图像中，它们是一个蓝色填充的圆圈和两个红色填充的正方形。我们可以称其为**支撑向量**，通过它们的线称为**支撑平面**。它们足以找到我们的决策边界。我