激光雷达点云处理在五年前就做了较多的工作,最近有一些新的接触发现激光雷达代码原理五年前未见重大更新,或许C++与激光雷达结合本身就是比较高的技术门槛。深度学习调包侠在硬核激光雷达技术面前可以说是完全的自愧不如啊。
1、点云滤波
在获取点云数据时,由于设备精度、操作者经验、环境因素等带来的影响,点云数据中将不可避免地出现一些噪声点。而滤波的作用就是利用数据的低频特性剔除离群数据,并进行数据平滑或者提取特定频段特征。
对应的问题是什么时候需要做点云滤波?大概可以分为以下四个方面:1、点云数据密度不规则需要平滑;2、因为遮挡等问题造成离群点需要去除;3、大量数据需要进行下采样;4、噪音数据需要去除。
1.1 常用的点云滤波器:
-
直通滤波器 条件滤波器
-
高斯滤波器 双边滤波器 统计滤波器 半径滤波器 频率滤波器
-
体素滤波器
从功能层面以上点云滤波器可以分为三类使用:直通和条件滤波用于预处理的最前端提取出感兴趣区域;体素滤波用于对密集点云进行下采样减少数据量;其他滤波器用于平滑点云同时去除离散点。
1.2 点云滤波器介绍:
- 直通滤波器
原理:在点云的指定维度上设置一个阈值范围,将这个维度上的数据分为在阈值范围内与不在阈值范围内,从而选择过滤与否。能够快速过滤掉用户自定义区间范围内的点云。
在实际应用中,由于激光扫描采集的距离较远,但是根据功能需求的不同可能只关心一定区域内的数据,比如低速物流车的运营场景,可能在X方向只关心前后60米,Y方向只关心左右20米的范围。此时就可以利用直通滤波器提取出感兴趣区域,可较快剔除部分点云,达到第一步粗处理的目的。
- 条件滤波器
原理:通过设定滤波条件进行滤波,类似于分段函数,判断点云是否在规则的范围则中,如果不在则舍弃。上述的直通滤波器就是一种较简单的条件滤波器。
- 高斯滤波器
原理:采用加权平均方式的一种非线性滤波器,在指定域内的权重是根据欧式距离的高斯分布,通过权重加权平均的方式得到当前点的滤波后的点。
特点:利用标准差去噪,适用于呈正态分布的数据平滑效果较好,但是边缘角点也会被较大的平滑。
- 双边滤波器
原理:通过取邻近采样点的加权平均来修正当前采样点的位置,在高斯滤波器只考虑空间域点的位置基础上,增加了维度上的权重。一定程度上弥补了高斯滤波的缺点。
特点:既有效地对空间三维模型表面进行降噪,又可以保持点云数据中的几何特征信息,避免三维点云数据被过渡光滑。但是只适用于有序点云。关于高斯滤波和双边滤波,本身在图像领域其实已经有广泛的应用,具体的算法原理可以参考保边滤波–bilateral filter and guided filter
。
- 体素滤波器
原理:通过对输入的点云数据创建一个三维体素栅格,然后在每个体素内,用体素中所有点的重心来近似显示体素中的其他点,这样该体素内所有点就用一个重心点最终表示。也有另外一种相似的表达形式:利用每一个体素立方体的中心来近似该体素立方体内的所有点,相比上一种方法计算速度较快,但是损失了原始点云局部形态的精细度。
特点:可以达到向下采样同时不破坏点云本身几何结构的功能。点云几何结构不仅是宏观的几何外形,也包括其微观的排列方式,比如横向相似的尺寸,纵向相同的距离。随机下采样虽然效率比体素网格滤波器高,但会破坏点云微观结构。
以上几种滤波器不会针对离散群点做相关操作,但是实际上离散群点这类噪声点会对整体算法带来比较严重的干扰。离散群点会破坏点云的表达准确性。使得局部点云特征(例如表面法线或曲率变化)的估计变得非常复杂,这往往导致错误的估计结果,从而可能导致点云配准失败。
- 统计滤波器
原理:对每个点的邻域进行一个统计分析,并修剪掉那些不符合一定标准的点。我们的稀疏离群点移除方法基于在输入数据中对点到临近点的距离分布的计算。
具体方法如下:计算每个点到其最近的k个点平均距离,(假设得到的结果是一个高斯分布,其形状是由均值和标准差决定),那么平均距离在标准范围之外的点,可以被定义为离群点并从数据中去除。
特点:主要是根据密度去除离群点,对密度差异较大的离群点去除效果较好。
- 半径滤波器
原理:与统计滤波器类似,只是操作更加暴力直观,根据空间点半径范围临近点数量来滤波。
具体方法如下:
在点云数据中以某点为中心画一个圆计算落在该圆中点的数量,当数量大于给定值时,则保留该点,数量小于给定值则剔除该点。此算法运行速度快,依序迭代留下的点一定是最密集的,但是圆的半径和圆内点的数目都需要人工指定。
特点:用于去除离群点,在一定程度上可以用来筛选边缘点。

- 频率滤波器
原理:在点云处理中,点云法线向量差为点云所表达的信号。用点云的曲率来表示频率信息,如果某处点云曲率大,则点云表达的是一个变化高频的信号。如果点云曲率小,则点云表达的是一个不变低频的信号。例如:地面曲率小,它表达的信息量也小;障碍物处曲率大,频率就会更高。
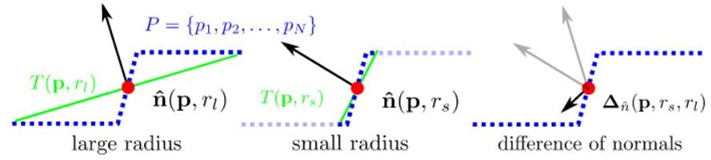
以DoN算法为例,根据不同尺度下法向量特征的差异性,利用pcl::DifferenceOfNormalsEstimation实现点云分割,在处理有较大尺度变化的场景点云分割效果较好,利用不同支撑半径去估算同一点的两个单位法向量,单位法向量的差定义DoN特征。具体如下:在小尺度上计算点云法线1,在大尺度上计算点云法线2,法线1-法线2,滤去3中值较小的点,根据第三步得到的法线差,进行欧式分割。
特点:在小尺度上是可以对高频信息进行检测的,可以很好的小尺度高频信息。其在大规模点云中优势尤其明显。
DoN特征源于观察到基于所给半径估计的表面法向量可以反映曲面的内在几何特征,因此这种分割算法是基于法线估计的,需要计算点云中某一点的法线估计。而通常在计算法线估计的时候都会用到邻域信息,很明显邻域大小的选取会影响法线估计的结果。
而在DoN算法中,邻域选择的大小就被称为support radius。对点云中某一点选取不同的支持半径,即可以得到不同的法线估计,而法线之间的差异,就是是所说的法线差异。