LeetCode169——多数元素（众数）

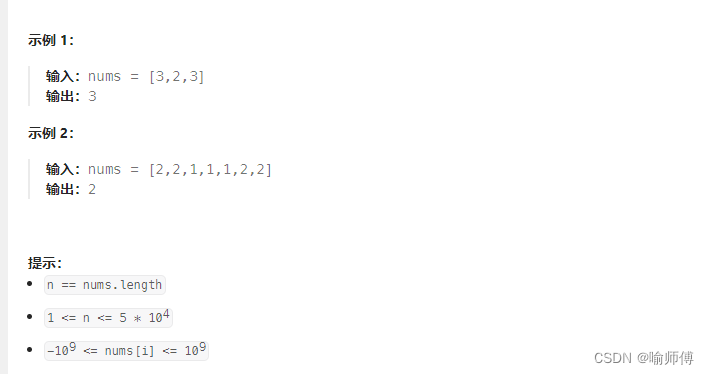
给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

Result01（排序）

将数组进行排序，排序后的中间元素一定是多数元素。因为多数元素出现的次数大于 ⌊ n/2 ⌋，所以排序后的中间元素一定是多数元素。

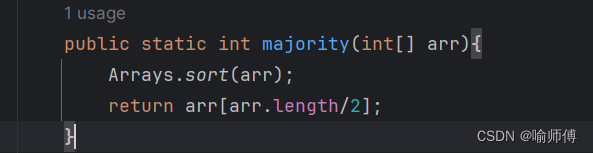
时间复杂度取决于排序算法的复杂度，空间复杂度取决于排序算法所用的栈空间;
若快排则时间为O（nlogn），空间（使用的栈空间）为O(logn)。

Result02（哈希表计数法）

遍历数组，使用哈希表来记录每个元素出现的次数。当某个元素的出现次数超过 ⌊ n/2 ⌋ 时，即可返回该元素作为多数元素。

时间复杂度：O（N）；空间复杂度：O（N）。

/*
    思路:
    我们知道出现次数最多的元素大于 ⌊n/2⌋次，所以可以用哈希表来快速统计每个元素出现的次数。
    算法:
    我们使用哈希映射（HashMap）来存储每个元素以及出现的次数。对于哈希映射中的每个键值对，键表示一个元素，值表示该元素出现的次数。

    我们用一个循环遍历数组 nums 并将数组中的每个元素加入哈希映射中。在这之后，我们遍历哈希映射中的所有键值对，返回值最大的键。我们同样也可以在遍历数组 nums 时候使用打擂台的方法，维护最大的值，这样省去了最后对哈希映射的遍历。*/
    
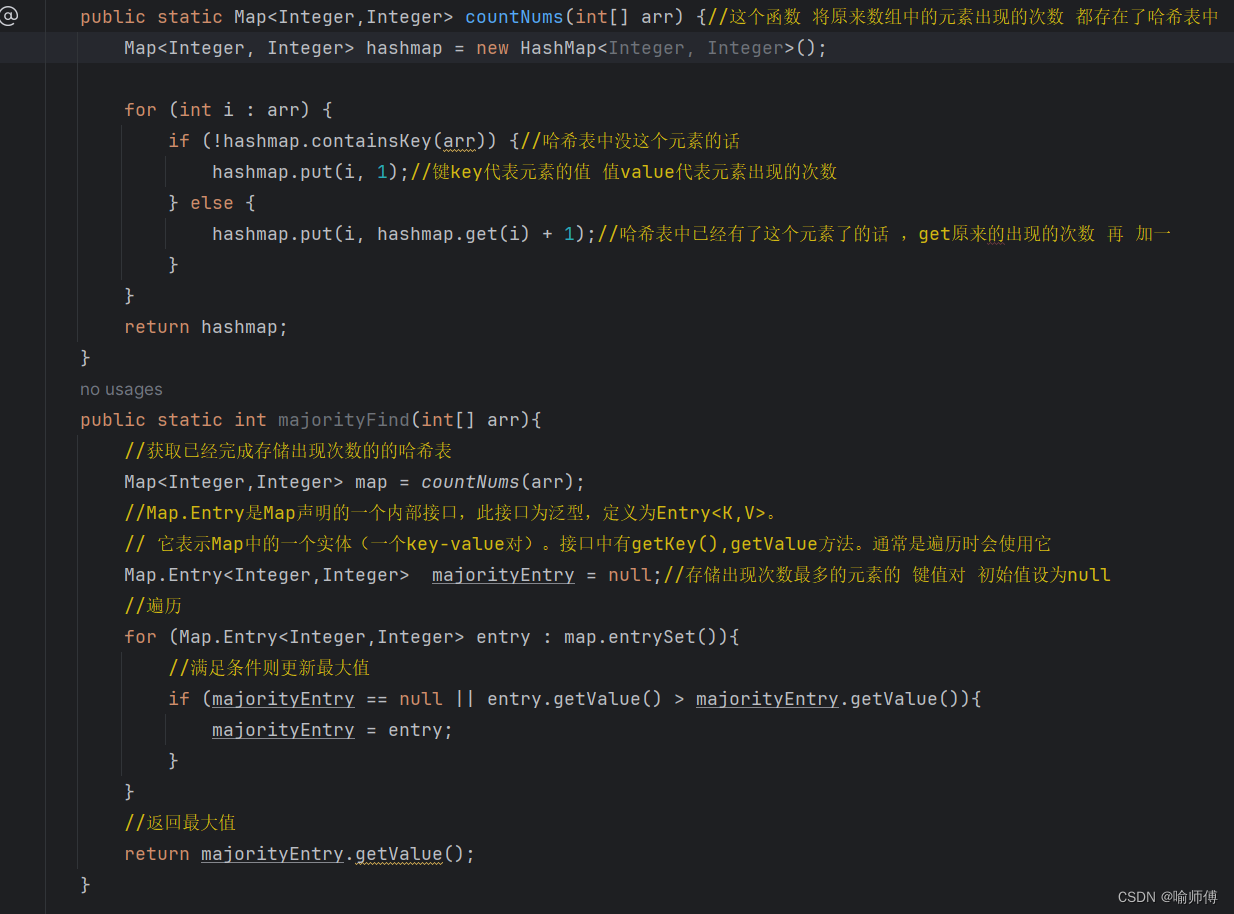
  public static Map<Integer,Integer> countNums(int[] arr) {//这个函数 将原来数组中的元素出现的次数 都存在了哈希表中
        Map<Integer, Integer> hashmap = new HashMap<Integer, Integer>();

        for (int i : arr) {
            if (!hashmap.containsKey(arr)) {//哈希表中没这个元素的话
                hashmap.put(i, 1);//键key代表元素的值 值value代表元素出现的次数
            } else {
                hashmap.put(i, hashmap.get(i) + 1);//哈希表中已经有了这个元素了的话 ，get原来的出现的次数 再 加一
            }
        }
        return hashmap;
    }
    public static int majorityFind(int[] arr){
        //获取已经完成存储出现次数的的哈希表
        Map<Integer,Integer> map = countNums(arr);
        //Map.Entry是Map声明的一个内部接口，此接口为泛型，定义为Entry<K,V>。
        // 它表示Map中的一个实体（一个key-value对）。接口中有getKey(),getValue方法。通常是遍历时会使用它
        Map.Entry<Integer,Integer>  majorityEntry = null;//存储出现次数最多的元素的 键值对 初始值设为null
        //遍历
        for (Map.Entry<Integer,Integer> entry : map.entrySet()){
            //满足条件则更新最大值
            if (majorityEntry == null || entry.getValue() > majorityEntry.getValue()){
                majorityEntry = entry;
            }
        }
        //返回最大值
        return majorityEntry.getValue();
    }

Result03(摩尔投票法Boyer-Moore Voting Algorithm)

核心思想是：“对拼消耗”
假设第一个元素是多数元素，然后遍历数组，对于当前元素，如果与候选多数元素相同，则计数器加1，如果与候选多数元素不同，则计数器减1。当计数器减为0时，将当前元素设为新的候选多数元素，并重置计数器。最终留下的候选多数元素就是答案。

时间复杂度O(N)，空间复杂度O（1）。

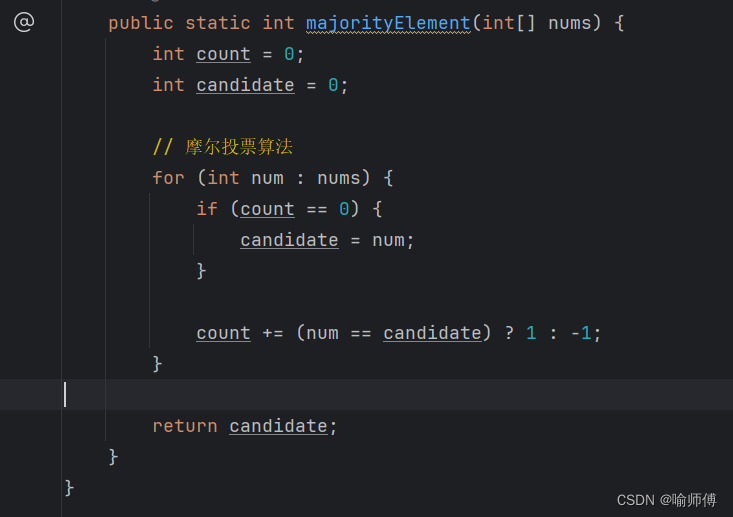
public static int majorityElement(int[] nums) {
        int count = 0;
        int candidate = 0;

        // 摩尔投票算法
        for (int num : nums) {
            if (count == 0) {
                candidate = num;
            }

            count += (num == candidate) ? 1 : -1;
        }

        return candidate;
    }