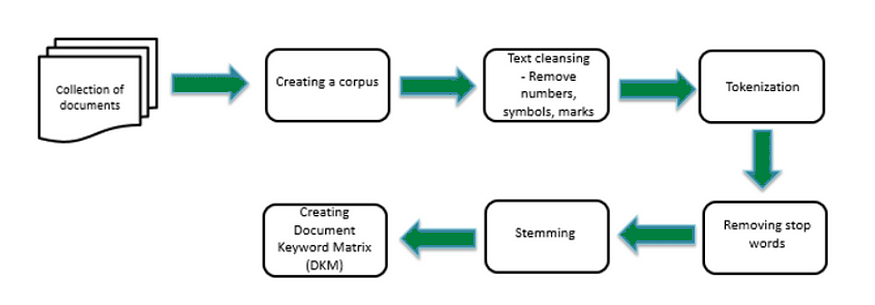
一、简介

装饰器模式主要解决继承关系过于复杂的问题，通过组合来替代继承。它主要的作用是给原始类添加增强功能。这也是判断是否该用装饰器模式的一个重要的依据。除此之外，装饰器模式还有一个特点，那就是可以对原始类嵌套使用多个装饰器。为了满足这个应用场景，在设计的时候，装饰器类需要跟原始类继承相同的抽象类或者接口。

特点：可以灵活拓展新功能，动态添加额外职责。

二、UML类图

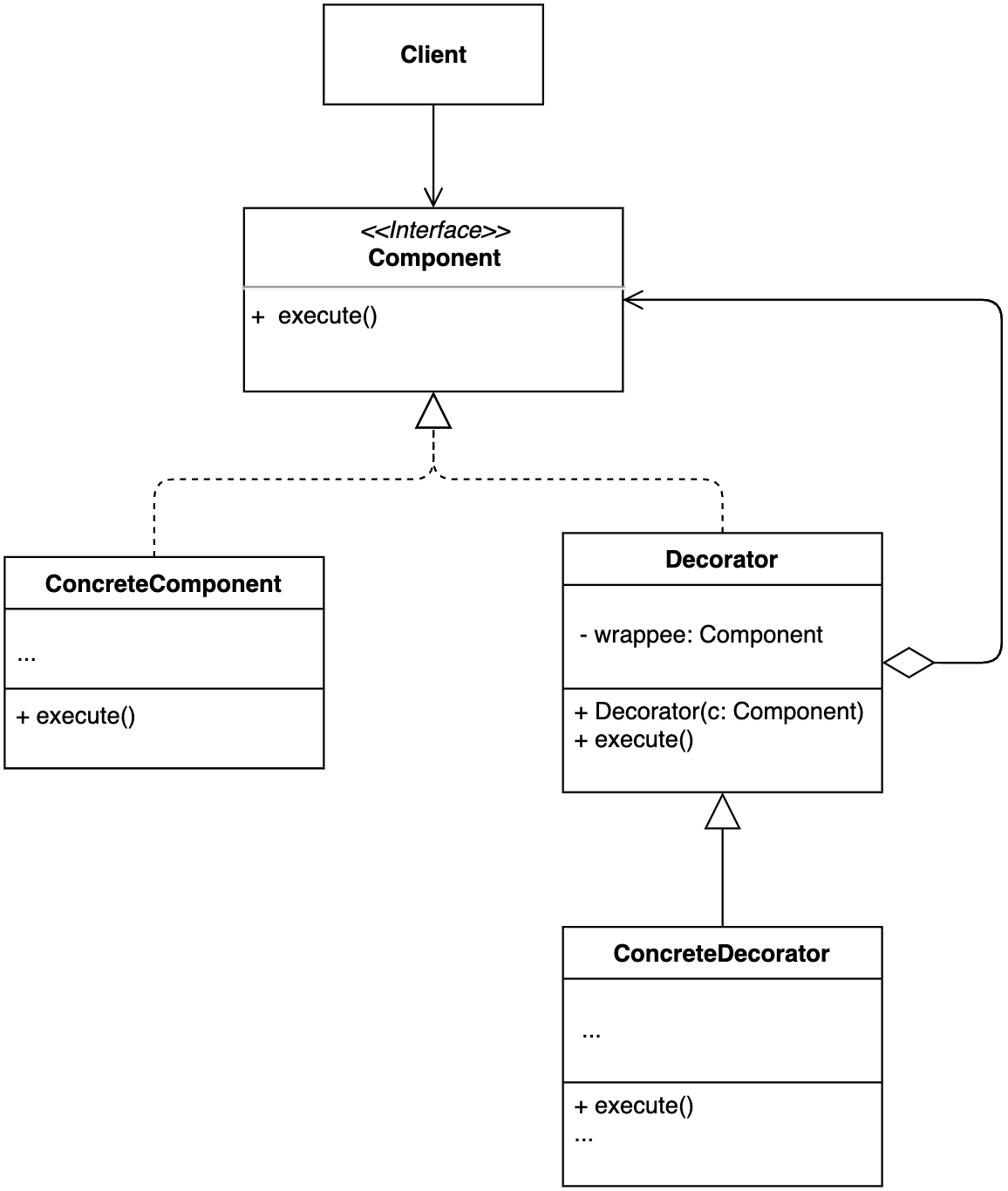
三、案例

以下案例是咖啡店里卖咖啡，可以只买咖啡，也可以加牛奶、糖等，根据选的调味料的种类来计算最终价格。

package main

import "fmt"

type Coffee interface {	
	Cost() float64
}

type SimpleCoffee struct {	
}

func (SimpleCoffee) Cost() float64 {
	return 2.0
}

type CoffeeDecorator struct {
	coffee Coffee
}

func (cd CoffeeDecorator) Cost() float64 {
	fmt.Println("ok1")
	return cd.coffee.Cost()
}

type MilkDecorator struct {
	CoffeeDecorator
}

func NewMilkDecorator(coffee Coffee) Coffee {
	md := MilkDecorator{}
	md.coffee = coffee	
	return md
}

func (md MilkDecorator) Cost() float64 {	
	return md.coffee.Cost() + 0.5
}

type SugarDecorator struct {
	CoffeeDecorator
}

func NewSugarDecorator(coffee Coffee) Coffee {
	sd := SugarDecorator{}
	sd.coffee = coffee
	return sd
}

func (sd SugarDecorator) Cost() float64 {
	return sd.coffee.Cost() + 0.25
}

func main() {
	coffee := new(SimpleCoffee)
	coffeeWithMilk := NewMilkDecorator(coffee)
	coffeeWithMilkAndSugar := NewSugarDecorator(coffeeWithMilk)
	
	fmt.Println("Coffee cost: ", coffee.Cost())
	fmt.Println("Coffee with milk cost: ", coffeeWithMilk.Cost())
	fmt.Println("Coffee with milk and sugar cost: ", coffeeWithMilkAndSugar.Cost())
}

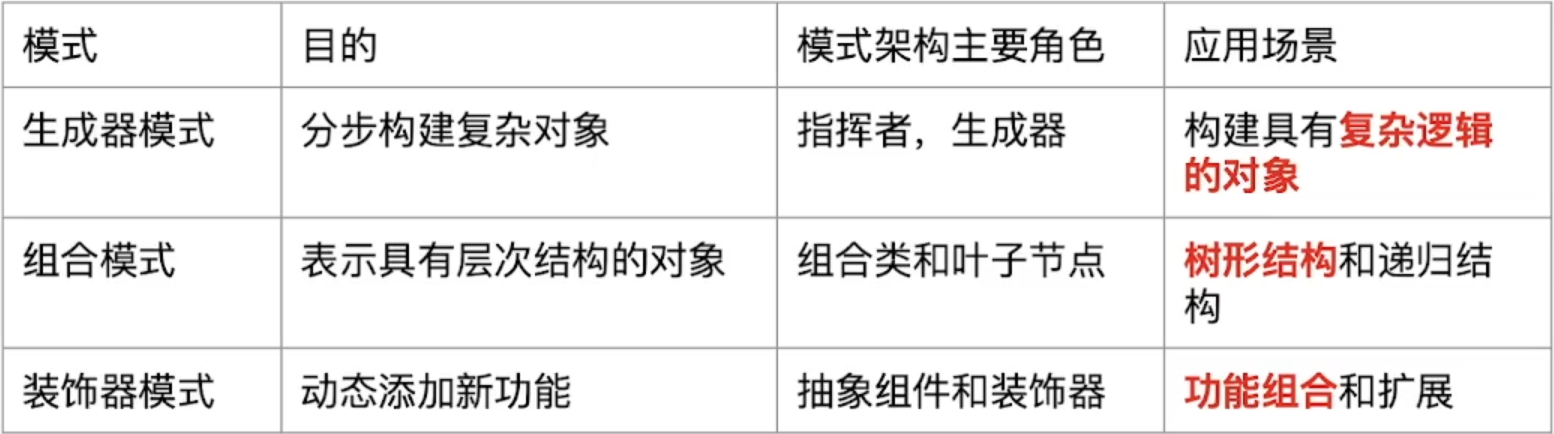
四、对比