Leetcode 43. 字符串相乘中等

news2024/9/27 9:29:02

题目 - 点击直达

1. 43. 字符串相乘中等
- 1. 题目详情
- - 1. 原题链接
  - 2. 题目要求
  - 3. 基础框架
- 2. 思路一做加法
- - 1. 思路分析
  - 2. 时间复杂度
  - 3. 代码实现
- 3. 思路二做乘法
- - 1. 思路分析
  - 2. 时间复杂度
  - 3. 代码实现

1. 43. 字符串相乘中等

1. 题目详情

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

注意：不能使用任何内置的 BigInteger 库或直接将输入转换为整数。

1. 原题链接

Leetcode 43. 字符串相乘中等

2. 题目要求

示例 1:
输入: num1 = “2”, num2 = “3”
输出: “6”

示例 2:
输入: num1 = “123”, num2 = “456”
输出: “56088”

提示：
1 <= num1.length, num2.length <= 200
num1 和 num2 只能由数字组成。
num1 和 num2 都不包含任何前导零，除了数字0本身。

3. 基础框架

● Cpp代码框架

class Solution {
public:
    string multiply(string num1, string num2) {
    }
};

2. 思路一做加法

1. 思路分析

$(1)$ 模拟两个数 $n u m 1$ 和 $n u m 2$ 相乘的过程， $n u m 1$ 的每一位数字从个位开始依次与 $n u m 2$ 的每一位数字相乘分别得到一个结果数，最后把这些结果数再相加就得到了最后的相乘结果（相加需要用到字符串相加的知识）；
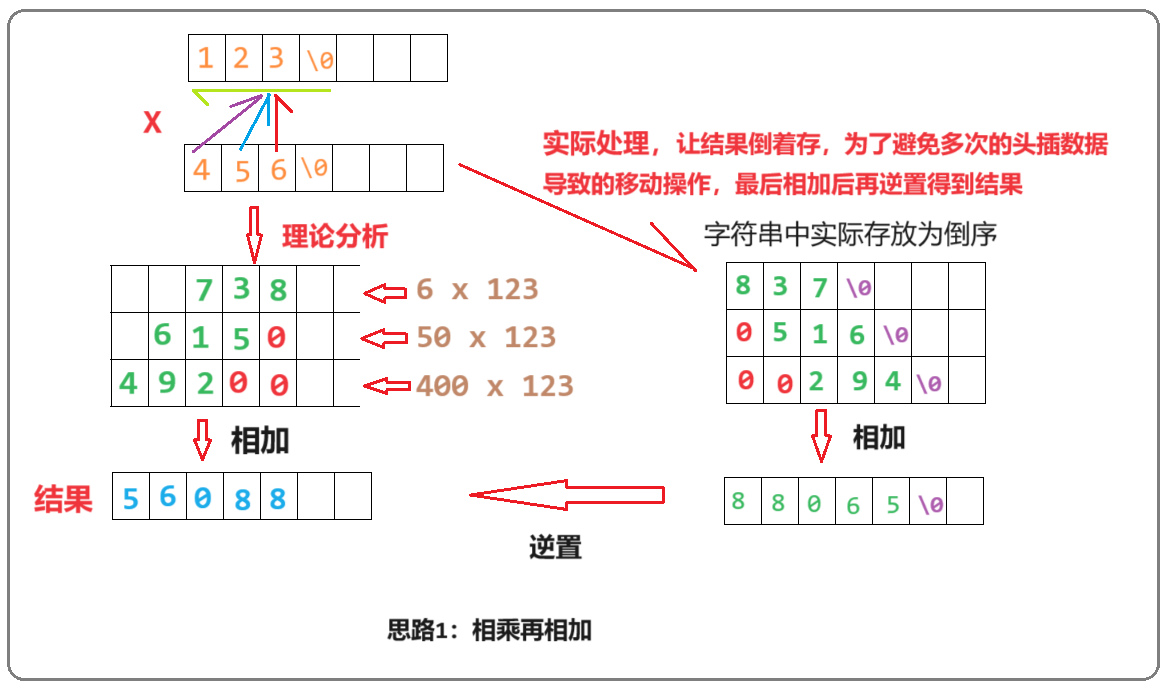
$(2)$ $n u m 1$ 的某一位与 $n u m 2$ 所有位相乘得到的结果数需要存放在字符串中，由于运算顺序是从低位到高位进行的，所以为了保证结果数在字符串中按高位到低位排列就需要一直在字符串中头插数据，而头插的效率非常低；为了提高效率，我们选择结果数按低位到高位的顺序存放，这样只需一直尾插数据，效率很高；
$(3)$ 最后所有的结果数相加得到的也是相乘结果的倒序；
$(4)$ 逆置之前去除运算产生的可能存在的无效0：
逆置之前结果是反着的，左边是低位，右边是高位

如果只有1位，且是0，是有效的0，不去除
如果有多位，低位的0和中间的0是有效的0，不去除; 高位的0(可能有多个)是无效的，需要去除
$(5)$ 逆置得到需要的相乘结果；

2. 时间复杂度

$O(mn+n^2)$
$n u m 1$ 的每一位都需要与 $n u m 2$ 的每一位相乘，共乘了 $mn$ 次；
相加的字符串长度不超过 $m + n$ ，字符串相加的操作共有n次，字符串相加的时间复杂度是 $mn + n^2$ ;
综上，时间复杂度是 $mn+n^2$

3. 代码实现

class Solution {
public:
    string multiply(string num1, string num2) {
        // 结果字符串
        string ret;
        for(int i = num1.size() - 1; i >= 0; --i){
            // num1的高位和低位与另一个数的每一位相乘的到的结果不能直接相加，高位比低位需要多乘个10才能相加;
            // 从个位开始，每高一位，就需要多乘一个10，个位相当于乘了0个10
            // 由于是从低位开始依次相乘，所以是倒着循环的，但是循环的结果是顺序存放的，最后需要逆置才是结果
            string tmp(num1.size() - i - 1, '0');
            int carry = 0;
            for(int j = num2.size() - 1; j >= 0; --j){
                int sum = (num1[i] - '0') * (num2[j] - '0') + carry;
                carry = sum / 10;
                tmp += sum % 10 + '0';
            }
            // 相乘 进位取值范围[0, 9]，与相加的进位取值范围大[0,1]
            if(carry) tmp += carry + '0';
            // += 
            add(ret, tmp);
        }
        // 逆置之前结果是反着的，左边是低位，右边是高位
        // 如果只有1位，且是0，是有效的0，不去除
        // 如果有多位，低位的0和中间的0是有效的0，不去除; 高位的0(可能有多个)是无效的，需要去除
        // 末尾0 需要去除 可能存在多个末尾0
        while(ret.size() > 1 && ret[ret.size() - 1] == '0') ret.erase(ret.size() - 1, 1);
        reverse(ret.begin(), ret.end());
        return ret;
    }
    // 大数相加，且s1和s2中存放的数是倒序的
    // 例如：存放的是 1 2 3 4 实际上对应的值是 1234
    void add(string& s1, string& s2){
        int l1 = 0;
        int l2 = 0;
        int len1 = s1.size();
        int len2 = s2.size();
        int carry = 0;
        string s;
        while(l1 < len1 || l2 < len2){
            int num1 = l1 < len1 ? s1[l1] - '0' : 0;
            int num2 = l2 < len2 ? s2[l2] - '0' : 0;
            int sum = num1 + num2 + carry;
            carry = sum / 10;
            s += sum % 10 + '0';
            l1++;
            l2++;
        }
        if(carry) s += '1';
        s1 = s;
    }
};

3. 思路二做乘法

1. 思路分析

$(1)$ 大小为 $l e n 1$ 的字符串 $n u m 1$ 和大小为 $l e n 2$ 的字符串 $n u m 2$ ，依然是数 $n u m 1$ 的每一位依次乘以 $n u m 2$ 的每一位；
与做加法思路不同的是：不是再 $^{''}$ 等到 $n u m 1$ 的这一位数与 $n u m 2$ 的所有位上的数相乘得到所有的中间结果字符串，再把所有中间结果字符串相加 $^{''}$ ，而是 $n u m 1$ 的这一位数与 $n u m 2$ 的一位数相乘后就放在最终结果字符串中的对应位置；
但是直接放在字符串中还是会涉及到字符串加法操作，为了简化操作，先用数组保存结果，等到 $n u m 1$ 和 $n u m 2$ 的所有位相乘完后再把数组中的结果复制到字符串中；
$(2)$ 依旧是从低位开始相乘，使用下标 $i$ ， $j$ 分别表示当前 $n u m 1$ 和 $n u m 2$ 进行相乘的位的下标；
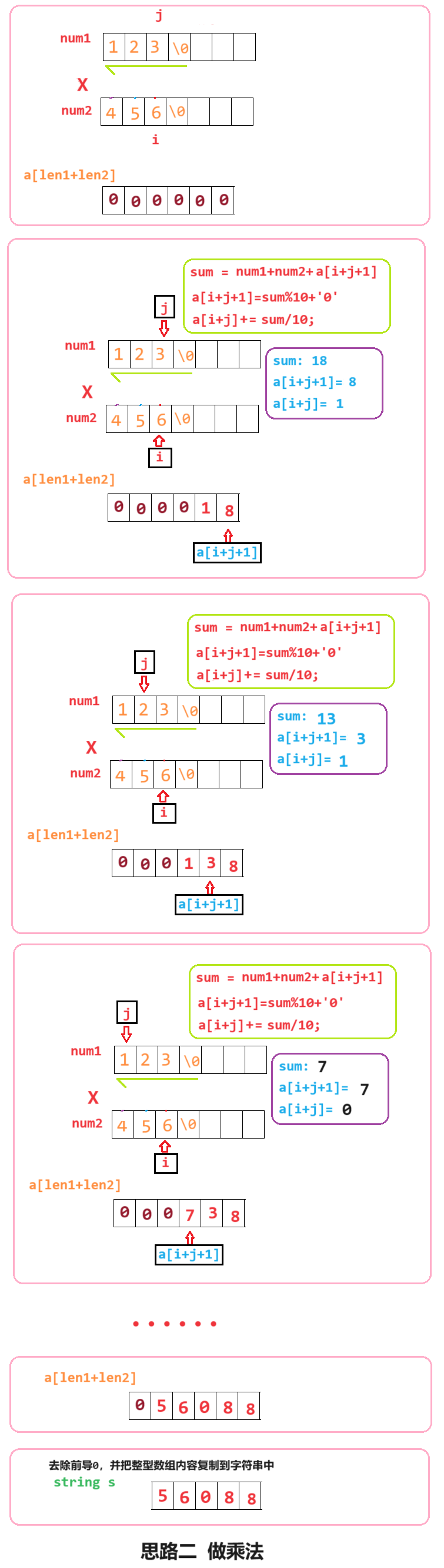
$(3)$ 计算 $n u m 1 [i] + n u m 2 [j] + a [i + j + 1]$ 的结果 $s u m$ ， $i + j + 1$ 就是 $s u m$ 将要存放的位置，如果 $s u m$ 大于等于10就除10并产生进位 $c a rry$ ，把进位 $c a rry$ 加入到 $i + j$ 位置内
$(4)$ 结果长度的范围是 $[l e n 1 + l e n 2 - 1, l e n 1 + l e n 2]$ ，如果高位存在多余的1个及以上的0时需要去除；
$(5)$ 数组中的结果复制到字符串中；
在这里插入图片描述

2. 时间复杂度

$O (nm)$
$n u m 1$ 和 $n u m 2$ 所有的位数都要相乘一次，共相乘 $nm$ 次，￥￥每一次的相加操作再整型数组中进行，是 $nm$ 次；

3. 代码实现

class Solution {
public:
    string multiply(string num1, string num2) {
        int len1 = num1.size();
        int len2 = num2.size();
        // 结果的位数范围[len1+len2-1, len1+len2];
        int a[len1 + len2];
        memset(a, 0, sizeof(int) * (len1 + len2));
        for(int i = len1 - 1; i >= 0; --i){
            for(int j = len2 - 1; j >= 0; --j){
            	// 正着存数据
                int pos = i + j + 1;
                int sum = (num1[i] - '0') * (num2[j] - '0') + a[pos];
                a[pos] = sum % 10;
                a[pos - 1] += sum / 10;
            }
        }
        //
        string ret;
        int index = 0;
        // 去除前导0，此时小坐标存放高位数据，大坐标存放低位数据
        while(len1 + len2 - index > 1 && a[index] == 0){
            index++;
        }
        // 正着取数据
        while(index < len1 + len2){
            ret += a[index] + '0';
            index++;
        }
        
        return ret;
    }
};

class Solution {
public:
    string multiply(string num1, string num2) {
        int len1 = num1.size();
        int len2 = num2.size();
        // 结果的位数范围[len1+len2-1, len1+len2];
        int a[len1 + len2];
        memset(a, 0, sizeof(int) * (len1 + len2));
        for(int i = len1 - 1; i >= 0; --i){
            for(int j = len2 - 1; j >= 0; --j){
	            // 倒着存数据
                int pos = len1 + len2 - i - j - 2;
                int sum = (num1[i] - '0') * (num2[j] - '0') + a[pos];
                a[pos] = sum % 10;
                a[pos + 1] += sum /10;
            }
        }
        //
        string ret;
        int index = len1 + len2 - 1;
        // 去除无效的0，此时小坐标存放低位数据，大坐标存放高位数据
        while(index > 0 && a[index] == 0){
            index--;
        }
        // 倒着取数据
        for(int i = index; i >= 0; --i){
            ret += a[i] + '0';
        }
        //
        return ret;
    }
};