题目

        给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环。

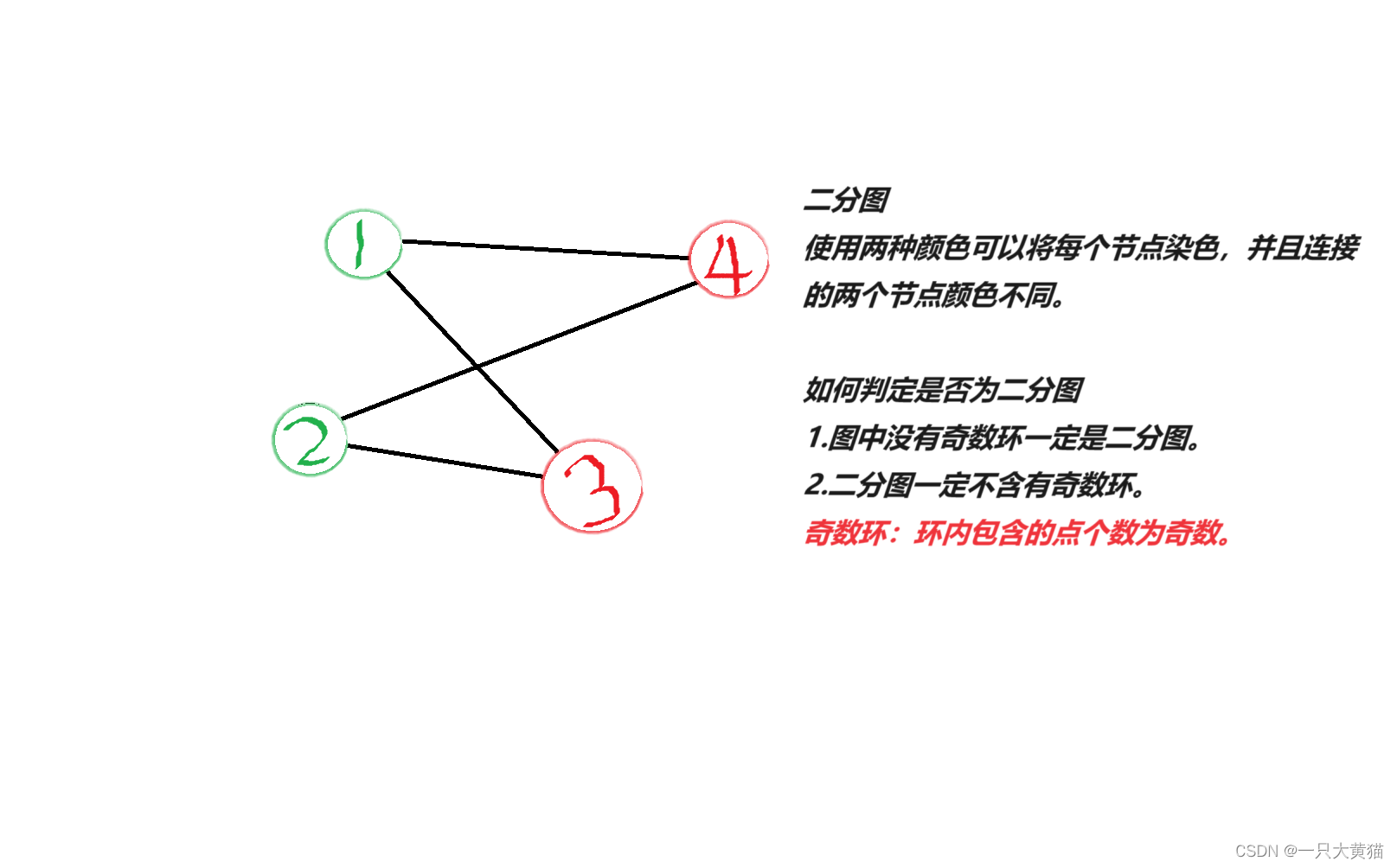
        请你判断这个图是否是二分图。

输入格式

        第一行包含两个整数 n 和 m。

        接下来 m 行，每行包含两个整数 u 和 v，表示点 u 和点 v 之间存在一条边。

输出格式

        如果给定图是二分图，则输出 Yes，否则输出 No。

数据范围

        1 ≤ n , m ≤ 10^5。

思路

        一个图如果不存在奇数环，则肯定是二分图。一个图是二分图，则肯定不存在奇数环。

         使用深搜（其实宽搜也可以），首先使用邻接表四件套建立无向图，依次从1~n点进行深搜染色，如果相邻两个点颜色后颜色相同，则说明存在奇数环，返回false。如果所有点都染色成功，并且相邻点的颜色均不相同，则表明该图没有奇数环，是一个二分图，返回true。

代码 

#include<bits/stdc++.h>
#define int long long
#define N 100010 // 点数的最大值
#define M 200010 // 建立无向边的边数
using namespace std;

int n,m;// 点数边数
int h[N],e[M],ne[M],idx; // 邻接表四件套
int color[N]; // 储存点i的颜色
void add(int a,int b) // 添加边
{
    e[idx] = b,ne[idx] = h[a],h[a] = idx ++;
}

bool dfs(int u,int c)// u表示点，c表示颜色
{
    color[u] = c; // 将点u染为颜色c
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(!color[j])// 如果该点没有颜色，则进行dfs对其进行染色
        {
            if(!dfs(j,3-c)) return false;// 颜色分为1，2
        }
        else if(color[j] == c) return false;// 如果该点有颜色，判断该点的颜色与u的颜色是否相同，如果相同则代表有奇数环
    }
    return true;
}
int32_t main()
{
    cin >> n >> m;
    memset(h,-1,sizeof(h));// 将头节点初始化为-1
    while(m --)
    {
        int a,b;
        cin >> a >> b;
        add(a,b);
        add(b,a);
    }
    bool flag = true;
    for(int i = 1;i <= n; i ++)// 防止存在没有遍历的点存在（防止该图不是连通图）
    {
        if(!color[i])// 如果当前点没有染色，则进行染色
        {
            if(!dfs(i,1))// 如果当前点染色失败（存在奇数环），则返回false，并结束循环
            {
                flag = false;
                break;
            }
        }
    }
    if(flag) cout << "Yes" << endl;
    else
        cout << "No" << endl;
    return 0;
}