文章目录
- 📑前言
- 🌤️归并排序的思想
- ☁️基本思想
- ☁️归并的思想实现
- ☁️分治法
- 🌤️归并排序的实现
- ☁️核心操作步骤
- ☁️递归版归并实现
- ⭐代码实现详解:
- ☁️非递归版归并实现
- ⭐代码实现详解:
- 🌤️归并排序特性总结
- 🌤️全篇总结
📑前言
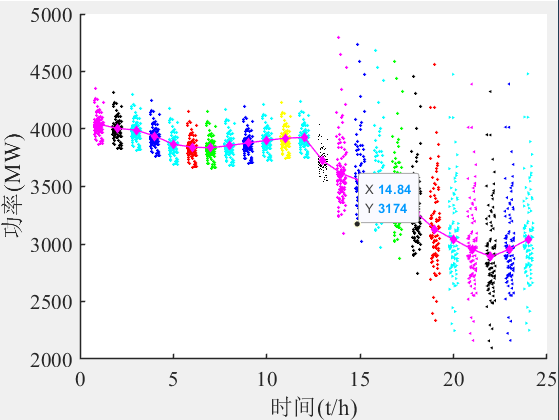
什么是归并?通过归并排序就能让数据有序?分治法是怎么在归并排序上应用的?本文将对归并排序进行细致入微的讲解,庖丁解牛般让你彻底明白归并排序!
🌤️归并排序的思想
☁️基本思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。
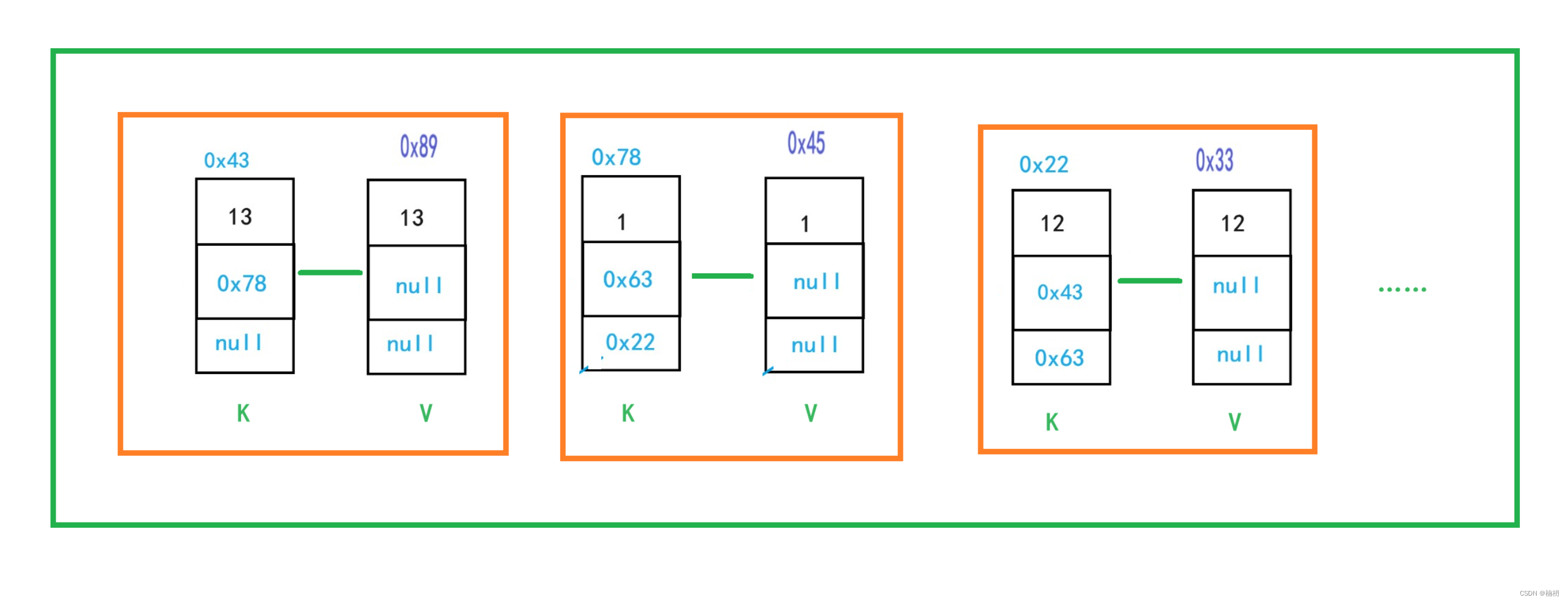
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
☁️归并的思想实现
将两个有序数组合并成一个有序数组的操作。在归并排序中,通过不断地将数组分成两半,分别对每一半进行排序,然后将排好序的两个子数组合并成一个有序数组,最终得到整个数组有序的结果。
☁️分治法
分治法在归并排序中的应用是将问题分解成更小的子问题,然后分别解决这些子问题,最后将子问题的解合并起来得到原问题的解。具体来说,归并排序的分治法应用如下:
- 分解:将待排序的数组分成两个子数组,分别为左子数组和右子数组。
- 解决:递归地对左子数组和右子数组进行归并排序。
- 合并:将排好序的左子数组和右子数组合并成一个有序数组。
🌤️归并排序的实现
☁️核心操作步骤
静图全步骤概览:

动图一步步的逻辑实现:

☁️递归版归并实现
//归并
void _MergeSort(int* a, int* tmp, int begin, int end)
{
if (end <= begin)
{
return;
}
int mid = (begin + end) / 2;
_MergeSort(a, tmp, begin, mid);
_MergeSort(a, tmp, mid + 1, end);
// a->[begin, mid][mid+1, end]->tmp
//归并
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int index = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
//归并(递归版)
void MergeSort(int* a, int n)
{
int* tmp = malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
_MergeSort(a, tmp, 0, n - 1);
free(tmp);
}
归并需要开一个同样大的tmp数组来存放数据,相当于是拿空间来换时间了.
⭐代码实现详解:
- 首先,将整个序列分为两部分,分别递归调用_MergeSort函数对左右两部分进行排序。
- 在_MergeSort函数中,首先判断递归终止条件,如果end小于等于begin,则表示当前子序列只有一个元素或者为空,无需排序,直接返回。
- 然后,计算中间位置mid,并分别递归调用_MergeSort函数对左右两部分进行排序。
- 接下来,进行归并操作。首先,设置四个指针begin1、end1、begin2、end2分别指向左右两部分的起始和结束位置,以及一个指针index指向当前归并结果的位置。
- 然后,使用两个循环比较左右两部分的元素大小,并将较小的元素放入tmp数组中,同时移动相应的指针。
- 最后,将剩余的元素复制到tmp数组中。
- 最后,将tmp数组中的元素复制回原数组a中,完成归并排序。
☁️非递归版归并实现
非递归版是在递归上进行了修改,将其递归改为了循环。
//归并(非递归版)
void _MergeSortNotR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
if (begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
memcpy(a+i, tmp+i, (end2-i+1) * sizeof(int));
}
gap *= 2;
}
free(tmp);
}
⭐代码实现详解:
-
分配一个临时数组tmp,用于存储归并结果。
-
设置一个变量gap为1,表示归并的间隔大小。
-
接下来,循环执行以下操作,直到gap大于等于n:
-
- 遍历整个数组,每次取两个相邻的子序列进行归并。
- 计算左右两个子序列的起始和结束位置。
- 判断右子序列的结束位置是否超过了数组的长度,如果超过,则将结束位置设置为数组的最后一个元素的下标。
- 使用两个指针begin1和begin2分别指向左右两个子序列的起始位置,使用指针end1和end2分别指向左右两个子序列的结束位置。
- 使用一个指针index指向当前归并结果的位置。
- 使用一个循环,比较左右两个子序列的元素大小,并将较小的元素放入临时数组tmp中,同时移动相应的指针。
- 如果左子序列还有剩余元素,则将剩余元素复制到tmp数组中。
- 如果右子序列还有剩余元素,则将剩余元素复制到tmp数组中。
- 将tmp数组中的元素复制回原数组a中。
- 将gap乘以2,进行下一轮归并。
-
最后,释放临时数组tmp的内存空间。
🌤️归并排序特性总结
- 稳定性:归并排序是一种稳定的排序算法,即相等元素的相对顺序在排序后不会改变。
- 时间复杂度:归并排序的时间复杂度是O(nlogn),其中n是待排序序列的长度。这是由于归并排序的核心操作是将序列分成两个子序列,然后分别进行排序,再将排序好的子序列合并,而分割和合并操作都需要O(logn)的时间,所以总的时间复杂度是O(nlogn)。
- 空间复杂度:归并排序的空间复杂度是O(n),其中n是待排序序列的长度。这是由于归并排序需要一个与待排序序列相同大小的额外空间来存储临时的合并结果。
- 非原地排序:归并排序不是原地排序算法,即它需要额外的空间来存储临时的合并结果。这是因为在合并操作中,需要同时访问两个子序列的元素,并将它们按照顺序合并到一个新的序列中。
- 递归实现:归并排序通常使用递归的方式来实现,即将待排序序列不断分割成更小的子序列,直到子序列的长度为1,然后再将这些子序列按照顺序合并成一个有序的序列。递归实现的归并排序代码简洁易懂,但是由于递归调用的开销比较大,所以在实际应用中可能会使用迭代的方式来实现归并排序。
- 适用性:归并排序适用于各种数据规模的排序,而且对于大规模数据的排序效果较好。它的时间复杂度稳定在O(nlogn),不会因为数据规模的增大而导致时间复杂度的增加。此外,归并排序还适用于外部排序,即对于无法一次性加载到内存的大规模数据进行排序。
🌤️全篇总结
经过对归并排序的思想,特性,代码实现这些细致入微的讲解,相信聪明的你肯定已经学会了叭😊😊!
☁️ 好了,由于篇幅有限,本章只是对归并进行了深度解刨,后序会出更多的排序算法哦!
看到这里了希望给博主留个:
👍 点赞🌟收藏 ⭐️ 关注!
💛 💙 💜 ❤️ 💚💓 💗 💕 💞 💘 💖
拜托拜托这个真的很重要!
你们的点赞就是博主更新最大的动力!
有问题可以评论或者私信呢秒回哦。