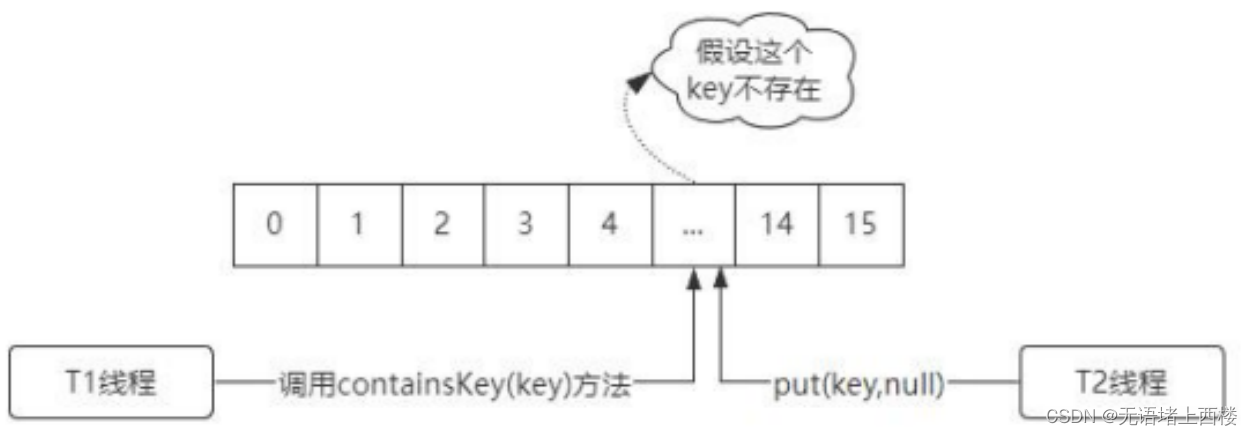
定点数:
原码的乘法:

乘法的符号位是单独处理的(通过对被乘数和乘数的符号位进行异或实现),数值位去绝对值进行运算。这里的乘法实际上是通过多次加法实现的。
这里被乘数是放在x寄存器,乘数放在MQ寄存器里,乘法运算的实现是第一次乘数的最低一位乘以被乘数然后放在ACC里,然后ACC和MQ里面的数据都右移,ACC空出的高位补零,MQ空出的高位由ACC移出的低位补上,MQ移出的低位舍弃(所以说ACC中存放的是乘积高位,MQ中存放的乘数和乘积的低位),然后这样MQ中的最低位就变成了要参加乘法的下一位,在再次运算之后(除第一次外)运算结果和ACC里存放的值相加然后再放入ACC中(注意刚才ACC移位的目的)。这样通过先加法再移位的反复操作,直到MQ的最后一位是乘数的符号位则结束运算(乘数的符号位不用参与运算),这里最后还要对乘积的符号位进行修改。
这里还有个手算模拟,应该是会考,可以先看看。

补码乘法运算:Booth算法
补码一位乘法:进行n轮加法,移位,最后要再多一次加法;(多的这一次就是符号位的运算)
每次加法加的可能是 0 ,x的补码 ,(-x)的补码。
而且相比于原码移位是逻辑移位(补0),补码的移位是算数移位,而且符号位参与运算。
补码的算术右移符号位是不动的,数值位右移,高位补的和符号位一致。
至于究竟加什么,由MQ中的最低位和辅助位来确定。
辅助位 - MQ最低位 = 1时,加x的补码; = 0 时 加 0 ;= -1时加(-x)的补码。

对于补码的话,加法器的各个寄存器就多了一位,MQ中的用来当辅助位,而ACC和X中的被用来当双符号位。辅助位的值是会改变的,除了初始为0,后面由右移从乘数移出的低位代替。
除法运算:
恢复余数法:

原码的除法的符号位也是单独处理,通过异或实现,数值位取绝对值进行运算,乘法是ACC加上运算结果,除法是ACC减去运算结果。
在运算的时候计算机会在MQ的最低位先商 1 ,如果这个时候被除数(余数,第一次被除数,后面的都是余数)与除数相减之后得到的值小于 0 (符号位为1),就会改商值为 0 ,然后 恢复余数 (把现在这个相减之后小于 0 的余数在加上除数,得到的就是之前的那个余数),注意这个虽然是原码的除法,但在减去除数的时候,用的是 (-|y|)的补码,在恢复余数的时候加的是 |y|的补码。
之后的每一次都是ACC,MQ整体“逻辑左移”,ACC的高位丢弃,MQ低位补0,然后MQ的最低位商1/0,得到余数,余数末位补0,这里要注意的是如果最后一步商的余数为 负 ,也是需要恢复余数,并改商为 0 的 。这里ACC在每一次运算之后存储的余数的最高位好像一定是 0 ,所以不会出现精度丢失的问题,要是丢了也不能叫精度丢失了,重大事故了就,不过没有具体验证。
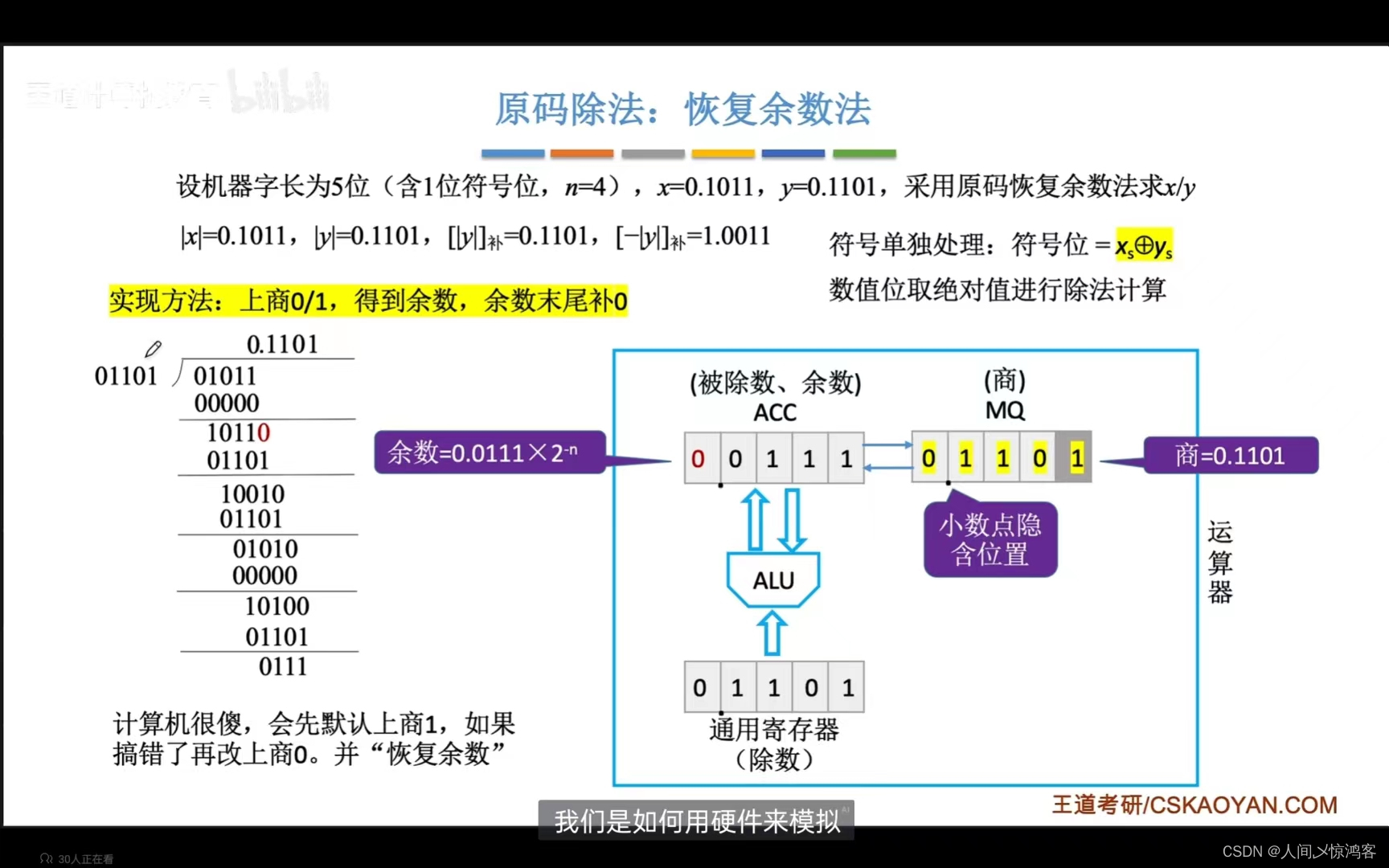
然后这里也有原码除法的恢复余数法的手算,可以尝试一下。
原码除法:
加减交替法/不恢复余数法:

上面这张图是下面这种图为什么可以这样处理的原因。这里其实也蛮巧妙的额,不过更像是由数据得出的结果,而非逻辑的推理。

加减交替法和恢复余数法的区别在于,回复余数法是先商值然后再确定余数的,根据余数的值再反过来确定商值是否正确,而恢复余数法则是先计算余数,根据余数的正负来判断商0/1,然后根据余数的正负对余数进行处理得到下一个新余数,然后再根据这个新余数的值确定下一位商值,这样重复直至得出结果,这里如果最后的出的余数为负,则再商0之后,还需要对余数再处理一下(加 |y| 的补码,就是恢复余数的那个东西)得到正确的余数。
补码除法: 加减交替法
补码的除法和乘法符号位都参与运算,且被除数/余数和除数都采用双符号位。
补码的乘法的右移是算数右移,而补码的除法的左移是逻辑左移,不过好像补码的逻辑左移和算数左移是一样的,都是低位补 0 .
补码除法的运算规则是:
被除数和除数同号的时候,被除数减去除数,异号则加上除数,注意这里还没有开始商,商值是从第一个余数开始的
余数和除数同号时,商 1 ,余数左移一位减去除数;异号时,商 0 ,余数左移一位 加上除数。重复数值位位数。
补码除法的商值末位商恒置为 1 。

这道题怎么说呢,好像也不难,但让我感觉不舒服。下面的两种都是我写的,一个很长,一个很短...

int main()
{
int n = 0;
scanf("%d", &n);
int i = 0;
for (i = 2; ; i++)
{
if (n % i == 0)
{
printf("%d", n / i);
break;
}
}
return 0;
}int main()
{
int n = 0;
scanf("%d", &n);
int i = 0;
int max = 0;
for (i = 1; i <= sqrt(n); i++)
{
if (n % i == 0)
{
int j = 0;
int flag = 1;
for (j = 2; j <= sqrt(i); j++)
{
if (i % j == 0)
{
flag = 0;
break;
}
}
if (flag)
{
int m = n / i;
for (j = 2; j <= sqrt(m); j++)
{
if (m % j == 0)
{
flag = 0;
break;
}
}
if (flag)
{
int a = m > i ? m : i;
max = max > a ? max : a;
}
}
}
}
printf("%d", max);
return 0;
}