原来的解释来自维基百科：https://en.wikipedia.org/wiki/Resistance_distance

在图论中，简单连通图G的两个顶点之间的电阻距离等于电网上两个等效点之间的电阻，电网被构造为与G相对应，每条边被一欧姆的电阻代替。它是图上的度量。

1.定义：

在图G上，两个顶点和vj之间的电阻距离Ωi，j为:

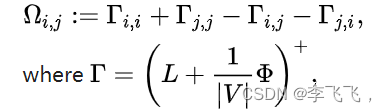
其中+表示Moore–Penrose逆， L是G的拉普拉斯矩阵，|V|是G中的顶点数，Φ 是|V| × |V| 的全 1 的矩阵。

2.电阻距离特性

3.一般求和规则

对于任意N顶点的简单连通图G=（V，E）和任意N×N矩阵M：

根据这个广义和规则，可以根据M的选择导出许多关系。 值得注意的两个是：

 

其中 是拉普拉斯矩阵的非零特征值。这个无序的总和 

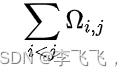
称为图的Kirchhoff index。 

4.与图的生成树数的关系

对于简单连通图G=（V，E），两个顶点之间的电阻距离可以表示为G的生成树集合T的函数，如下所示：

翻译这段话就是：

其中T’是图G’=（V，E+E，）的生成树的集合。换句话说，对于边（i，j）∈E，一对节点i和j之间的电阻距离是边 (i,j) 位于G的随机生成树中的概率。

5.与随机游走的关系

翻译就是：顶点u和u之间的阻力距离与u和v之间随机行走的通勤时间Cu成比例。通勤时间是从u开始、访问v并返回u的随机行走的预期步数。对于具有m条边的图，阻力距离和通勤时间相关为C'u，=2mDu，.l

6.作为欧几里得距离的平方

由于拉普拉斯算子L是对称的和半正定的，因此

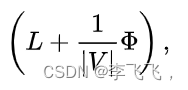
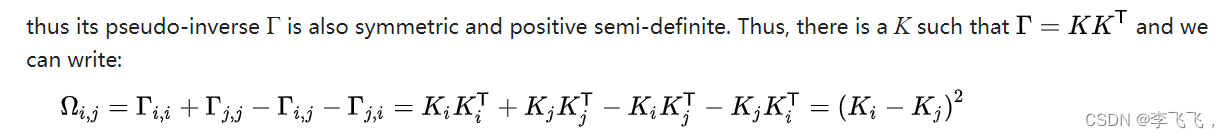
表明电阻距离的平方根对应于 K 所跨越的空间中的欧几里得距离。 

7.与斐波那契数的联系