分治法求解棋盘覆盖问题

如何应用分治法求解棋盘覆盖问题呢？分治的技巧在于如何划分棋盘，使划分后的子棋盘的大小相同，并且每个子棋盘均包含一个特殊方格，从而将原问题分解为规模较小的棋盘覆盖问题。

基本思路

棋盘覆盖问题是指在一个大小为2n * 2n的棋盘上，去掉其中一个方格后，用L型骨牌（覆盖3个方格）将其完全覆盖。分治法是一种解决该问题的有效算法。

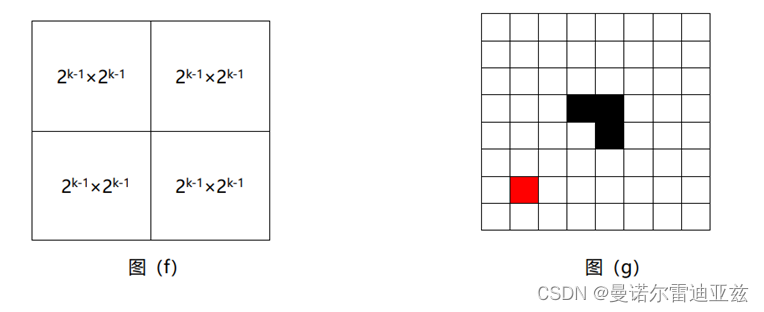
当 k>0 时，将 2^k * 2^k 棋盘分割为 4 个 2^(k-1) * 2^(k - 1)子棋盘，如下图(f)所示。特殊方格必位于4 个较小子棋盘之一种，其余 3 个子棋盘中无特殊方格。为了将这 3 个无特殊方格的子棋盘转化为特殊棋盘，可以用一个 L 型骨牌覆盖这 3 个较小棋盘的会合处，如下图(g)所示。从而将原问题转化为 4 个较小规模的棋盘覆盖问题。递归地使用这种分割，直至棋盘简化为棋盘 1*1。

代码实现

#include <stdio.h>
int board[100][100] = { 0 };
int tile = 1;
//棋盘覆盖 
void ChessBoard(int tr, int tc, int dr, int dc, int size) {
	if (size == 1)
		return;
	int t = ++tile,
		s = size / 2;
	//覆盖左上角棋盘
	if (dr < tr + s && dc < tc + s)
		//特殊方格在棋盘中
	{
		ChessBoard(tr, tc, dr, dc, s);
	}
	else {
		//特殊方格不在棋盘中，则从中间覆盖一个方格
		board[tr + s - 1][tc + s - 1] = t; //赋值特殊方格类型
		ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s);//从左上角继续划分 
	}
	//覆盖右上角棋盘
	if (dr < tr + s && dc >= tc + s)
		//特殊方格在棋盘中
	{
		ChessBoard(tr, tc + s, dr, dc, s);
	}
	else {
		//特殊方格不在棋盘中，则从中间覆盖一个方格
		board[tr + s - 1][tc + s] = t; //赋值特殊方格类型
		ChessBoard(tr, tc + s, tr + s - 1, tc + s, s);//从右上角继续划分 
	}
	//覆盖左下角棋盘
	if (dr >= tr + s && dc < tc + s)
		//特殊方格在棋盘中
	{
		ChessBoard(tr + s, tc, dr, dc, s);
	}
	else {
		//特殊方格不在棋盘中，则从中间覆盖一个方格
		board[tr + s][tc + s - 1] = t; //赋值特殊方格类型
		ChessBoard(tr + s, tc, tr + s, tc + s - 1, s);//从左下角继续划分 
	}
	//覆盖右下角棋盘
	if (dr >= tr + s && dc >= tc + s)
		//特殊方格在棋盘中
	{
		ChessBoard(tr + s, tc + s, dr, dc, s);
	}
	else {
		//特殊方格不在棋盘中，则从中间覆盖一个方格
		board[tr + s][tc + s] = t; //赋值特殊方格类型
		ChessBoard(tr + s, tc + s, tr + s, tc + s, s);//从左下角继续划分 
	}
}
int  main(void) {
	int size, dr, dc;
	printf("请输入棋盘的行或列号:");
	scanf("%d", &size);
	printf("请输入特殊方格的行或列号:");
	scanf("%d %d", &dr, &dc);
	board[dr][dc] = 1;
	ChessBoard(0, 0, dr, dc, size);
	for (int i = 0;i < size;i++) {
		for (int j = 0;j < size;j++)
			printf("%d\t", board[i][j]);
		printf("\n");
	}
	return 0;
}

运行结果

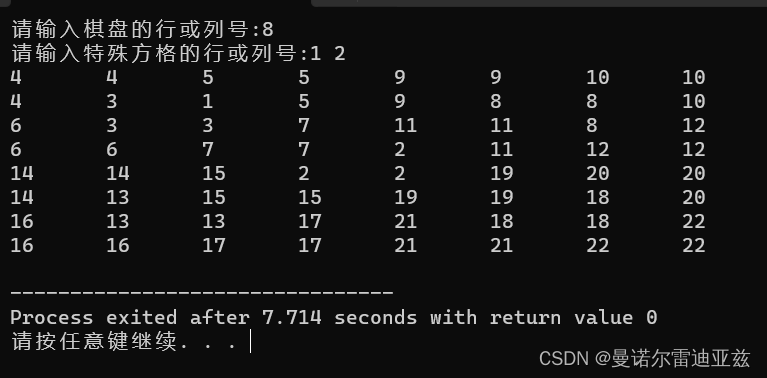
如上图所示，相同的数字就代表了一个L型的骨牌。