目录
一、前言
二、时间复杂度
1.时间复杂度定义
2.时间复杂度描述方法
三、实例代码
实例1(取影响最大的项)
实例2(舍去系数)
实例3(不确定大小关系的用max函数取最大)
实例4(常数次的时间复杂度取O(1))
实例5(取最坏时间复杂度)
实例6(不能通过循环层次确定时间复杂度,需要理解算法思想)
实例7(时间复杂度中,以2为底的对数可以省略底数2,直接写成logN,但是其他底数不可以省略)
实例8(递归的时间复杂度是递归的次数)
实例9(双目递归的时间复杂度)
一、前言
如何衡量一个算法的好坏?
看时间复杂度和空间复杂度
二、时间复杂度
1.时间复杂度定义
在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。
一个算法所花费的时间与其中语句执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
2.时间复杂度描述方法
大O复杂度表示法
求算法中语句的执行次数总和:
(1)取影响最大的项
(2)舍去系数
(3)常数次的时间复杂度取O(1)
(4)不确定大小关系的,用max函数取最大
(5)求和出现多种情况的,取最坏时间复杂度
(6)不可根据循环层次来确定时间复杂度,需要明白算法思想确定时间复杂度
(7)时间复杂度中,以2为底的对数可以省略底数2,直接写成logN,但是其他底数不可以省略
(8)递归的时间复杂度是递归的次数
三、实例代码
实例1(取影响最大的项)
F(N)=N*N+2N+10
时间复杂度:O(N^2)
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N; ++i)
for (int j = 0; j < N; ++j)
++count;
for (int k = 0; k < 2 * N; ++k)
++count;
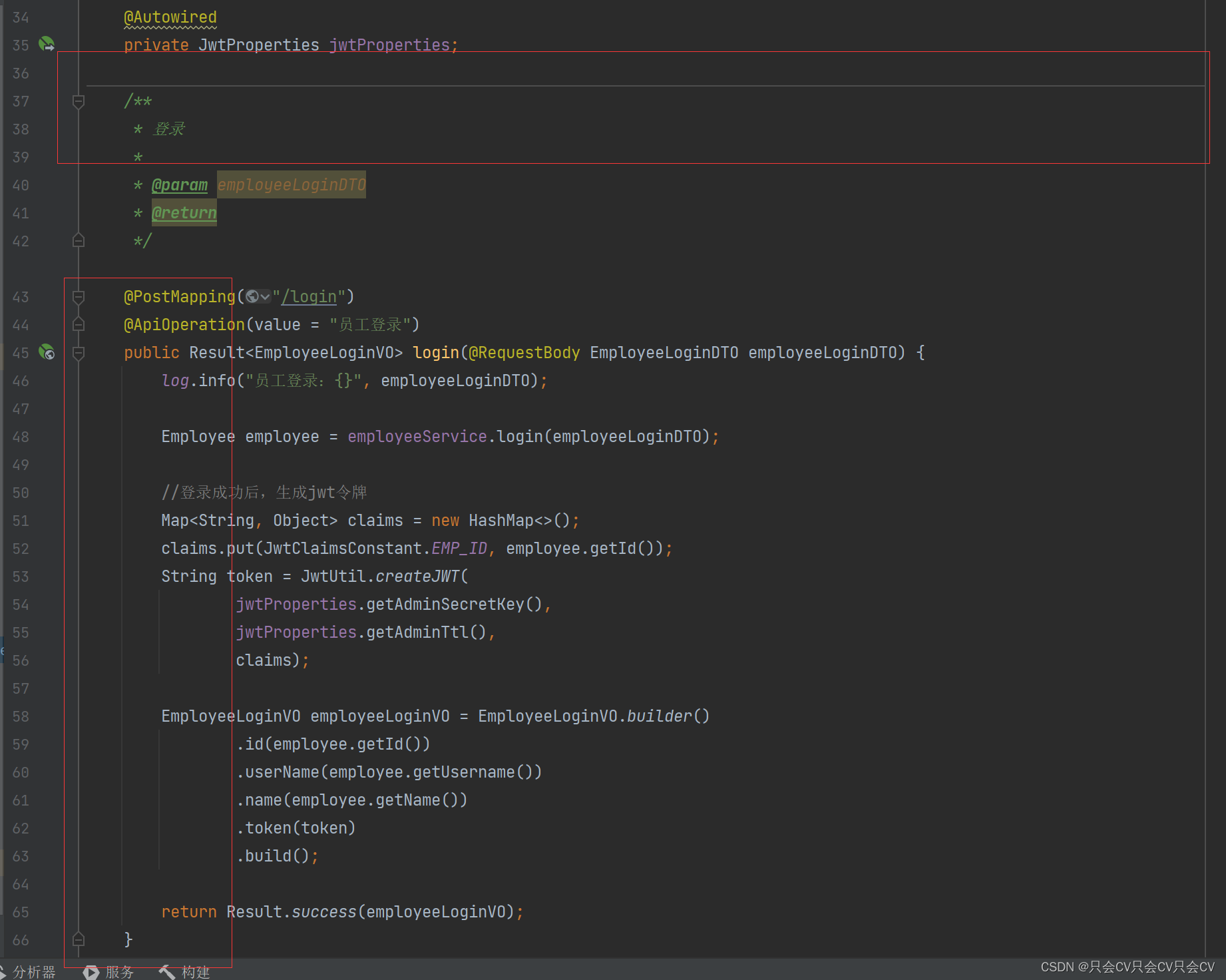
int M = 10;
while (M--)
++count;
}实例2(舍去系数)
F(N)=2N+10
时间复杂度:O(N)
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N; ++k)
++count;
int M = 10;
while (M--)
++count;
}实例3(不确定大小关系的用max函数取最大)
F(N)=M+N
时间复杂度:O(max(M,N))
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++k)
++count;
for (int k = 0; k < N; ++k)
++count;
}实例4(常数次的时间复杂度取O(1))
(常数次的时间复杂度取O(1), O(1)并不是代表1次,而是常数次)
F(N)=200
时间复杂度:O(1)
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 200; ++k)
++count;
}实例5(取最坏时间复杂度)

时间复杂度:O(N)
const char* strchr(const char* str, int character)
{
while (*str)
{
if (*str == character)
return str;
++str;
}
}实例6(不能通过循环层次确定时间复杂度,需要理解算法思想)
这是一个快速排序(Quick Sort)算法的核心代码,函数Swap用来交换两个变量的值,函数PartSort用来进行快排的分区操作
具体地,快速排序的思想是通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个过程可以递归进行。
在PartSort函数中,首先选取最左边的元素作为关键字keyi,使用两个指针left和right分别从数组的左端和右端开始向中间扫描,找到第一个大于等于关键字的元素和第一个小于等于关键字的元素,然后交换它们的位置,直到left和right相遇。最后再将关键字元素与left所指向的元素进行交换,此时,keyi左边的元素均小于等于keyi,右边的元素均大于等于keyi,完成了一次分区操作。
时间复杂度:O(N)
int PartSort(int* a, int left, int right)
{
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])//找小
--right;
while (left < right && a[left] <= a[keyi])//找大
++left;
Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);
}实例7(时间复杂度中,以2为底的对数可以省略底数2,直接写成logN,但是其他底数不可以省略)
时间复杂度:O(logN)

//整型有序数组的二分查找法
int binary_search(int arr[], int size, int num)
{
int left = 0;
int right = size - 1;
int mid = (right - left) / 2 + left;//优化取平均值的计算方法
while (left <= right)
{
if (arr[mid] < num)
{
left = mid + 1;
mid = (right - left) / 2 + left;
}
else if (arr[mid] > num)
{
right = mid - 1;
mid = (right - left) / 2 + left;
}
else if (arr[mid] == num)
{
return mid;
}
}
return -1;
}实例8(递归的时间复杂度是递归的次数)
时间复杂度:O(N)
//求n的阶乘
long long Fac(long long n)
{
assert(n >= 1);
if (n == 1)
return 1;
else
return n * Fac(n - 1);
}实例9(双目递归的时间复杂度)

其实这样计算一种粗略的计算,因为上图二叉树实际上是不满的。但由于时间复杂度的计算本身就是估算,所以不影响。
F(N)=2^0+2^1+2^2+……+2^(N-3)+2^(N-2) = 2^(N-1)+2^0
时间复杂度:O(2^N)
该算法效率极其低,实用性不大,且2^n结果随着n的增大是指数性暴增
//求斐波那契数列前n项和
long long Fibonaci(long long n)
{
if (n < 3)
return 1;
else
return Fibonaci(n - 1) + Fibonaci(n - 2);
}