一、值函数

        几乎所有的强化学习算法都涉及到估计值函数——状态（或状态-动作对）的函数，这些函数估计代理处于给定状态（或在给定状态下执行给定动作）的好坏。这里的“好坏”概念是根据可以预期的未来奖励来定义的，或者更准确地说，是根据预期回报来定义的。当然，代理未来能期望获得的奖励取决于它将采取的行动。因此，值函数是根据特定的策略来定义的。

        回顾一下，策略π是一个从每个状态s∈S和一个动作a∈(s)映射到采取动作a时处于状态s的概率π(a|s)。一般来讲，在策略π下状态s的值，记作vπ(s)，是在s开始并遵循π以后的预期回报。对于MDP（马尔可夫决策过程），我们可以正式定义vπ(s)。

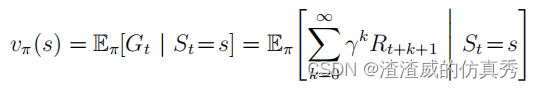
        其中，Eπ[·]表示在代理遵循策略π的情况下，某个随机变量的预期值，t是任意时间步。请注意，终端状态的值（如果有的话）始终为零。我们将函数vπ称为策略π的状态值函数。

        同样，我们定义了在状态下执行动作a的值的策略π，表示为qπ(s, a)，作为从s开始，执行动作a，之后遵循策略π的预期回报。

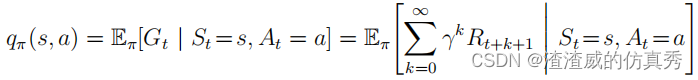
我们将qπ称为策略π的动作值函数。

二、经验积累的作用

        值函数vπ和qπ可以从经验中进行估计。例如，如果代理遵循策略π并保持每个状态的实际回报的平均值，那么当遇到该状态次数足够多时，平均值将收敛于状态的值vπ(s)。如果对于每个状态采取的动作保持单独的平均值，那么这些平均值将同样收敛于动作值qπ(s, a)。我们称这种估计方法为蒙特卡罗方法，因为它们涉及对实际回报的许多随机样本进行平均。第5章将介绍这些方法。当然，如果状态非常多，那么对每个状态单独保持平均值可能不切实际。相反，代理必须将vπ和qπ作为参数化函数进行维护，并调整参数以更好地匹配观察到的回报。这也可以产生准确的估计，尽管这在很大程度上取决于参数化函数近似器的性质。强化学习和动态规划中使用的值函数的基本属性是它们满足特定的递归关系。对于任何策略π和任何状态s，以下一致性条件在s的值与其可能的后继状态的值之间成立。

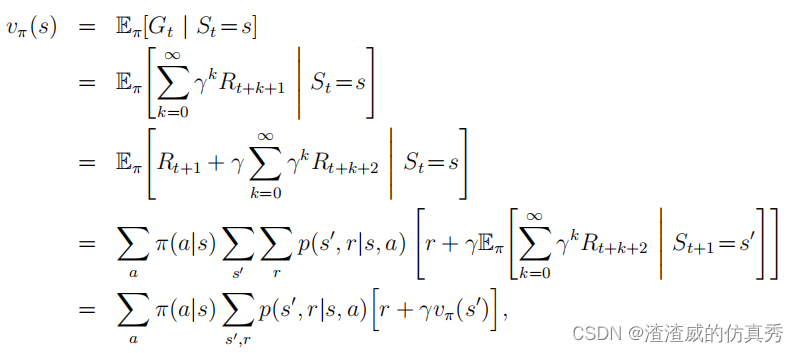
        其中隐含了从集合A(s)中采取的动作a，从集合S（在离散问题的情况下，从S+）中选取的下一个状态s0，以及从集合R中获得的回报r。请注意，在最后一个方程中，我们将两个求和合并成一个，一个是对所有s0值的求和，另一个是对所有r值的求和，合并成对所有可能值的求和。我们将经常使用这种合并求和的方法来简化公式。请注意，最终表达式可以很容易地作为期望值来解读。它实际上是对三个变量a、s0和r的所有可能值的概率的加权平均值之和。对于每个三重奏，我们计算其概率π(a|s)p(s0, r|s, a)，将括号内的数量乘以该概率，然后对所有可能性求和以获得期望值。方程是vπ的贝尔曼方程。它表达了一个状态与其后继状态值之间的关系。想象一下从状态s向前看，如图所示。每个空心圆表示一个状态，每个实心圆表示一个状态-动作对。从状态s开始，根节点在顶部，代理可以选择采取一些行动中的任何一个-如图所示的三个行动。对于每个行动，环境可以响应一个或多个下一个状态s0以及一个回报r。贝尔曼方程对所有可能性进行平均，将每个可能性的发生概率作为权重。它指出，起始状态的值必须等于（贴现的）预期下一个状态的值的总和，加上预期沿途获得的回报。值函数vπ是其贝尔曼方程的唯一解。

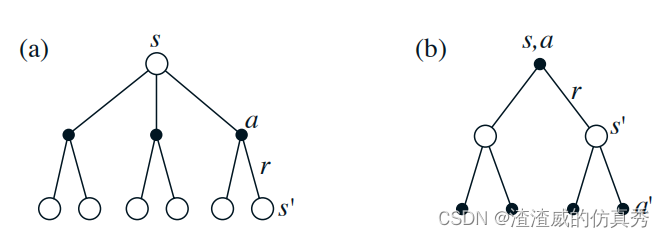
以上 是 (a) vπ 和 (b) qπ 的图表。

        这些图表通常用于展示强化学习中值函数的概念。其中，vπ 表示在给定策略 π 下，各个状态的值函数；qπ 则表示在给定策略 π 下，各个状态-动作对的值函数。

        在图表中，通常会为每个状态或状态-动作对绘制一个条形，并用该条形的高度来表示其在值函数中的值。对于 vπ，每个状态将有一个对应的条形，而对于 qπ，每个状态-动作对将有一个对应的条形。 这些图表可以帮助我们直观地理解强化学习中的值函数和策略迭代的过程。通过观察图表，我们可以清楚地看到各个状态或状态-动作对的值如何随着策略的迭代而逐渐变化。