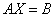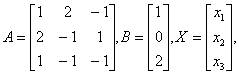我的服务原文访问:Camera
1.创建摄像机的坐标系,(创建原理,两条直线求其法向量)
Z轴:在世界坐标中指向摄像机的向量(D)
X轴:随便找一个向上量和Z向量求出的法向量就是X轴(R)
Y轴 :Z和X的法向量(U)
理解:如在一个2D的直角坐标系中x轴,y轴,在创建一个相对的直角坐标系,画一条直线a,在画一条垂直于直线a的垂线
b,则(a,b)就是一个坐标系,(a,b)就是摄像机。转换到3D也是一样。
2.把世界坐标经过转换矩阵变换到摄像机坐标

a.推到思想:参考 图形学:观察矩阵/LookUp矩阵的推导 - 知乎
摄像机坐标 = 世界坐标 x 旋转矩阵 x 位移矩阵
摄像机坐标 = 世界坐标 x VM (变换矩阵)
VM = RM * TM
TM :位移矩阵很简单,就是世界坐标指向相机坐标向量相反,很容易得到。
RM :旋转矩阵要矩阵的方程来计算,也旋转反向
3.摄像机位移说明,蓝色摄像机坐标
a1.世界坐标表示相机坐标,下图摄像机在世界坐标的a向量的地方
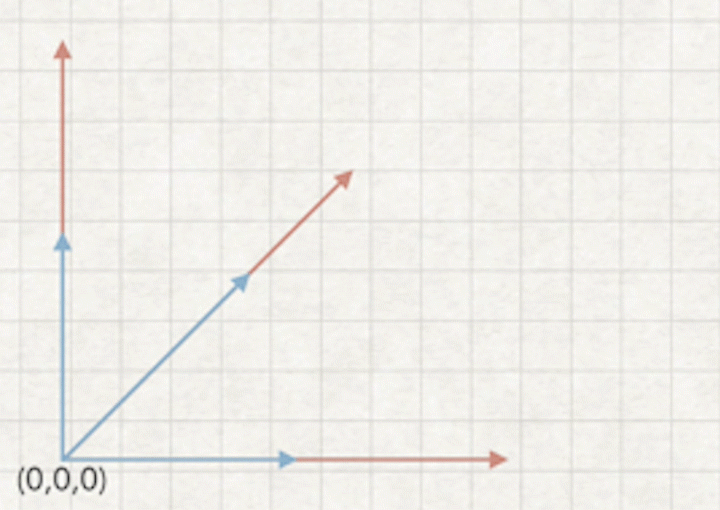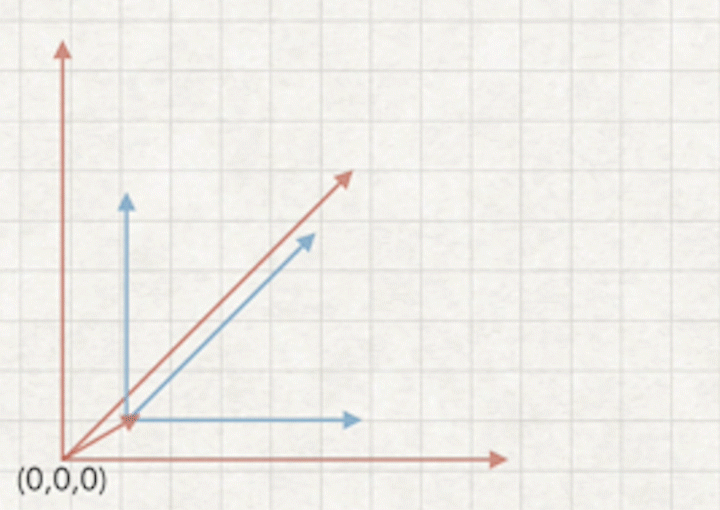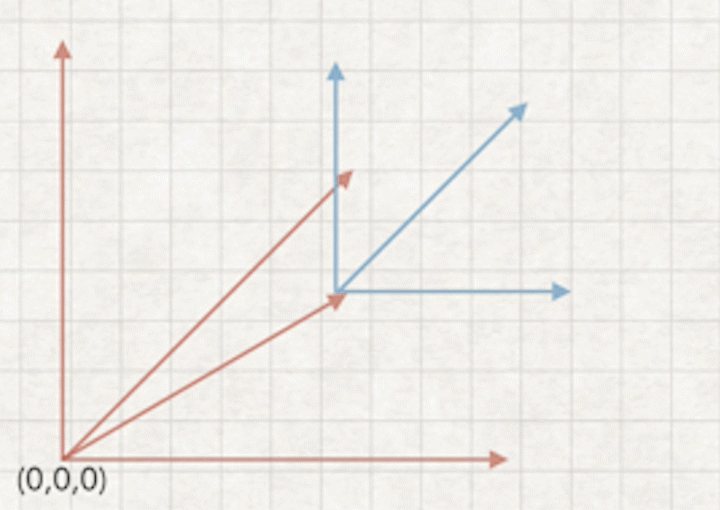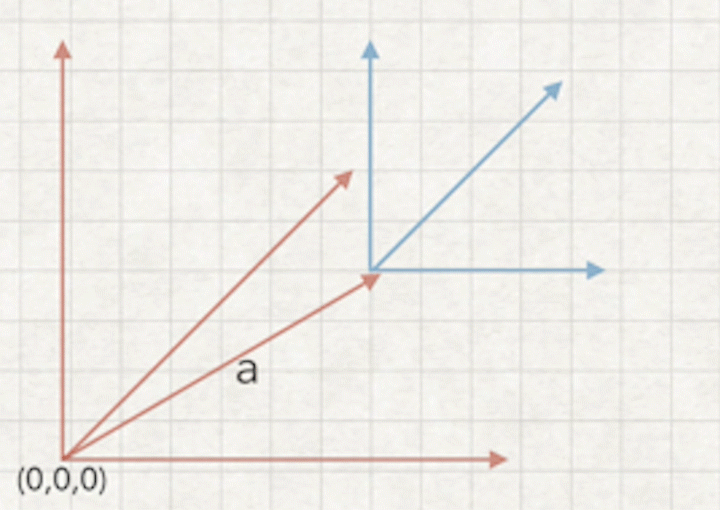
a2.摄像机坐标表示世界坐标,摄像机表示坐标世界坐标是a向量的相反向量
动画太大请问访问:https://stanserver.cn/image/gallery/2022_12_23_19_22_43_131.gif
a3.相当于摄像机不动,世界相对于摄像机相反方向移动,如下图
动画太大请问访问:https://stanserver.cn/image/gallery/2022_12_23_19_42_11_039.gif
求解摄像机位移坐标思想,是求解摄像机在世界坐标的反向量
4.摄像机旋转说明,蓝色摄像机坐标
a1.摄像机相对世界坐标旋转一个角度b
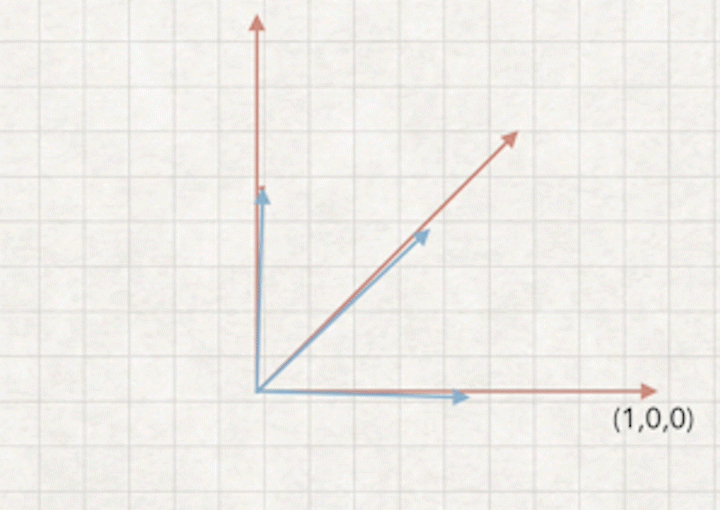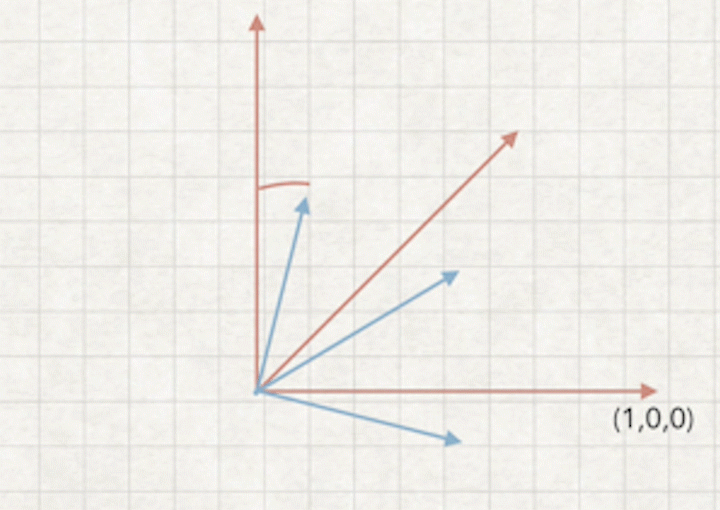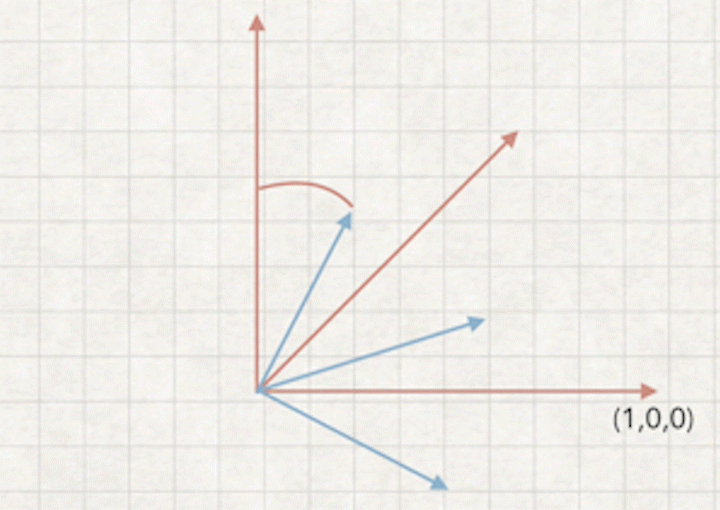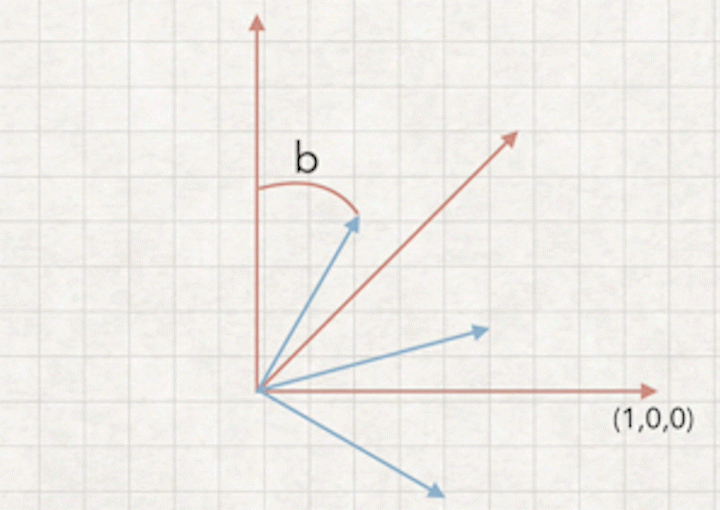
a2.摄像机坐标来看,相当于世界坐标旋转-b角度
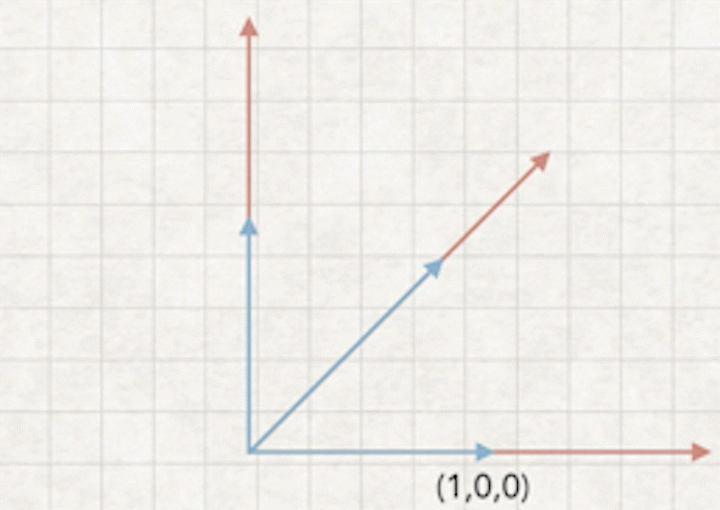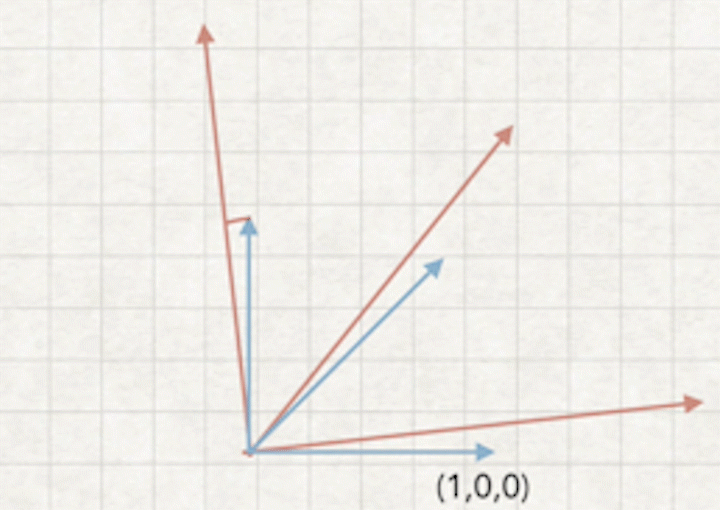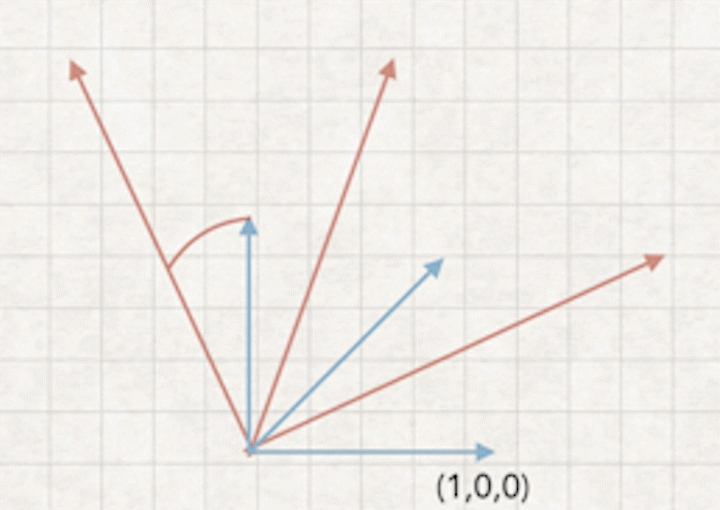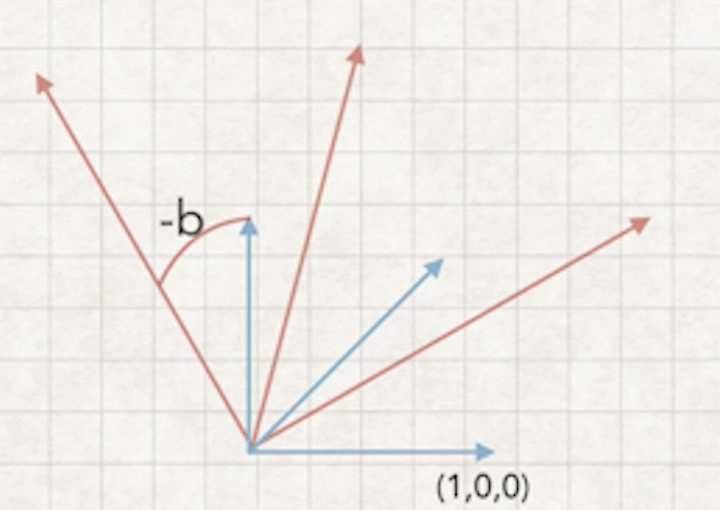
4.旋转矩阵推到过程
参考: 图形学:观察矩阵/LookUp矩阵的推导 - 知乎
p 6.6 逆矩阵
现设:
相机坐标原点和世界坐标原点重合没有位移,
WM世界坐标轴,并且向量单位向量矩阵
VM是摄像机的坐标轴,
RM未知旋转矩阵,使得WM世界坐标轴 和 VM是摄像机的坐标轴相等
如图:求旋转矩阵-b,相当于把摄像机坐标旋转到世界坐标(0,0,0)重合
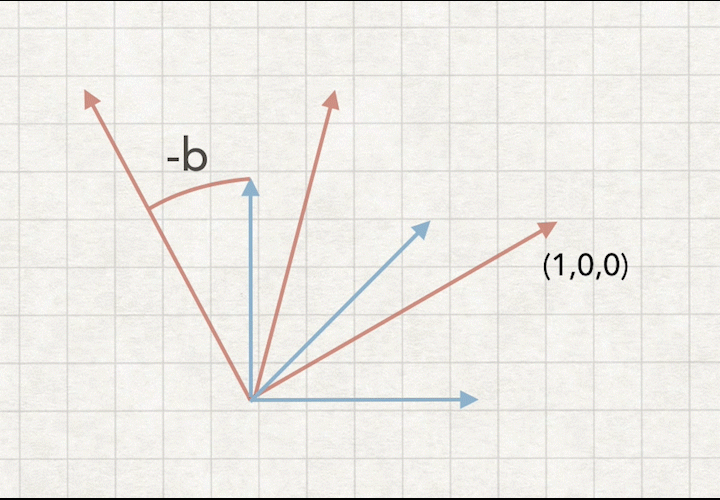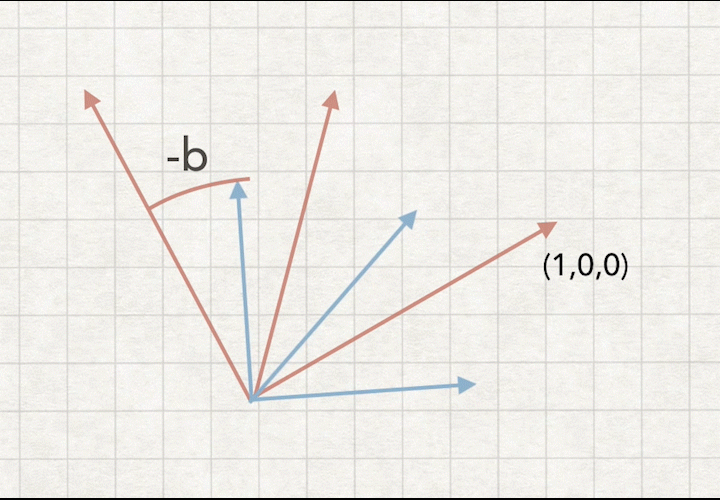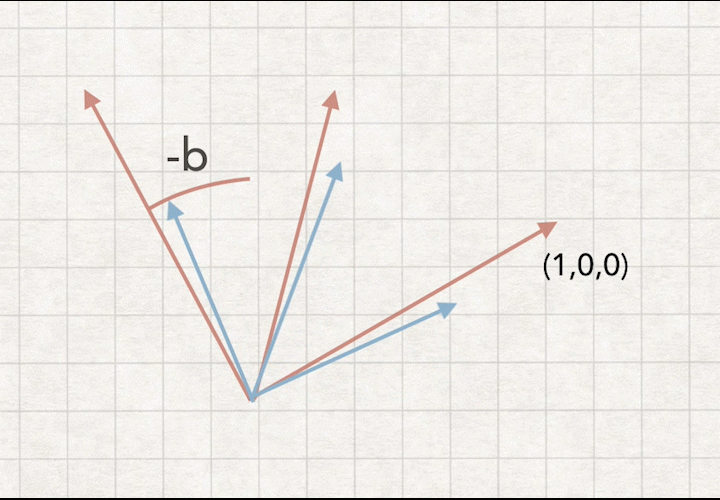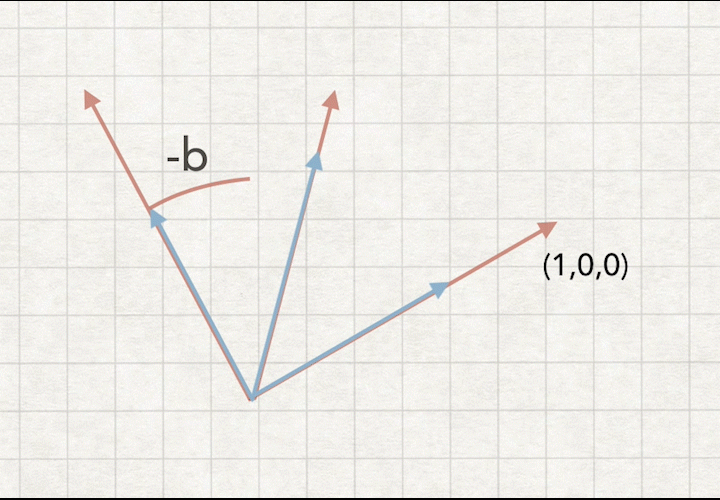
可得矩阵方程:
WM = RM * VM
两边同时右乘RM 的逆矩阵R-1M :
R-1M * WM = R-1M * RM * VM
(R-1M * RM )是单位矩阵,矩阵和单位矩阵相乘还是它本身,则有:
R-1M * WM = VM
因为WM 是单位矩阵,则有:
R-1M = VM
因为VM直角坐标系,他的逆矩阵等于他转置
RM = V-1M
结论:旋转变换矩阵就是摄像机矩阵的转置
5.gl代码书写
a.创建投影矩阵
//创建投影矩阵
glm::mat4 projection = glm::mat4(1.0f);//单位矩阵初始化
projection = glm::perspective(glm::radians(45.0f), (float)SCR_WIDTH / (float)SCR_HEIGHT, 0.1f, 100.0f);
ourShader.setMat4("projection", projection);b.一个摄像机位置,一个目标位置和一个表示世界空间中的上向量
//glm::LookAt函数需要一个位置、目标和上向量。它会创建一个和在上一节使用的一样的观察矩阵。
view = glm::lookAt(glm::vec3(camX, 0.0f, camZ),
glm::vec3(0.0f, 0.0f, 0.0f),
glm::vec3(0.0f, 1.0f, 0.0f));
ourShader.setMat4("view", view);c.把模型放到世界坐标系中
//把模型放到世界中 计算每个对象的模型矩阵,并在绘图前将其传递给着色器
glm::mat4 model = glm::mat4(1.0f);
model = glm::translate(model, cubePositions[i]);//模型位置
float angle = 20.0f * i;
model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));//模型旋转
ourShader.setMat4("model", model);
glDrawArrays(GL_TRIANGLES, 0, 36);6.Camera封装
a.观察者矩阵 前来两个向量确定方向向量,第三个参数是向上向量,方向和向上的向量计算摄像机的xyz轴
view = glm::lookAt(cameraPos, cameraPos + cameraFront, cameraUp);b.摄像机前后移动
cameraPos += cameraSpeed * cameraFront;
cameraPos -= cameraSpeed * cameraFront;c.摄像机左右移动 向量叉乘获得右轴
cameraPos -= glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;d.摄像机上下移动
cameraPos += cameraSpeed * cameraUp;
cameraPos -= cameraSpeed * cameraUp;e.摄像机俯仰左右旋转 计算方向向量的俯仰pitch和偏航yaw
现设方向向量的长度为“1”;如下图:
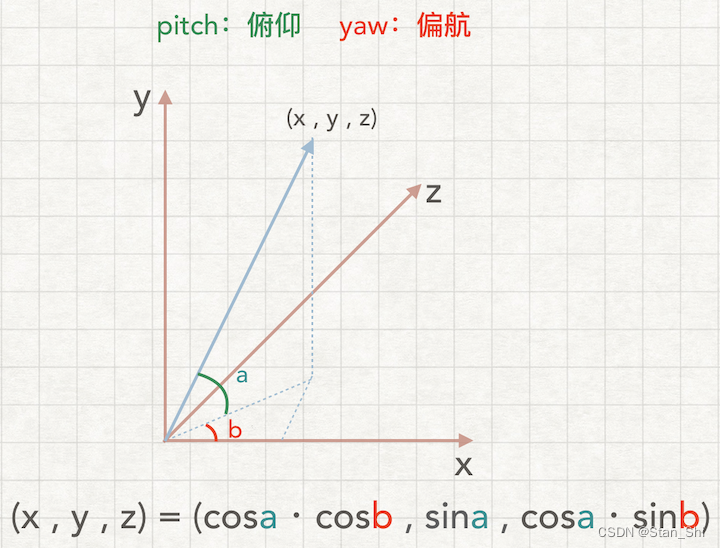
代码如下:
glm::vec3 front;
front.x = cos(glm::radians(Pitch)) * cos(glm::radians(Yaw));
front.y = sin(glm::radians(Pitch));
front.z = cos(glm::radians(Pitch)) * sin(glm::radians(Yaw));
Front = glm::normalize(front);//方向向量
//也重新计算右和向上向量 normalize归一化
Right = glm::normalize(glm::cross(Front, WorldUp)); //相机右轴
Up = glm::normalize(glm::cross(Right, Front)); //相机上轴f.缩放 Zoom调整透视投影矩阵的观察角
//创建投影矩阵
glm::mat4 projection = glm::mat4(1.0f);//单位矩阵初始化
projection = glm::perspective(glm::radians(camera.Zoom), (float)SCR_WIDTH / (float)SCR_HEIGHT, 0.1f, 100.0f);
ourShader.setMat4("projection", projection);8.矩阵方程 推导世界坐标到相机坐标的变换矩阵
|
1 、利用逆阵求解矩阵方程 (1) 设矩阵方程为
(2) 设矩阵方程为,是可逆方阵,即存在,在方程两边同时右乘,即得:,从而得方程组的解:,求出代入即可. (3) 设矩阵方程为,和均为可逆方阵,即和均存在,在方程两边同时左乘,右乘,即得:,从而得方程组的解:,求出和代入即可. |
2 、利用逆阵求解线性方程组(当方程个数和未知量个数相等时) 线性方程组可用矩阵方程
于是,当系数矩阵可逆,即存在时,在方程两边同时左乘,即得:,从而得到方程组的解:. 注:利用逆阵求解线性方程组是有条件的,首先系数矩阵必须是方阵,即方程组所含方程的个数与未知量的个数必须相等;其次系数矩阵还必须是可逆的.这和运用克莱姆法则解线性方程组的条件是一致的. |
典型例题 例6.6.6 解线性方程组 解 令
因为 故可逆,即存在, 因此, 即 也可进一步写出:. |
| 通过本节的学习,需要理解和掌握的是: (1) 方阵可逆的定义 (2) 判断方阵可逆的两个充要条件及其在解题中的应用 (3) 利用伴随矩阵求逆矩阵的公式 (4) 可逆方阵的性质 (5) 求方阵的逆阵在解矩阵方程和线性方程组中的应用. |
stanserver.cn