【贝叶斯回归】【第 2 部分】--推理算法

news2024/11/21 2:22:42

一、说明

        在第一部分中，我们研究了如何使用 SVI 对简单的贝叶斯线性回归模型进行推理。在本教程中，我们将探索更具表现力的指南以及精确的推理技术。我们将使用与之前相同的数据集。

二、模块导入

[1]:

%reset -sf

[2]:

import logging
import os

import torch
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from torch.distributions import constraints

import pyro
import pyro.distributions as dist
import pyro.optim as optim

pyro.set_rng_seed(1)
assert pyro.__version__.startswith('1.8.6')

[3]:

%matplotlib inline
plt.style.use('default')

logging.basicConfig(format='%(message)s', level=logging.INFO)
smoke_test = ('CI' in os.environ)
pyro.set_rng_seed(1)
DATA_URL = "https://d2hg8soec8ck9v.cloudfront.net/datasets/rugged_data.csv"
rugged_data = pd.read_csv(DATA_URL, encoding="ISO-8859-1")

三、贝叶斯线性回归

        我们的目标是再次根据数据集中的两个特征（该国家是否位于非洲及其地形坚固指数）来预测一个国家的人均 GDP 对数，但我们将探索更具表现力的指南。

3.1 模型+指南

       我们将再次写出模型，类似于第一部分，但明确不使用 PyroModule。我们将使用相同的先验写出回归中的每一项。 bA和bR是is_cont_africa和roughness对应的回归系数，a是截距，bAR是两个特征之间的相关因子。

        编写指南的过程与我们模型的构建非常相似，主要区别在于指南参数需要可训练。为此，我们使用在 ParamStore 中注册指南参数pyro.param()。注意尺度参数的正约束。

[4]:

def model(is_cont_africa, ruggedness, log_gdp):
    a = pyro.sample("a", dist.Normal(0., 10.))
    b_a = pyro.sample("bA", dist.Normal(0., 1.))
    b_r = pyro.sample("bR", dist.Normal(0., 1.))
    b_ar = pyro.sample("bAR", dist.Normal(0., 1.))
    sigma = pyro.sample("sigma", dist.Uniform(0., 10.))
    mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggedness
    with pyro.plate("data", len(ruggedness)):
        pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)

def guide(is_cont_africa, ruggedness, log_gdp):
    a_loc = pyro.param('a_loc', torch.tensor(0.))
    a_scale = pyro.param('a_scale', torch.tensor(1.),
                         constraint=constraints.positive)
    sigma_loc = pyro.param('sigma_loc', torch.tensor(1.),
                             constraint=constraints.positive)
    weights_loc = pyro.param('weights_loc', torch.randn(3))
    weights_scale = pyro.param('weights_scale', torch.ones(3),
                               constraint=constraints.positive)
    a = pyro.sample("a", dist.Normal(a_loc, a_scale))
    b_a = pyro.sample("bA", dist.Normal(weights_loc[0], weights_scale[0]))
    b_r = pyro.sample("bR", dist.Normal(weights_loc[1], weights_scale[1]))
    b_ar = pyro.sample("bAR", dist.Normal(weights_loc[2], weights_scale[2]))
    sigma = pyro.sample("sigma", dist.Normal(sigma_loc, torch.tensor(0.05)))
    mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggedness

[5]:

# Utility function to print latent sites' quantile information.
def summary(samples):
    site_stats = {}
    for site_name, values in samples.items():
        marginal_site = pd.DataFrame(values)
        describe = marginal_site.describe(percentiles=[.05, 0.25, 0.5, 0.75, 0.95]).transpose()
        site_stats[site_name] = describe[["mean", "std", "5%", "25%", "50%", "75%", "95%"]]
    return site_stats

# Prepare training data
df = rugged_data[["cont_africa", "rugged", "rgdppc_2000"]]
df = df[np.isfinite(df.rgdppc_2000)]
df["rgdppc_2000"] = np.log(df["rgdppc_2000"])
train = torch.tensor(df.values, dtype=torch.float)

3.2 SVI推理

        和之前一样，我们将使用 SVI 来执行推理。

[6]:

from pyro.infer import SVI, Trace_ELBO


svi = SVI(model,
          guide,
          optim.Adam({"lr": .05}),
          loss=Trace_ELBO())

is_cont_africa, ruggedness, log_gdp = train[:, 0], train[:, 1], train[:, 2]
pyro.clear_param_store()
num_iters = 5000 if not smoke_test else 2
for i in range(num_iters):
    elbo = svi.step(is_cont_africa, ruggedness, log_gdp)
    if i % 500 == 0:
        logging.info("Elbo loss: {}".format(elbo))

埃尔博损失：5795.467590510845
埃尔博损失：415.8169444799423
埃尔博损失：250.71916329860687
埃尔博损失：247.19457268714905
埃尔博损失：249.2004036307335
埃尔博损失：250.96484470367432
埃尔博损失：249.35092514753342
埃尔博损失：248.7831552028656
埃尔博损失：248.62140649557114
埃尔博损失：250.4274433851242

[7]:

from pyro.infer import Predictive


num_samples = 1000
predictive = Predictive(model, guide=guide, num_samples=num_samples)
svi_samples = {k: v.reshape(num_samples).detach().cpu().numpy()
               for k, v in predictive(log_gdp, is_cont_africa, ruggedness).items()
               if k != "obs"}

让我们观察模型中不同潜在变量的后验分布。

[8]:

for site, values in summary(svi_samples).items():
    print("Site: {}".format(site))
    print(values, "\n")

站点：a
       平均标准差 5% 25% 50% 75% 95%
0 9.177024 0.059607 9.07811 9.140463 9.178211 9.217098 9.27152

地点：bA
       平均标准差 5% 25% 50% 75% 95%
0 -1.890622 0.122805 -2.08849 -1.979107 -1.887476 -1.803683 -1.700853

站点：bR
       平均标准差 5% 25% 50% 75% 95%
0 -0.157847 0.039538 -0.22324 -0.183673 -0.157873 -0.133102 -0.091713

站点：bAR
       平均标准差 5% 25% 50% 75% 95%
0 0.304515 0.067683 0.194583 0.259464 0.304907 0.348932 0.415128

网站：西格玛
       平均标准差 5% 25% 50% 75% 95%
0 0.902898 0.047971 0.824166 0.870317 0.901981 0.935171 0.981577

3.3 HMC 

        与使用变分推理（为我们提供潜在变量的近似后验）相反，我们还可以使用马尔可夫链蒙特卡罗（MCMC）进行精确推理，这是一类算法，在极限情况下，允许我们从真实的样本中提取无偏样本。后部。我们将使用的算法称为 No-U Turn Sampler (NUTS) [1]，它提供了一种运行哈密顿蒙特卡罗的高效且自动化的方法。它比变分推理稍慢，但提供了精确的估计。

[9]:

from pyro.infer import MCMC, NUTS


nuts_kernel = NUTS(model)

mcmc = MCMC(nuts_kernel, num_samples=1000, warmup_steps=200)
mcmc.run(is_cont_africa, ruggedness, log_gdp)

hmc_samples = {k: v.detach().cpu().numpy() for k, v in mcmc.get_samples().items()}

样本：100%|██████████| 1200/1200 [00:30，38.99it/s，步长=2.76e-01，根据。概率=0.934]

[10]:

for site, values in summary(hmc_samples).items():
    print("Site: {}".format(site))
    print(values, "\n")

站点：a
       平均标准差 5% 25% 50% 75% 95%
0 9.182098 0.13545 8.958712 9.095588 9.181347 9.277673 9.402615

地点：bA
       平均标准差 5% 25% 50% 75% 95%
0 -1.847651 0.217768 -2.19934 -1.988024 -1.846978 -1.70495 -1.481822

站点：bR
       平均标准差 5% 25% 50% 75% 95%
0 -0.183031 0.078067 -0.311403 -0.237077 -0.185945 -0.131043 -0.051233

站点：bAR
       平均标准差 5% 25% 50% 75% 95%
0 0.348332 0.127478 0.131907 0.266548 0.34641 0.427984 0.560221

网站：西格玛
       平均标准差 5% 25% 50% 75% 95%
0 0.952041 0.052024 0.869388 0.914335 0.949961 0.986266 1.038723

3.4 比较后验分布

        让我们将通过变分推理获得的潜在变量的后验分布与哈密顿蒙特卡罗获得的潜在变量的后验分布进行比较。如下所示，对于变分推理，不同回归系数的边缘分布相对于真实后验（来自 HMC）而言是分散不足的。这是通过变分推理最小化的KL(q||p)损失（真实后验与近似后验的 KL 散度）的伪影。

        当我们绘制来自联合后验分布的不同横截面并覆盖来自变分推理的近似后验时，可以更好地看到这一点。请注意，由于我们的变分族具有对角协方差，因此我们无法对潜在变量之间的任何相关性进行建模，并且所得的近似值过于自信（分散不足）

[11]:

sites = ["a", "bA", "bR", "bAR", "sigma"]

fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 10))
fig.suptitle("Marginal Posterior density - Regression Coefficients", fontsize=16)
for i, ax in enumerate(axs.reshape(-1)):
    site = sites[i]
    sns.distplot(svi_samples[site], ax=ax, label="SVI (DiagNormal)")
    sns.distplot(hmc_samples[site], ax=ax, label="HMC")
    ax.set_title(site)
handles, labels = ax.get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');

_images/bayesian_regression_ii_18_0.png

[12]:

fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
fig.suptitle("Cross-section of the Posterior Distribution", fontsize=16)
sns.kdeplot(x=hmc_samples["bA"], y=hmc_samples["bR"], ax=axs[0], shade=True, label="HMC")
sns.kdeplot(x=svi_samples["bA"], y=svi_samples["bR"], ax=axs[0], label="SVI (DiagNormal)")
axs[0].set(xlabel="bA", ylabel="bR", xlim=(-2.5, -1.2), ylim=(-0.5, 0.1))
sns.kdeplot(x=hmc_samples["bR"], y=hmc_samples["bAR"], ax=axs[1], shade=True, label="HMC")
sns.kdeplot(x=svi_samples["bR"], y=svi_samples["bAR"], ax=axs[1], label="SVI (DiagNormal)")
axs[1].set(xlabel="bR", ylabel="bAR", xlim=(-0.45, 0.05), ylim=(-0.15, 0.8))
handles, labels = axs[1].get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');

_images/bayesian_regression_ii_19_0.png

3.5 多元正态指南

        与之前从对角正态指南获得的结果相比，我们现在将使用从多元正态分布的 Cholesky 分解生成样本的指南。这使我们能够通过协方差矩阵捕获潜在变量之间的相关性。如果我们手动编写此代码，我们将需要组合所有潜在变量，以便我们可以联合采样多元正态分布。

[13]:

from pyro.infer.autoguide import AutoMultivariateNormal, init_to_mean


guide = AutoMultivariateNormal(model, init_loc_fn=init_to_mean)

svi = SVI(model,
          guide,
          optim.Adam({"lr": .01}),
          loss=Trace_ELBO())

is_cont_africa, ruggedness, log_gdp = train[:, 0], train[:, 1], train[:, 2]
pyro.clear_param_store()
for i in range(num_iters):
    elbo = svi.step(is_cont_africa, ruggedness, log_gdp)
    if i % 500 == 0:
        logging.info("Elbo loss: {}".format(elbo))

埃尔博损失：703.0100790262222
埃尔博损失：444.6930855512619
埃尔博损失：258.20718491077423
埃尔博损失：249.05364602804184
埃尔博损失：247.2170884013176
埃尔博损失：247.28261297941208
埃尔博损失：246.61236548423767
埃尔博损失：249.86004841327667
埃尔博损失：249.1157277226448
埃尔博损失：249.86634194850922

我们再看一下后背的形状。您可以看到多变量指南能够捕获更多真实的后验信息。

[14]:

predictive = Predictive(model, guide=guide, num_samples=num_samples)
svi_mvn_samples = {k: v.reshape(num_samples).detach().cpu().numpy()
                   for k, v in predictive(log_gdp, is_cont_africa, ruggedness).items()
                   if k != "obs"}
fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 10))
fig.suptitle("Marginal Posterior density - Regression Coefficients", fontsize=16)
for i, ax in enumerate(axs.reshape(-1)):
    site = sites[i]
    sns.distplot(svi_mvn_samples[site], ax=ax, label="SVI (Multivariate Normal)")
    sns.distplot(hmc_samples[site], ax=ax, label="HMC")
    ax.set_title(site)
handles, labels = ax.get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');

_images/bayesian_regression_ii_23_0.png

        现在让我们比较对角法线引导和多元法线引导计算的后验。请注意，多元分布比对角正态分布更不均匀。

[15]:

fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
fig.suptitle("Cross-sections of the Posterior Distribution", fontsize=16)
sns.kdeplot(x=svi_samples["bA"], y=svi_samples["bR"], ax=axs[0], label="SVI (Diagonal Normal)")
sns.kdeplot(x=svi_mvn_samples["bA"], y=svi_mvn_samples["bR"], ax=axs[0], shade=True, label="SVI (Multivariate Normal)")
axs[0].set(xlabel="bA", ylabel="bR", xlim=(-2.5, -1.2), ylim=(-0.5, 0.1))
sns.kdeplot(x=svi_samples["bR"], y=svi_samples["bAR"], ax=axs[1], label="SVI (Diagonal Normal)")
sns.kdeplot(x=svi_mvn_samples["bR"], y=svi_mvn_samples["bAR"], ax=axs[1], shade=True, label="SVI (Multivariate Normal)")
axs[1].set(xlabel="bR", ylabel="bAR", xlim=(-0.45, 0.05), ylim=(-0.15, 0.8))
handles, labels = axs[1].get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');

_images/bayesian_regression_ii_25_0.png

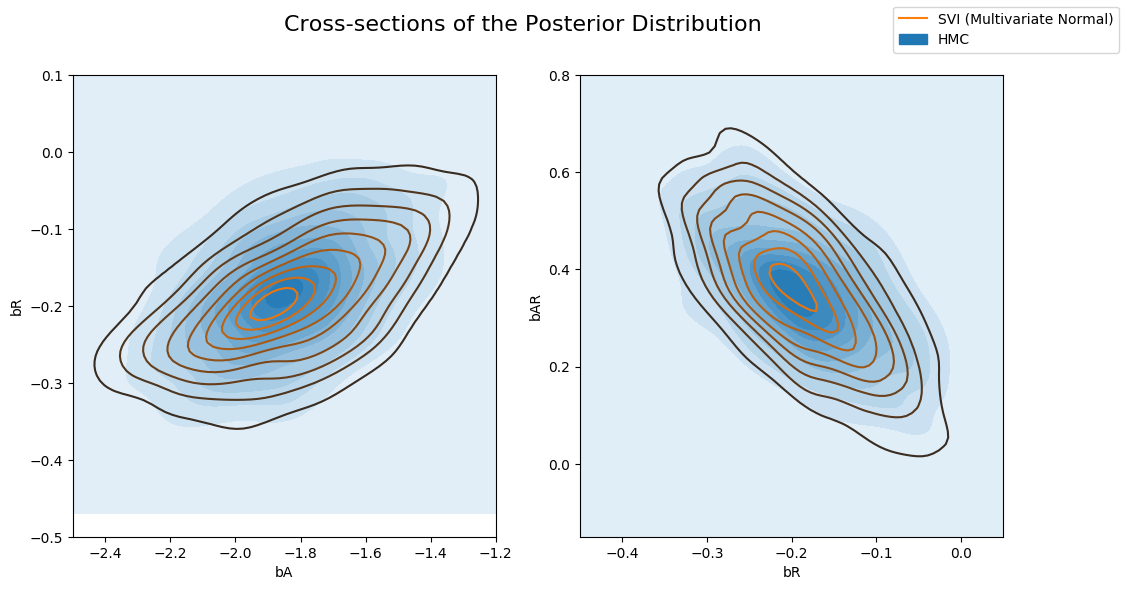
        以及由 HMC 计算后验的多变量指南。请注意，多变量指南可以更好地捕获真实的后验。

[16]:

fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
fig.suptitle("Cross-sections of the Posterior Distribution", fontsize=16)
sns.kdeplot(x=hmc_samples["bA"], y=hmc_samples["bR"], ax=axs[0], shade=True, label="HMC")
sns.kdeplot(x=svi_mvn_samples["bA"], y=svi_mvn_samples["bR"], ax=axs[0], label="SVI (Multivariate Normal)")
axs[0].set(xlabel="bA", ylabel="bR", xlim=(-2.5, -1.2), ylim=(-0.5, 0.1))
sns.kdeplot(x=hmc_samples["bR"], y=hmc_samples["bAR"], ax=axs[1], shade=True, label="HMC")
sns.kdeplot(x=svi_mvn_samples["bR"], y=svi_mvn_samples["bAR"], ax=axs[1], label="SVI (Multivariate Normal)")
axs[1].set(xlabel="bR", ylabel="bAR", xlim=(-0.45, 0.05), ylim=(-0.15, 0.8))
handles, labels = axs[1].get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');

_images/bayesian_regression_ii_27_0.png

参考

[1] 霍夫曼、马修·D.和安德鲁·格尔曼。“禁止掉头采样器：在哈密顿蒙特卡罗中自适应设置路径长度。” 机器学习研究杂志 15.1（2014）：1593-1623。https://arxiv.org/abs/1111.4246。

以前的 下一个

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1149442.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

亮氨酸脯氨酸肽——一种新型的医药中间体研究肽

亮氨酸脯氨酸肽——一种新型的医药中间体研究肽

亮氨酸脯氨酸医药中间体肽是一种合成（人造）激素，类似于大脑中产生的天然激素。它用于治疗许多医疗问题，包括： 子宫平滑肌瘤（子宫肌瘤）出血引起的贫血，或晚期或晚期前列腺癌症&#…
阅读更多...
管理类联考——数学——汇总篇——知识点突破——代数——整式分式——记忆

管理类联考——数学——汇总篇——知识点突破——代数——整式分式——记忆

文章目录 考点记忆/考点汇总——按大纲 整体目录大纲法记忆宫殿法绘图记忆法 局部数字编码法归类记忆法重点记忆法歌决记忆法谐音记忆法理解记忆法比较记忆法转图像记忆法可视化法 本篇思路：根据各方的资料，比如名师的资料，按大纲或者其他方式…
阅读更多...
大数据之LibrA数据库系统告警处理（ALM-12002 HA资源异常）

大数据之LibrA数据库系统告警处理（ALM-12002 HA资源异常）

告警解释 HA软件周期性检测Manager的WebService浮动IP地址和数据库。当HA软件检测到浮动IP地址或数据库异常时，产生该告警。 当HA检测到浮动IP地址或数据库正常后，告警恢复。 告警属性 告警参数 对系统的影响 如果Manager的WebService浮动IP地址异常…
阅读更多...
手机平板摄像头如何给电脑用来开视频会议

手机平板摄像头如何给电脑用来开视频会议

环境： Iriun Webcam EV虚拟摄像头 钉钉会议 问题描述： 手机平板摄像头如何给电脑用来开视频会议 解决方案： 1.下载软件 手机端和电脑端都下载这个软件，连接同一局域网打开软件连接好 另外一款软件Iriun 也是一样操作 2.打…
阅读更多...
Pytorch L1,L2正则化

Pytorch L1,L2正则化

L1正则化和L2正则化是常用的正则化技术，用于在机器学习模型中控制过拟合。它们的主要区别在于正则化项的形式和对模型参数的影响。 L1正则化（Lasso正则化）： 正则化项形式：L1正则化使用模型参数的绝对值之和作为正则化…
阅读更多...
RUP核心工作流2021-架构师（六十四）

RUP核心工作流2021-架构师（六十四）

1、根据传统的软件生命周期方法学，可以把软件生命周期划分为（）。 A、软件定义、软件开发、软件测试、软件维护 B、软件定义、软件开发、软件运行、软件维护 C、软件分析、软件设计、软件开发、软件维护 D、需求获取、软件设计、软件开发、…
阅读更多...
跳槽一定用得上的大厂Java题库！

跳槽一定用得上的大厂Java题库！

2023年已经接近尾声了，疫情的影响也在逐渐减小，市场慢慢复苏。不过最近还是会有一些读者粉丝朋友反馈，“Java市场饱和了”、“大环境还是不好”、“投几十个简历都没有一个约面的”。其实并不是岗位需求量变少了，是越来越多的公司…
阅读更多...
Calcite 优化层详解

Calcite 优化层详解

1、关系代数与火山模型 1）关系代数 基本的关系代数运算有选择、投影、集合并、集合差、笛卡儿积等。 在这些基本运算之外，还有一些集合之间的交集、连接、除和赋值等运算。 连接运算可分为连接、等值连接、自然连接、外连接、左外连接和右外连接。 …
阅读更多...
腰背肌筋膜炎能彻底治愈吗

腰背肌筋膜炎能彻底治愈吗

腰背肌筋膜炎：急性期腰部疼痛剧烈，有烧灼感，腰部活动时症状加重，局部压痛显著，有时体温升高、血液检查可见白细胞增高。急性发作后，少数患者症状完全消退，多数会遗留疼痛，或相隔数月…
阅读更多...
SSM律师事务所业务管理系统 毕业设计-附源码01664

SSM律师事务所业务管理系统 毕业设计-附源码01664

摘 要 随着科学技术的飞速发展，社会的方方面面、各行各业都在努力与现代的先进技术接轨，通过科技手段来提高自身的优势，律师事务所业务管理系统当然也不能排除在外。律师事务所业务管理系统是以实际运用为开发背景，运用软件工程原…
阅读更多...
QT实现在线流媒体播放平台

QT实现在线流媒体播放平台

文章目录 QT实现在线流媒体播放平台简介开发视频ffmpeg下载SimpleVideoPlayer.hSimpleVideoPlayer.cpp 开发音频添加功能打开文件夹播放暂停播放上下一首选择倍速 效果展示项目下载 QT实现在线流媒体播放平台 简介 Qt是一种流行的C开发框架，它提供了用于构建图形用…
阅读更多...
基于 Center 的 3D 目标检测和跟踪

基于 Center 的 3D 目标检测和跟踪

论文地址：https://arxiv.org/abs/2006.11275 论文代码：https://github.com/tianweiy/CenterPoint 3D 目标通常表示为点云中的 3D Boxes。 CenterPoint 在第一阶段，使用关键点检测器检测对象的中心，然后回归到其他属性&#xff0…
阅读更多...
【骑行探秘】穿越海晏村，揭秘贝丘渔场的神秘面纱

【骑行探秘】穿越海晏村，揭秘贝丘渔场的神秘面纱

在这个阳光明媚的周末，我们校长骑行群一行人骑着自行车，从大观公园门口出发，开始了一段别开生面的骑行之旅。沿途我们将穿越草海隧道湿地公园、迎海路、海埂公园西门（第二集合点）、宝丰湿地公园、斗南湿地公园、蓝光城…
阅读更多...
二叉排序树c语言版

二叉排序树c语言版

1、定义二叉树数据域、二叉树结点 /*** 二叉树节点数据 */ typedef struct treenodedata {int sort;char* name;} TreeNodeData;/**** 二叉树节点定义 */ typedef struct binarytree {/*** 结点数据域*/TreeNodeData* data;/**左子树*/struct binarytree* leftChild;/**左子树…
阅读更多...
双11满减大促，直播间1折抢购！

双11满减大促，直播间1折抢购！

你是知道的，双11本来是光棍节！ 2009年，阿里掀起了一场网络促销活动，光棍节从此成了全民的购物节！ 从2009年到2021年，阿里双11当天的交易额，从仅有的0.5亿猛增至5403亿，以惊人的速度…
阅读更多...
【人口数据集总结】WorldPop、GWPv4等

【人口数据集总结】WorldPop、GWPv4等

1 全球人口数据WorldPop 数据详解可参见另一博客-【数据集8】全球人口数据WorldPop详解。 WorldPop是由南安普顿大学在2013年10月发起的全球人口数据评估，将AfriPop，AsiaPop和AmeriPop人口调查项目整合到一起。数据集已经被众多的组织和机构使用：联合国开发计划署，联合国…
阅读更多...
实例教程：如何在应用中集成美狐直播美颜SDK

实例教程：如何在应用中集成美狐直播美颜SDK

随着直播和视频应用的兴起，用户对于视频质量和外貌自然度的要求越来越高。为了满足这一需求，开发者们可以通过集成直播美颜SDK来提供更吸引人的视频体验。本文将为您提供一个实例教程，以演示如何在您的应用中成功集成直播美颜SDK。无论您是一…
阅读更多...
Plant Physiology：DAP-seq助力揭示YABBY11转录因子调控杨树叶形自然变异的分子机制

Plant Physiology：DAP-seq助力揭示YABBY11转录因子调控杨树叶形自然变异的分子机制

2023年3月，北京林业大学生物学院宋跃朋教授课题组的研究成果发表在了Plant Physiology期刊上（影响因子7.4），文章题目为 “Enhanced genome-wide association reveals the role of YABBY11-NGATHA-LIKE1 in leaf serration develop…
阅读更多...
win10 javaweb 项目8080端口被占用

win10 javaweb 项目8080端口被占用

文章目录 前言出现场景：解决思路： 前言 提示：生活该走向何处？也许你还不知道答案，但是你一定是答案的一部分。 出现场景： 解决思路： 找到运行的进程直接干掉 打开命令窗口（win r…
阅读更多...
3.1每日一题（定积分求压力问题）

3.1每日一题（定积分求压力问题）

公式： (1) 压力等于压强乘以面积 (2) 压强等于ρgh(即密度，重力加速度，水的深度) 注：题目表面不一样，实际的原理都一样，做透一道题等于做懂一类题
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023