L1正则化和L2正则化是常用的正则化技术,用于在机器学习模型中控制过拟合。它们的主要区别在于正则化项的形式和对模型参数的影响。
L1正则化(Lasso正则化):
- 正则化项形式:L1正则化使用模型参数的绝对值之和作为正则化项,即L1范数。
- 影响模型参数:L1正则化倾向于将一些模型参数压缩为0,从而实现特征选择和稀疏性。因此,它可以用于特征选择和模型简化。
- 其他特点:由于L1正则化的非光滑性,优化问题在参数接近零时更容易找到解,因此它对于具有大量无关特征的问题更有效。
L2正则化(Ridge正则化):
- 正则化项形式:L2正则化使用模型参数的平方和作为正则化项,即L2范数。
- 影响模型参数:L2正则化倾向于使模型参数趋向于较小的值,但不会将其完全压缩为零。它通过减小模型参数的绝对值来控制参数的大小。
- 其他特点:L2正则化是光滑的,优化问题在参数接近零时相对平滑,因此对于许多问题都能得到较好的结果。
总结:
- L1正则化倾向于稀疏性和特征选择,适用于具有大量无关特征的问题。
- L2正则化倾向于模型参数较小,适用于控制模型复杂度和减少过拟合。
- 在某些情况下,可以同时使用L1和L2正则化形成弹性网络(Elastic Net),综合了两者的优点。
选择使用L1正则化还是L2正则化取决于具体问题和数据集的特点。通常建议先尝试L2正则化,如果模型仍然过拟合或需要进行特征选择,则可以考虑使用L1正则化。
对L1产生稀疏权值和L2产生平滑权值的理解
L1的定义是L1 = |w1| + |w2| + |w3| + ... + |wn|
L2的定义是L2 = w1^2 + w2^2 + w3^2 + ... + wn^2
L1和L2分别对w求导可得
dL1/dw = sign(wi)
dL2/dw = wi
假设wi为某个大于零的浮点数,学习率lr为0.5,根据梯度下降算法,
L1的权值更新方式为wi = wi - lr*(dL1/dw) = wi - lr*1 = wi - 0.5
L2的权值更新方式为wi = wi - lr*(dL2/dw) = wi - lr*wi = wi - 0.5wi
可以看出,L1每次更新都是减去一个固定的值,那就可能在多次迭代之后,权值为0的情况
而L2虽然权值也在减小,但是总不为0
需要注意的是,通常情况下,我们更倾向于对权值进行正则化,而不是对偏置进行正则化的原因有以下几点:
-
偏置的作用:偏置(bias)是模型中的一个常数项,它的作用是调整模型预测值与实际值之间的偏差。偏置通常用来解决模型在数据特征上的平移问题,而不会引入过多的复杂性。由于偏置只是一个常数,它的取值并不像权值那样会随着训练过程而变化,因此对偏置进行正则化对于控制模型的复杂度影响较小。
-
影响模型容量:正则化的目的是通过限制参数的取值范围来控制模型的复杂度,避免过拟合。权值在模型中起到了控制特征的重要作用,对权值进行正则化可以有效地减少模型的复杂度,提高泛化能力。而偏置的作用相对较小,对偏置进行正则化往往对模型的泛化能力影响较小。
-
数据中的偏移:在实际的数据中,通常会存在一些偏移(bias),即使我们对权值不进行正则化,模型也可以通过调整偏置来适应这种偏移。因此,对偏置进行正则化可能会导致对数据中的偏移进行过度拟合,而忽略了模型对其他特征的学习能力。
测试代码如下
import torch
import matplotlib.pyplot as plt
torch.manual_seed(25)
x_train = torch.tensor([1,2,3,4,5,6,7,8,9,10],dtype=torch.float32).unsqueeze(-1)
y_train = torch.tensor([0.52,8.54,6.94,20.76,32.17,30.65,40.46,80.12,75.12,98.83],dtype=torch.float32).unsqueeze(-1)
plt.scatter(x_train.detach().numpy(),y_train.detach().numpy(),marker='o',s=50,c='r')
class Linear(torch.nn.Module):
def __init__(self):
super().__init__()
self.layers = torch.nn.Sequential(
torch.nn.Linear(in_features=1, out_features=3),
torch.nn.Sigmoid(),
torch.nn.Linear(in_features=3,out_features=5),
torch.nn.Sigmoid(),
torch.nn.Linear(in_features=5, out_features=10),
torch.nn.Sigmoid(),
torch.nn.Linear(in_features=10,out_features=5),
torch.nn.Sigmoid(),
torch.nn.Linear(in_features=5, out_features=1),
torch.nn.ReLU(),
)
def forward(self,x):
return self.layers(x)
linear = Linear()
opt = torch.optim.Adam(linear.parameters(),lr= 0.005)
loss_fn = torch.nn.MSELoss()
for epoch in range(1000):
for iter in range(10):
L1 = 0
L2 = 0
for name,param in linear.named_parameters():
if 'bias' not in name:
L1 += torch.norm(param, p=1) * 1e-3
L2 += torch.norm(param, p=2) * 1e-3
opt.zero_grad()
output = linear(x_train[iter])
loss = loss_fn(output, y_train[iter]) + L1 + L2
loss.backward()
opt.step()
if __name__ == '__main__':
predict_loss = 0
for i in range(1000):
x = torch.tensor([i/100], dtype=torch.float32)
y_predict = linear(x)
plt.scatter(x.detach().numpy(),y_predict.detach().numpy(),s=2,c='b')
plt.scatter(i/100,i*i/10000,s=2,c='y')
predict_loss = (i*i/10000 - y_predict)**2/(y_predict)**2 + predict_loss
plt.show()
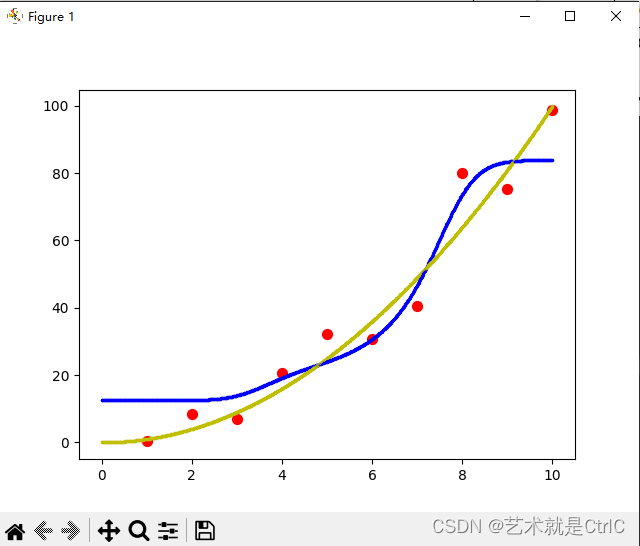
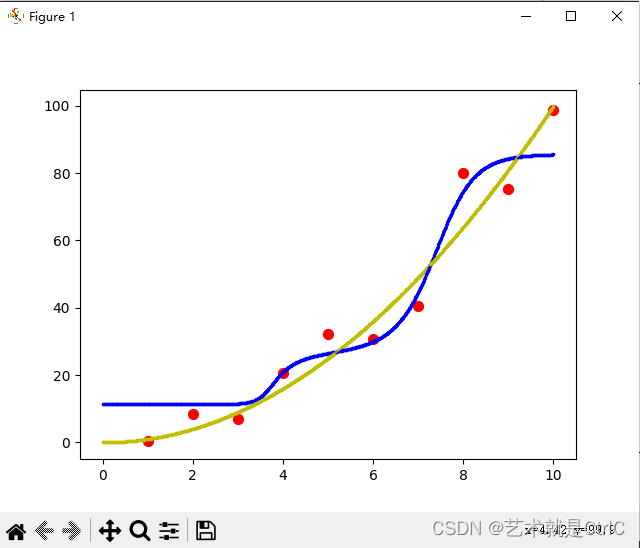
不使用L1,L2正则化的情况如下
只使用L1正则化的情况如下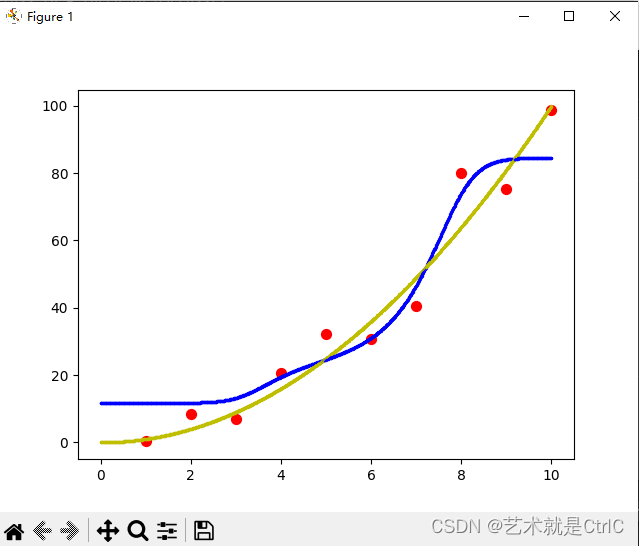
只使用L2正则化的情况如下
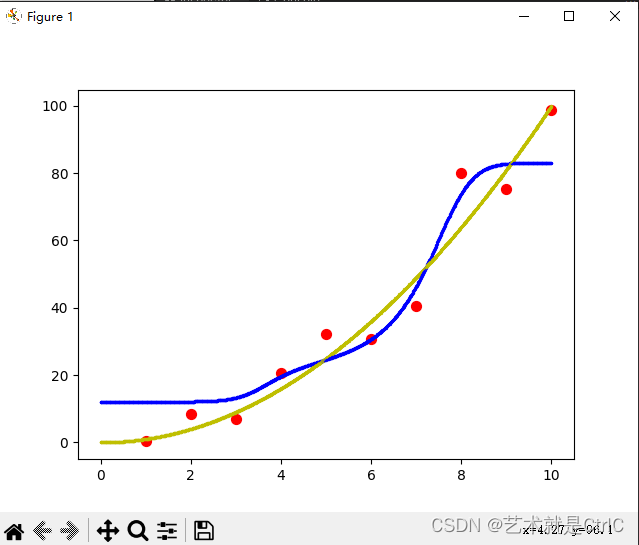
同时使用L1和L2正则化的情况如下