B题完整解答过程
- 写在最后
- 技术文档(部分)
- 问题分析
- 假设
- 符号说明
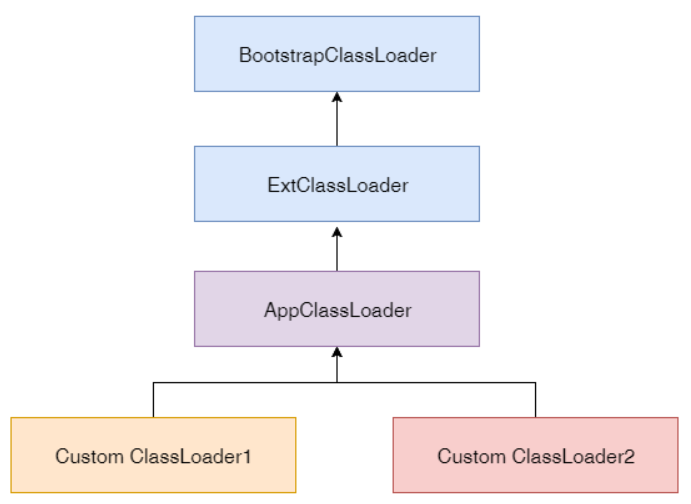
- 1 基于自适应ARIMA-LR模型的需求量预测(问题一第一小问)
- 1.1 ARIMA模型的建立
- 1.2 LR模型的建立
- 1.3 自适应混合ARIMA-LR模型的建立
- 1.4 ARIMA模型的求解
- 1.5 LR模型的求解
- 代码(部分)
- 第一问
- Q1_1.m
- Q1_2.m
- Q1_3_main.m
- Q1_4.m
- Q1_5.m
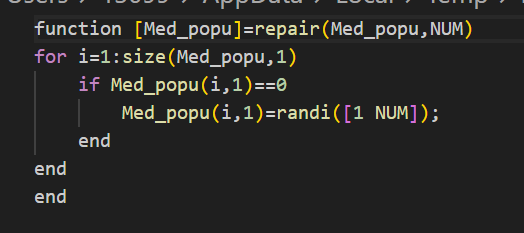
- repair.m
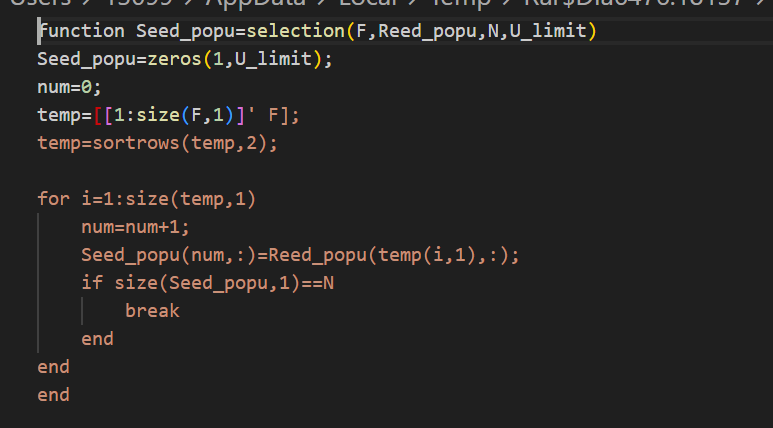
- selection.m
- 结果
- 完整
- Q1
- Q2
- Q3
写在最后
经过整整一天半的时间,B题全部解答过程已经完成啦,包括完整的代码与运行结果,还有分析目文档,欢迎大家交流讨论~
技术文档(部分)
问题分析
对于问题一,首先题目要求预测出各商家在各仓库的商品2023-05-16至2023-05-30的需求量。在大框架下,该问题属于一个时间序列预测问题。可以采用AR、MA、ARIMA等模型进行预测。但是序列中存在一定的突发性波动或是非线性规律,故考虑采用混合模型对需求量进行预测。可以根据某一段时期的预测准确度评价所设计的算法的优越性。同时,也可以根据在测试集中的预测准确度计算混合模型的混合权重,达到自适应的目的。
在对序列进行预测后,题目要求对时间序列进行分类,其实是需要确定分类的依据指标。对于该问可以先确立一系列候选指标,然后采用智能优化算法以最大化组内相似度为目的对分类指标的选取进行优化。
对于问题二,题目要求对新出现的商家+仓库+商品维度的预测维度进行预测。求解该问题时,应先提取该序列的特征,通过与已有序列进行两阶段匹配。在第一阶段,通过第一问所选取的分类指标确定较为接近的序列组;在第二阶段,通过具体的相似度选取最为相似的序列。此时,可以对选取的序列进行调整后与新序列进行拼接,再通过第一问所设计的算法对新序列进行预测。
对于问题三,题目要求对大型促销期间(2023-06-01至2023-06-20)的需求量数据进行预测。对于该问题,可以先提取出去趋势波动,其中趋势可用一次回归进行表征。然后用回归模型对待预测序列进行预测,再在预测值的基础上叠加波动项,形成最后大型促销期间的最终预测值
假设
1、假设市场价格完全由供需关系决定,不受政策管控影响。
2、假设不出现突发不可抗灾害导致的销售量爆发等情况的发生。
3、假设供应链关系大体稳定不变。
符号说明

1 基于自适应ARIMA-LR模型的需求量预测(问题一第一小问)
1.1 ARIMA模型的建立

1.2 LR模型的建立

1.3 自适应混合ARIMA-LR模型的建立
对于每一预测算法,均通过部分序列作为测试集。本文所设计的混合算法的混合思想主要为:在往期的预测中性能越好则在未来的预测中的权重就越高,对预测值的贡献度就越高。

1.4 ARIMA模型的求解

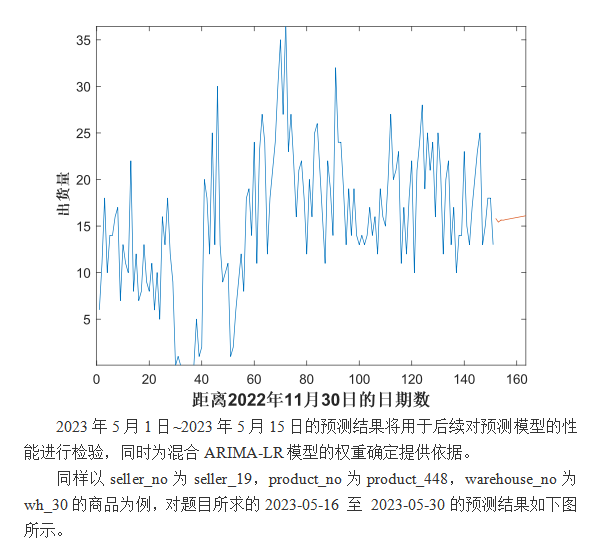
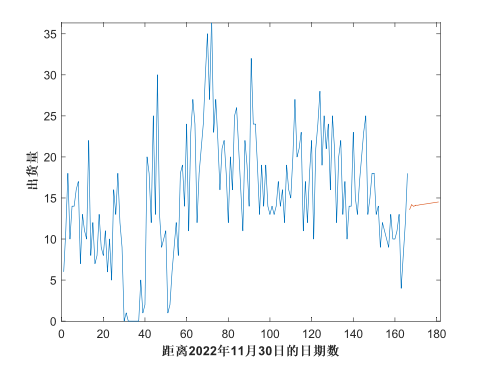
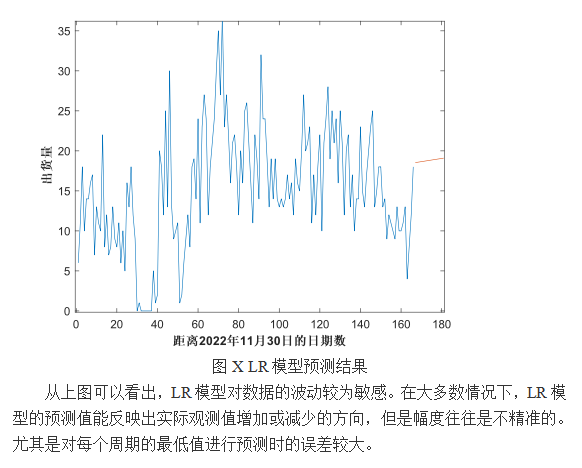
从上图中可以看出,ARIMA模型大致描述出了出货量的趋势走向及部分波动。但是仍有许多波动没有在预测中被反应出来,仍需进一步改进。
1.5 LR模型的求解

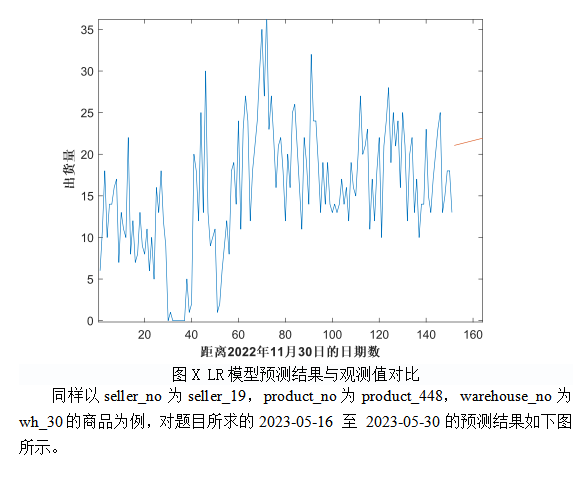
代码(部分)
第一问
Q1_1.m
Q1_2.m
Q1_3_main.m
Q1_4.m
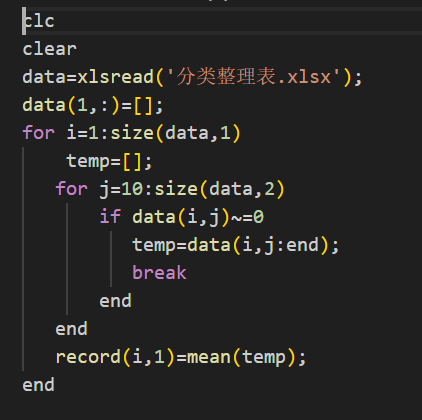
Q1_5.m
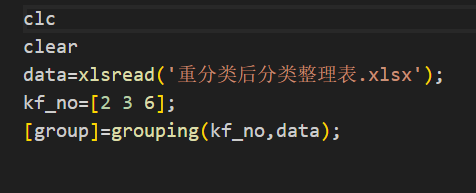
repair.m
selection.m
结果
完整
Q1
Q2

Q3