mv 命令（move 的缩写），既可以在不同的目录之间移动文件或目录，也可以对文件和目录进行重命名。该命令的基本格式如下：

[root@localhost ~]# mv 【选项】 源文件 目标文件

• -f：强制覆盖，如果目标文件已经存在，则不询问，直接强制覆盖；

• -i：交互移动，如果目标文件已经存在，则询问用户是否覆盖（默认选项）；

• -n：如果目标文件已经存在，则不会覆盖移动，而且不询问用户；

• -v：显示文件或目录的移动过程；

• -u：若目标文件已经存在，但两者相比，源文件更新，则会对目标文件进行升级；

需要注意的是，同 rm 命令类似，mv 命令也是一个具有破坏性的命令，如果使用不当，很可能给系统带来灾难性的后果。

【例 1】移动文件或目录。

[root@localhost ~]# mv cangls /tmp
#移动之后，源文件会被删除，类似剪切
[root@localhost ~]# mkdir movie
[root@localhost ~]# mv movie/ /tmp
#也可以移动目录。和 rm、cp 不同的是，mv 移动目录不需要加入 "-r" 选项

如果移动的目标位置已经存在同名的文件，则同样会提示是否覆盖，因为 mv 命令默认执行的也是 "mv -i" 的别名，例如：

[root@localhost ~]# touch cangls
#重新建立文件
[root@localhost ~]# mv cangls /tmp
mv:县否覆盖"tmp/cangls"？y
#由于 /tmp 目录下已经存在 cangls 文件，所以会提示是否覆盖，需要手工输入 y 覆盖移动

【例 2】强制移动。之前说过，如果目标目录下已经存在同名文件，则会提示是否覆盖，需要手工确认。这时如果移动的同名文件较多，则需要一个一个文件进行确认，很不方便。如果我们确认需要覆盖已经存在的同名文件，则可以使用 "-f" 选项进行强制移动，这就不再需要用户手工确认了。例如：

[root@localhost ~]# touch cangls
#重新建立文件
[root@localhost ~]# mv -f cangls /tmp
#就算 /tmp/ 目录下已经存在同名的文件，由于"-f"选项的作用，所以会强制覆盖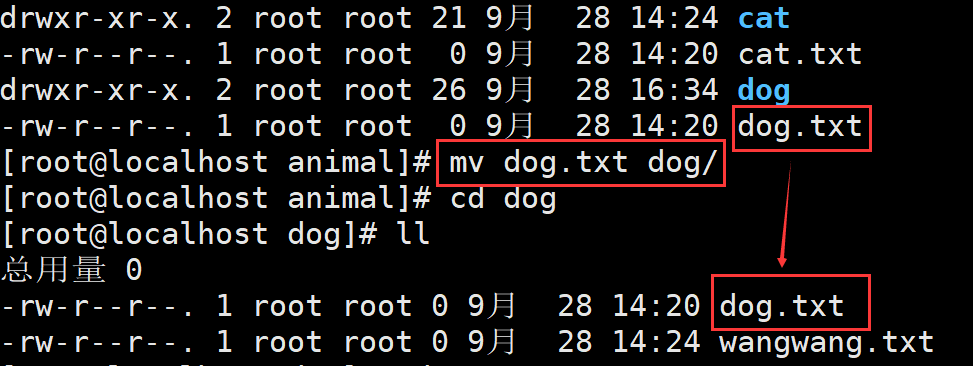

【例 3】不覆盖移动。既然可以强制覆盖移动，那也有可能需要不覆盖的移动。如果需要移动几百个同名文件，但是不想覆盖，这时就需要 "-n" 选项的帮助了。例如：

[root@localhost ~]# ls /tmp
/tmp/bols /tmp/cangls
#在/tmp/目录下已经存在bols、cangls文件了
[root@localhost ~]# mv -vn bols cangls lmls /tmp/、
"lmls"->"/tmp/lmls"
#再向 /tmp/ 目录中移动同名文件，如果使用了 "-n" 选项，则可以看到只移动了 lmls，而同名的 bols 和 cangls 并没有移动（"-v" 选项用于显示移动过程）

【例 4】改名。如果源文件和目标文件在同一目录中，那就是改名。例如：

[root@localhost ~]# mv bols lmls
#把 bols 改名为 lmls

目录也可以按照同样的方法改名。

【例 5】显示移动过程。如果我们想要知道在移动过程中到底有哪些文件进行了移动，则可以使用 "-v" 选项来查看详细的移动信息。例如：

[root@localhost ~]# touch test1.txt test2.txt test3.txt
#建立三个测试文件
[root@localhost ~]# mv -v *.txt /tmp
"test1.txt" -> "/tmp/test1.txt"
"test2.txt" -> "/tmp/test2.txt"
"test3.txt" -> "/tmp/test3.txt"
#加入"-v"选项，可以看到有哪些文件进行了移动