目录
1.初始化库并导入数据
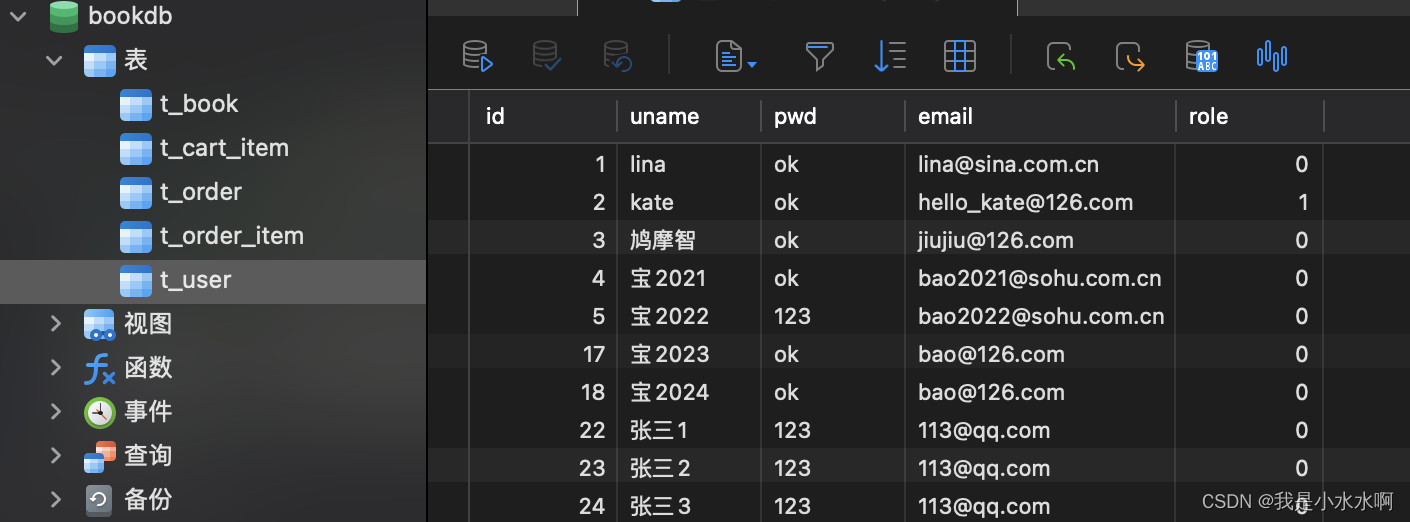
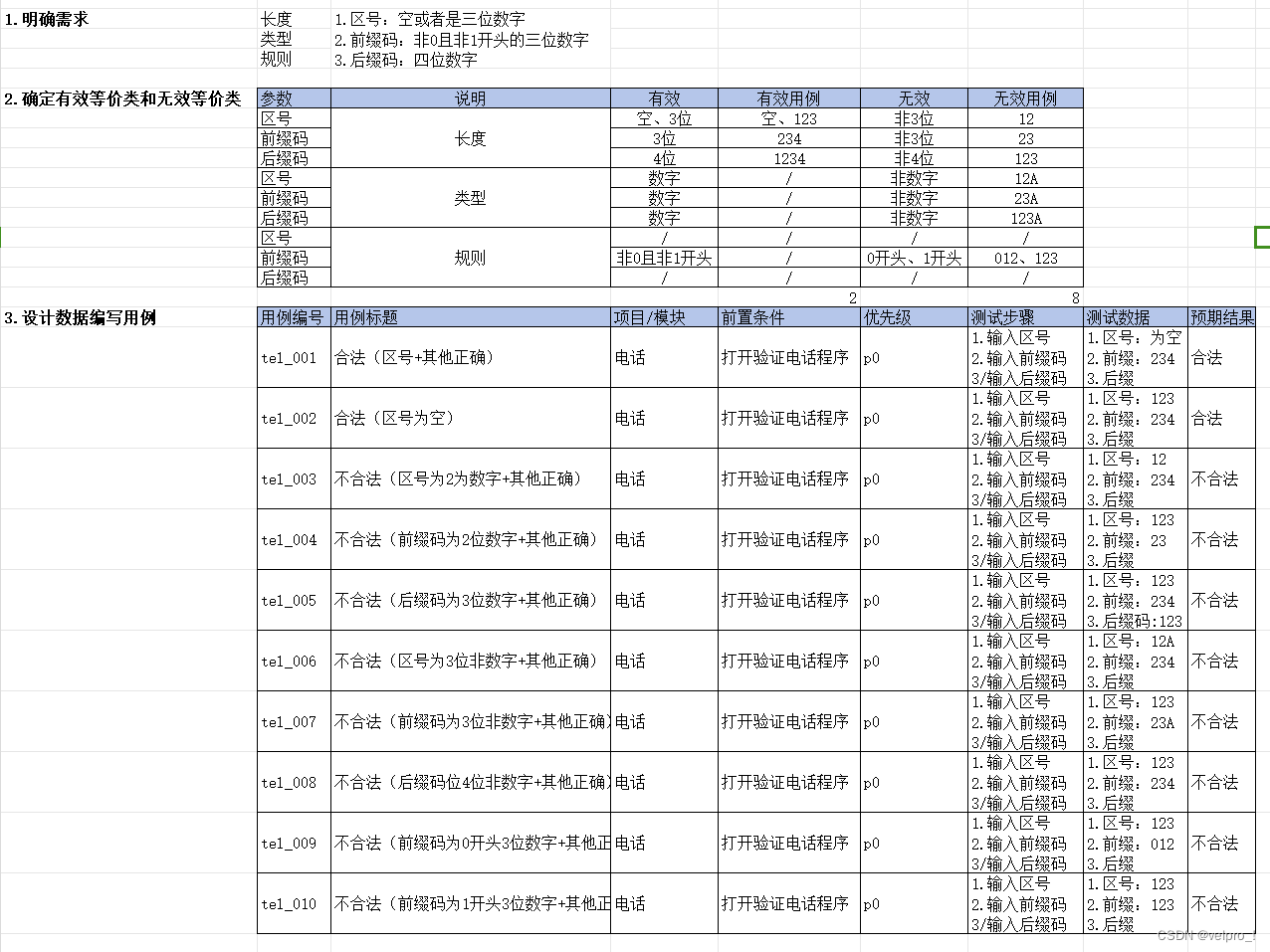
2.查看是否有缺失值,查看各个变量的相关性
3.探究各变量之间的相关关系
4.初始化并训练线性模型
5.可视化预测情况
6.模型优化
idea1:减少决策变量
idea2:数据归一化
idea3:尝试其他模型
XGB
Lasso 回归
Elasticnet
支持向量回归
决策树回归
1.初始化库并导入数据
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
plt.style.use('ggplot')
data = pd.read_csv('boston.csv')
data.head()2.查看是否有缺失值,查看各个变量的相关性
plt.figure(figsize=(12,8))
sns.heatmap(data.corr(),annot = True,fmt = '.2f',cmap='PuBu')
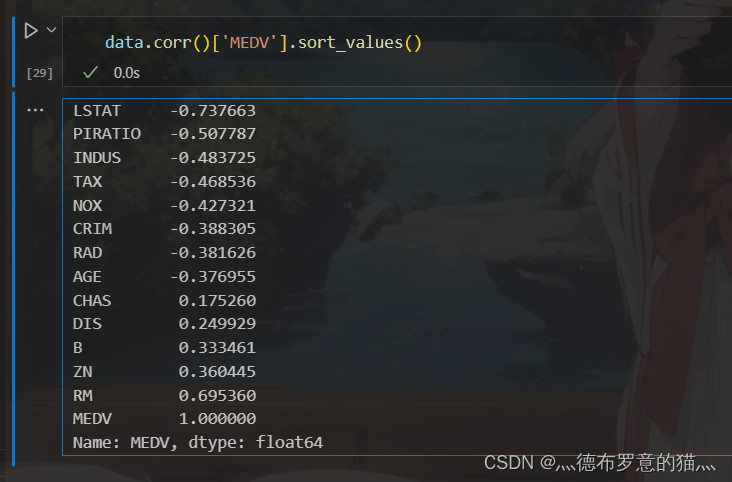
data.corr()['MEDV'].sort_values()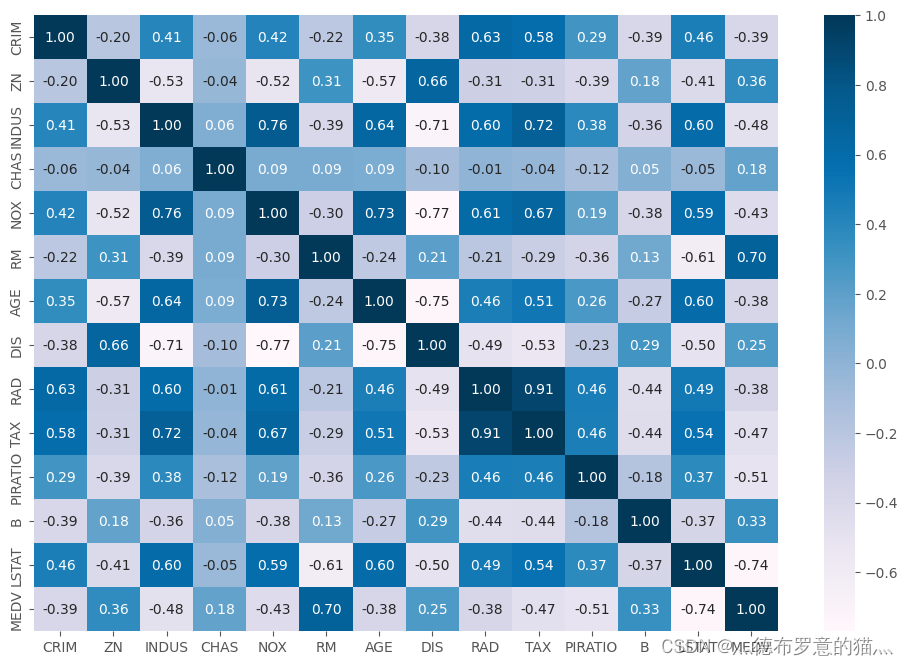
3.探究各变量之间的相关关系
sns.pairplot(data[["LSTAT","RM","PIRATIO","MEDV"]])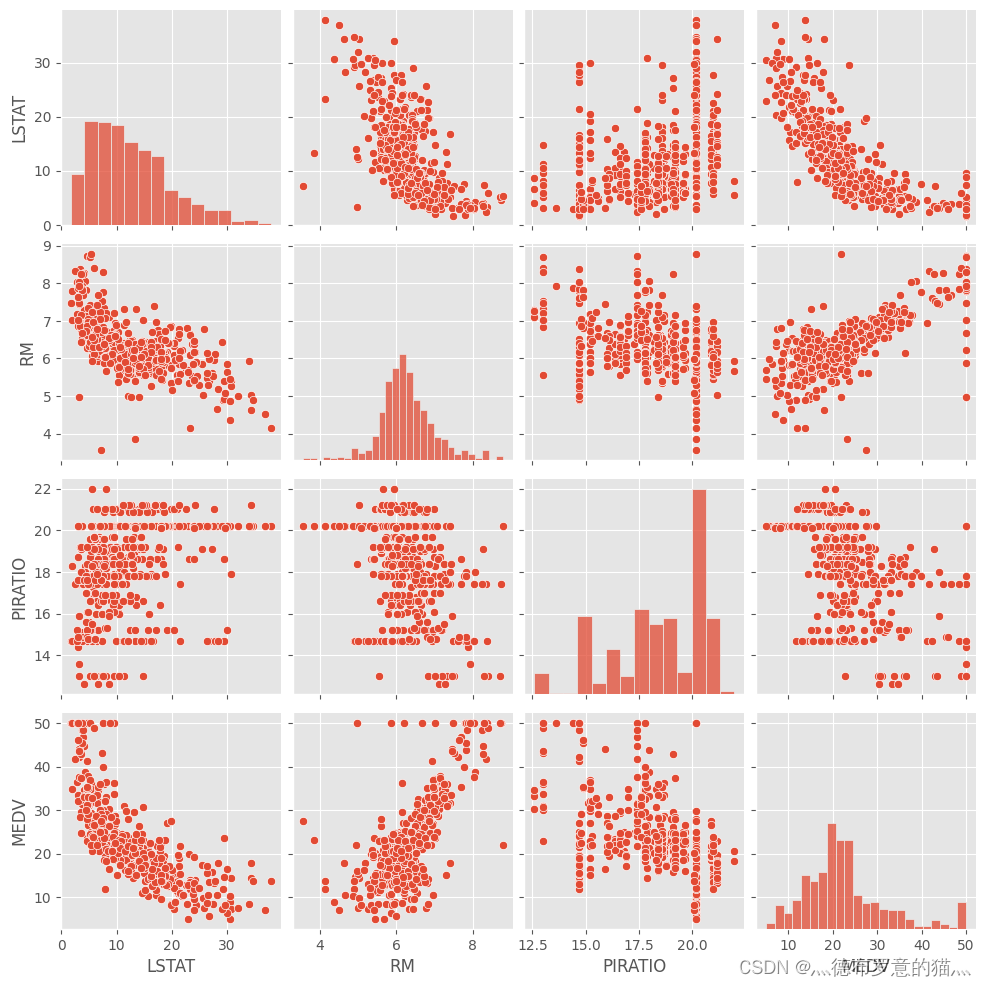
4.初始化并训练线性模型
X,y =data[data.columns.delete(-1)],data['MEDV']
xtarin,xtest,ytrain,ytest = train_test_split(X,y,test_size=0.2,random_state=750)
linear_model = LinearRegression()
linear_model.fit(xtarin,ytrain)
coef = linear_model.coef_
line_predict = linear_model.predict(xtest)
print('Score:{:.4f}'.format(linear_model.score(xtest,ytest)))
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(ytest,line_predict))))
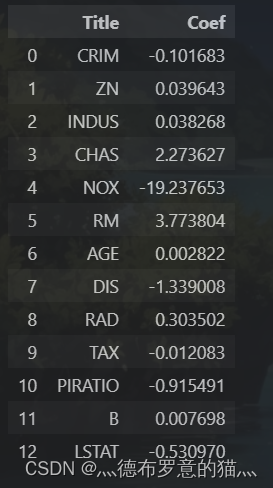
print(coef)
df_coef = pd.DataFrame()
df_coef['Title'] = data.columns.delete(-1)
df_coef['Coef'] = coef
df_coef并可视化各个变量的决策参数
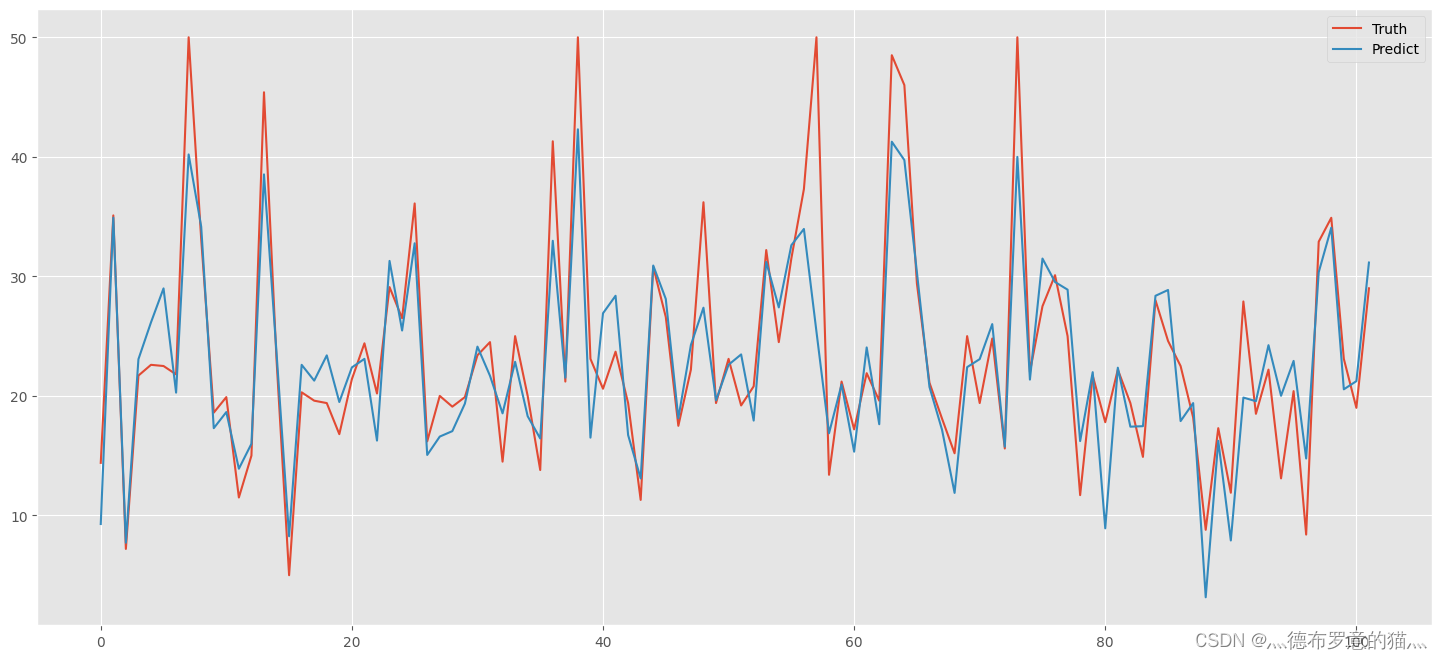
5.可视化预测情况
hos_predict = pd.DataFrame()
hos_predict['Truth'] =ytest
hos_predict['Predict'] = line_predict
hos_predict.reset_index(drop=True,inplace=True)
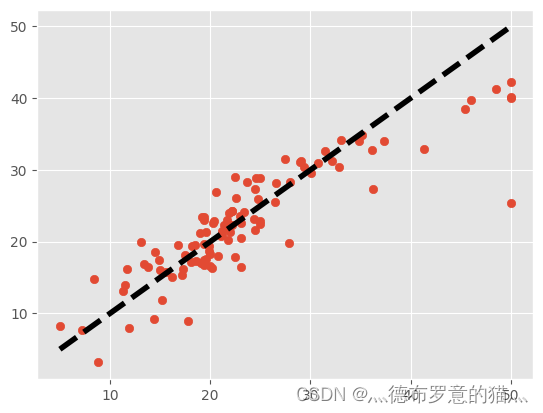
plt.scatter(ytest, line_predict,label='y')
plt.plot([ytest.min(), ytest.max()], [ytest.min(), ytest.max()], 'k--', lw=4,label='predicted')
6.模型优化
idea1:减少决策变量
取相关性最大的三个作为决策变量试试:
data.corr()['MEDV'].abs().sort_values(ascending=False).head(4)
x2 = np.array(data[['LSTAT','RM','PIRATIO']])
x2train,x2test,y2train,y2test = train_test_split(x2,y,random_state=750,test_size=0.2)
linear_model2 = LinearRegression()
linear_model2.fit(x2train,y2train)
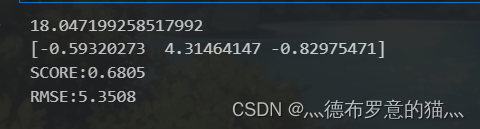
print(linear_model2.intercept_)
print(linear_model2.coef_)
line2_pre = linear_model2.predict(x2test) #预测值
print('SCORE:{:.4f}'.format(linear_model2.score(x2test, y2test)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y2test, line2_pre))))#RMSE(标准误差)
idea2:数据归一化
#归一化处理
from sklearn.preprocessing import StandardScaler
ss_x = StandardScaler()
x_train = ss_x.fit_transform(xtarin)
x_test = ss_x.transform(xtest)
ss_y = StandardScaler()
y_train = ss_y.fit_transform(ytrain.values.reshape(-1,1))
y_test = ss_y.transform(ytest.values.reshape(-1,1))
model3 = LinearRegression()
model3.fit(x_train,y_train)
print(model3.score(x_test,y_test))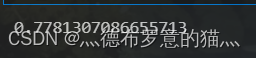
idea3:尝试其他模型
XGB
X ,y = data[data.columns.delete(-1)], data['MEDV']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=9)
from sklearn import ensemble
#params = {'n_estimators': 500, 'max_depth': 4, 'min_samples_split': 1,'learning_rate': 0.01, 'loss': 'ls'}
#clf = ensemble.GradientBoostingRegressor(**params)
clf = ensemble.GradientBoostingRegressor()
clf.fit(X_train, y_train)
clf_pre=clf.predict(X_test) #预测值
print('SCORE:{:.4f}'.format(clf.score(X_test, y_test)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test, clf_pre))))#RMSE(标准误差)

Lasso 回归
# Lasso 回归
from sklearn.linear_model import Lasso
lasso = Lasso()
lasso.fit(X_train,y_train)
y_predict_lasso = lasso.predict(X_test)
print('SCORE:{:.4f}'.format( lasso.score(X_test, y_test)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test,y_predict_lasso))))#RMSE(标准误差)

Elasticnet
from sklearn.linear_model import ElasticNet
enet = ElasticNet()
enet.fit(X_train,y_train)
y_predict_enet = enet.predict(X_test)
print('SCORE:{:.4f}'.format( enet.score(X_test, y_test)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test,y_predict_enet))))#RMSE(标准误差)
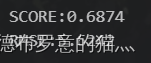
支持向量回归
from sklearn.preprocessing import StandardScaler
ss_x = StandardScaler()
X_train = ss_x.fit_transform(X_train)
X_test = ss_x.transform(X_test)
ss_y = StandardScaler()
y_train = ss_y.fit_transform(y_train.values.reshape(-1, 1))
y_test = ss_y.transform(y_test.values.reshape(-1, 1))
poly_svr = SVR(kernel="poly")
poly_svr.fit(X_train, y_train)
poly_svr_pre = poly_svr.predict(X_test)#预测值
print('SCORE:{:.4f}'.format(poly_svr.score(X_test, y_test)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test, poly_svr_pre))))#RMSE(标准误差)

决策树回归
from sklearn.tree import DecisionTreeRegressor
tree_reg=DecisionTreeRegressor(max_depth=2)
tree_reg.fit(X_train, y_train)
tree_reg_pre = tree_reg.predict(X_test)#预测值
print('SCORE:{:.4f}'.format( tree_reg.score(X_test, y_test)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test,tree_reg_pre))))#RMSE(标准误差)

参考:机器学习实战二:波士顿房价预测 Boston Housing_https://blog.csdn.net/weixin_45508265/article/deta_风信子的猫Redamancy的博客-CSDN博客