关键路径及关键路径算法[C/C++]

文章目录

- 关键路径
- - 引例
  - AOE网
  - 关键路径与关键活动
  - 关键路径算法
  - - 引例与原理
    - 关键路径算法的实现
    - - 边的存储结构
      - 代码实现
      - 运行示例

关键路径

关于拓扑排序的内容见拓扑排序详解

引例

通过拓扑排序我们可以解决一个工程是否可以顺序进行的问题，拓扑排序把一个工程分成了若干个流水级，只有当前流水级的工作完成才能进入下一个流水级，然而有时候我们还要解决工程完成的最短时间问题。比如说，造一辆汽车，我们要先造各种各样的零件、部件，最终再组装成车。外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

这些零部件都是在流水线上同时生产的，假如造一个轮子需要0.5天，造一个发动机需要3天，造一个车底盘需要2天，造一个外壳需要2天，造其他零部件需要2天，全部零部件集中到一处需要0.5天，组装成车需要2天，那么我们生产一辆车最短需要几天呢？

如果回答说把所有时间加起来，假如所有活动是串行的话，那么自然是每个活动时间相加，但是这些零件是分别在流水线上同时生产的，也就是说生产发动机的3天内我们可能已经生产了6个轮子，1.5个外壳，1.5个底盘了，而车的组装是在所有零部件都生产好之后才可以进行的，因此最短时间应该是先导活动中时间最长的发动机3天+集中零部件0.5天+组装车的2天，一共5.5天完成一辆车的生产。

因此，我们如果要对一个流程图求最短完成时间，就要分析它们的拓扑关系，并找到其中的关键流程，这个流程的时间就是最短时间。

AOE网

基于我们拓扑排序中AOV网(Activity On Vertex Network)，我们根据求流程的最短时间的需求，提出一个新的概念。在一个表示工程的带权有向图中，用顶点表示事件，用有向边表示活动，边上的权值表示活动的持续时间，这种有向图的边表示活动的网，我们称之为AOE网(Activity On Edge Network).

我们把AOE网中入度为0的点称为始点或源点，出度为0的点称为终点或汇点，它们分别代表工程的开始和结束，所以正常情况下，AOE网只有一个源点和一个汇点。如下图中，顶点vi代表一个事件，弧<vi , vj>则表示一个活动，其权值代表活动的持续时间。

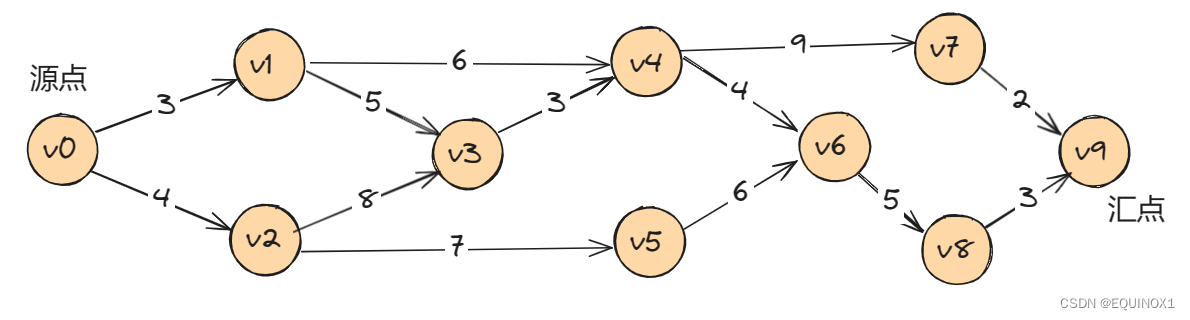
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

AOE网有着明显的工程特性，只有某顶点的事件发生后，由该顶点出发的各项活动才能开始。只有进入该顶点的所有活动都已经结束，该顶点的事件才能发生。

AOE网和AOV网有着相似之处，二者都是对工程进行建模，但又有很大差别。AOV网用顶点表示活动，它描述了活动间的偏序关系，AOE网则用边来表示活动，边上的权值表示活动的持续时间。仍以我们汽车的流水线生产为例，其AOV网和AOE网的对比体现了二者的差别。AOE网是建立在活动的偏序关系（或制约关系）没有矛盾的基础上，再来分析整个工程至少需要多少时间，以及为了缩短工程时间，可以加快哪些活动，或者对于各个活动ddl的限制等。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

关键路径与关键活动

我们把路径上各个活动所持续的时间之和称为路径长度，从源点到汇点具有最大长度的路径叫关键路径，在关键路径上的活动叫关键活动。显然就上图的AOE网而言，开始→发动机完成→部件集中到位→组装完成就是关键路径，路径长度为5.5。

我们发现，如果我们加快非关键路径上的活动，并不会缩短整个工程的时间，即使一个轮子只需要0.1的生产时间也无济于事，但是如果我们缩短了关键路径上关键活动的时间，如发动机缩短为2.5天，组装车缩短为1.5天，那么我们的关键路径长度就缩短为了4.5天。

所以我们如何去求关键路径呢？

关键路径算法

引例与原理

这是关于关键路径的一个很经典的例子。假设一个学生放学回家，除掉吃饭、洗漱外，到睡觉前有四小时空闲，而家庭作业需要两小时完成。不同的学生会有不同的做法，抓紧的学生，会在头两小时就完成作业，然后看看电视、读读课外书什么的;但也有超过一半的学生（比如我(悲)）会在最后两小时才去做作业，要不是因为没时间，可能还要再拖延下去。这也没什么好奇怪的，拖延就是人性几大弱点之一。

这里做家庭作业这一活动的最早开始时间是四小时的开始，可以理解为0，而最晚开始时间是两小时之后马上开始，不可以再晚，否则就是延迟了，此时可以理解为2。显然，当最早和最晚开始时间不相等时就意味着有空闲。接着，老妈发现了孩子拖延的小秘密（太痛了x_x），于是买了很多的课外习题，要求你四个小时，不许有一丝空闲，省得你拖延或偷懒。此时整个四小时全部被占满，最早开始时间和最晚开始时间都是0，因此它就是关键活动了。也就是说，我们只需要找到所有活动的最早开始时间和最晚开始时间，并且比较它们，如果相等就意味着此活动是关键活动，活动间的路径为关键路径。如果不等，则就不是。

关键路径算法的实现

那么关键路径的求解过程如下：

用数组etv(earliest time of vertex)和ltv(latest time of vertex)来存储事件的最早/最晚发生时间
$\left\{\begin{matrix} 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,当k=0时\\ max\left \{ etv[i]+len<vi,vk>\right \} .,当k≠0且 <vi,vk>∈p[k]时 \end{matrix}\right.$

其中p[ k ]为所有到达vk的边集合，转移方程保证了事件k在etv[ k ]发生时，其所有先导活动都能完成
$\left\{\begin{matrix} etv[k]\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,当k=n-1时\\ min\left \{ ltv[j]-len<vk,vj>\right \} ,当k≠n-1且 <vk,vj>∈S[k]时 \end{matrix}\right.$

其中S[k]为vk发出的边集合，转移方程保证了事件k在ltv[ k ]发生时，其发出的所有活动到达的事件都能在其最早开始时间完成
活动的最早开始时间即其先导事件的最早发生时间，因此只有先导事件发生了，活动才能开始
活动的最晚开始时间是其抵达事件的最晚发生时间减去活动时长，活动再晚也不能等其到达的事件发生了才开始，所以要赶在到达的事件发生之前

这里我们使用邻接表来存储边。

边的存储结构

vector<int> etv, ltv; // 事件最早发生时间
stack<int> path;      // 存储拓扑序列
struct Edge
{
    Edge(int a, int w) : adjvex(a), weight(w), _next(nullptr)
    {
    }
    // int in;//边的起点，这里省去
    int adjvex;//边的终点
    int weight;//权值
    Edge *_next;//in发出的下一条边
};

代码实现

求解etv的过程就是一次拓扑排序，只不过加了行对于elv的更新，开始事件的etv显然是0，由开始事件往后由拓扑顺序更新etv

而求解ltv其实就是对于拓扑排序的逆过程，因为结束事件的etv和ltv显然相同，那么对拓扑序列逆向遍历，更新ltv

再根据ltv，etv和lte，ete的关系求寻找我们的关键活动

void TopoLogicalSort(vector<Edge *> &edges)
{
    int n = edges.size();
    etv.resize(n);
    vector<int> ind(n); // 记录入度
    for (auto e : edges)
    {
        while (e)
        {
            ind[e->adjvex]++;
            e = e->_next;
        }
    }
    queue<int> q;
    for (int i = 0; i < n; i++)
        if (!ind[i])
            q.push(i);
    int f;
    while (!q.empty())
    {
        f = q.front();
        q.pop();
        path.push(f); // 存储拓扑序列
        Edge *e = edges[f];
        while (e)
        {
            if (!(--ind[e->adjvex]))
                q.push(e->adjvex);
            if (e->weight + etv[f] > etv[e->adjvex])
                // 如果事件f的etv + 活动e的时间晚于etv[adjvex]，则更新事件adjvex的etv，保证adjvex的etv时，事件adjvex的所有先导活动都已完成
                etv[e->adjvex] = e->weight + etv[f];
            e = e->_next;
        }
    }
}
void CriticalPath(vector<Edge *> &edges)
{
    Edge *e = nullptr;
    int ete, lte; // 活动的最早最晚发生时间
    int n = edges.size(), t;
    TopoLogicalSort(edges);
    ltv.resize(n);
    for (int i = 0; i < n; i++)
        ltv[i] = etv[n - 1]; // 初始化最晚发生时间
    while (!path.empty())
    {
        t = path.top();
        path.pop();
        e = edges[t];
        while (e)
        {
            if (etv[e->adjvex] - e->weight < ltv[t]) // 保证事件t如果在etv开始，发出的活动到达的事件都能在其各自etv完成
                ltv[t] = etv[e->adjvex] - e->weight;
            e = e->_next;
        }
    }
    for (int i = 0; i < n; i++)
    {
        e = edges[i];
        ete = etv[i]; // 事件的最早发生时间和其发出活动的最早发生时间一致

        while (e)
        {
            lte = ltv[e->adjvex] - e->weight;
            if (lte == ete)
            {
                printf("<v%d-v%d> length:%d\n", i, e->adjvex, e->weight);
                break;
            }
            e = e->_next;
        }
    }
}

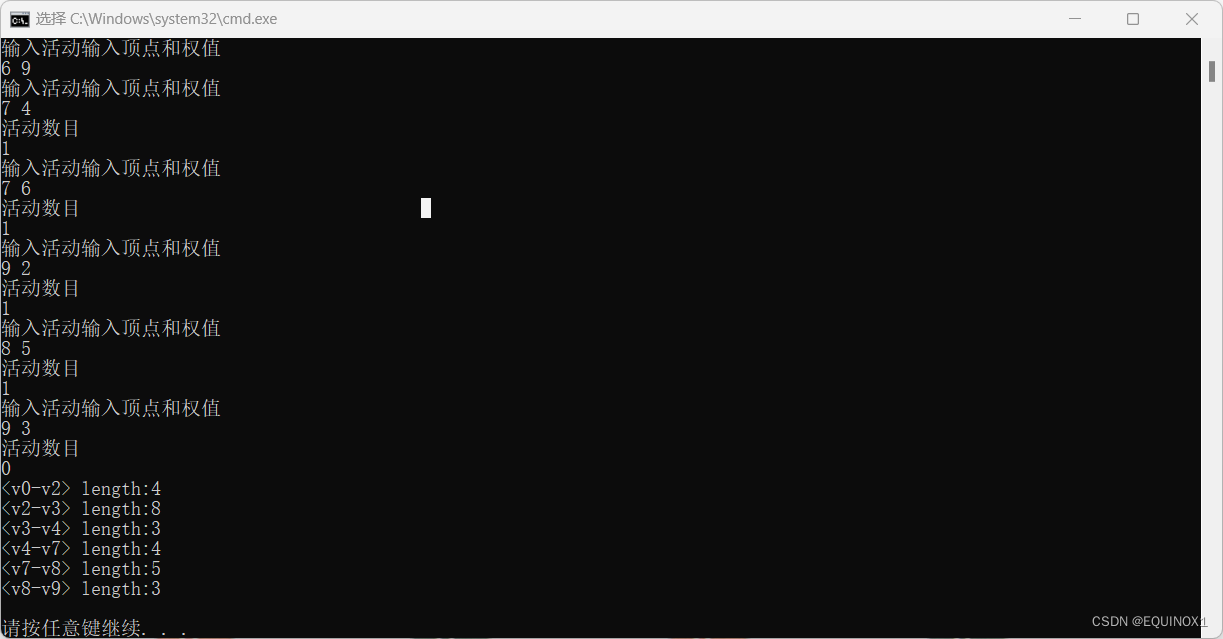
运行示例

运行代码

#include <iostream>
#include <vector>
#include <queue>
#include <stack>
using namespace std;
vector<int> etv, ltv; // 事件最早发生时间
stack<int> path;      // 存储拓扑序列
struct Edge
{
    Edge(int a, int w) : adjvex(a), weight(w), _next(nullptr)
    {
    }
    // int in;
    int adjvex;
    int weight;
    Edge *_next;
};
void TopoLogicalSort(vector<Edge *> &edges)
{
    int n = edges.size();
    etv.resize(n);
    vector<int> ind(n); // 记录入度
    for (auto e : edges)
    {
        while (e)
        {
            ind[e->adjvex]++;
            e = e->_next;
        }
    }
    queue<int> q;
    for (int i = 0; i < n; i++)
        if (!ind[i])
            q.push(i);
    int f;
    while (!q.empty())
    {
        f = q.front();
        q.pop();
        path.push(f); // 存储拓扑序列
        Edge *e = edges[f];
        while (e)
        {
            if (!(--ind[e->adjvex]))
                q.push(e->adjvex);
            if (e->weight + etv[f] > etv[e->adjvex])
                // 如果事件f的etv + 活动e的时间晚于etv[adjvex]，则更新事件adjvex的etv，保证adjvex的etv时，事件adjvex的所有先导活动都已完成
                etv[e->adjvex] = e->weight + etv[f];
            e = e->_next;
        }
    }
}
void CriticalPath(vector<Edge *> &edges)
{
    Edge *e = nullptr;
    int ete, lte; // 活动的最早最晚发生时间
    int n = edges.size(), t;
    TopoLogicalSort(edges);
    ltv.resize(n);
    for (int i = 0; i < n; i++)
        ltv[i] = etv[n - 1]; // 初始化最晚发生时间
    while (!path.empty())
    {
        t = path.top();
        path.pop();
        e = edges[t];
        while (e)
        {
            if (etv[e->adjvex] - e->weight < ltv[t]) // 保证事件t如果在etv开始，发出的活动到达的事件都能在其各自etv完成
                ltv[t] = etv[e->adjvex] - e->weight;
            e = e->_next;
        }
    }
    for (int i = 0; i < n; i++)
    {
        e = edges[i];
        ete = etv[i]; // 事件的最早发生时间和其发出活动的最早发生时间一致

        while (e)
        {
            lte = ltv[e->adjvex] - e->weight;
            if (lte == ete)
            {
                printf("<v%d-v%d> length:%d\n", i, e->adjvex, e->weight);
                break;
            }
            e = e->_next;
        }
    }
}
int main()
{
    int n, cnt, adj, w;
    cout << "请输入事件数量" << endl;
    cin >> n;
    Edge *e;
    vector<Edge *> edges(n, nullptr);
    for (int i = 0; i < n; i++)
    {
        cout << "活动数目" << endl;
        cin >> cnt;
        for (int j = 0; j < cnt; j++)
        {
            cout << "输入活动输入顶点和权值" << endl;
            cin >> adj >> w;
            e = new Edge(adj, w);
            e->_next = edges[i];
            edges[i] = e;
        }
    }
    CriticalPath(edges);
    return 0;
}

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传