写这篇文章的起因是14年有道题目:
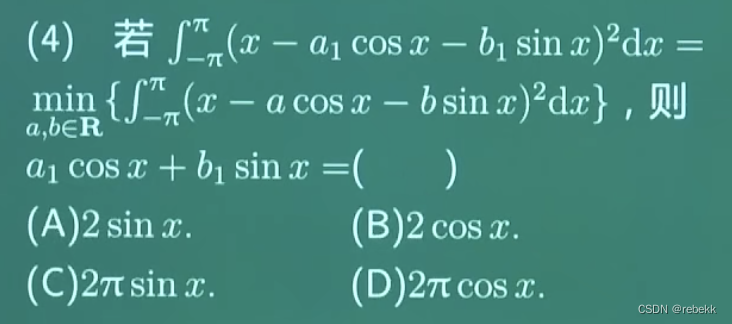
本题实质上是考察傅立叶级数的意义,因此要求扩大为不能只拘泥于傅里叶级数的计算相关问题,故作此篇。
一、课本上的内容
- 傅立叶级数:
设函数 f ( x ) f(x) f(x)是周期为 2 l 2l 2l的周期函数,且在 [ − l , l ] [-l,l] [−l,l]上可积,则称
a n = 1 l ∫ − l l f ( x ) c o s n π x l d x ( n = 0 , 1 , 2 , . . . ) a_n=\frac{1}{l}\int_{-l}^{l}f(x)cos\frac{n\pi x}{l}dx (n=0, 1, 2, ...) an=l1∫−llf(x)coslnπxdx(n=0,1,2,...)
b n = 1 l ∫ − l l f ( x ) s i n n π x l d x ( n = 0 , 1 , 2 , . . . ) b_n=\frac{1}{l}\int_{-l}^{l}f(x)sin\frac{n\pi x}{l}dx (n=0, 1, 2, ...) bn=l1∫−llf(x)sinlnπxdx(n=0,1,2,...)
为 f ( x ) f(x) f(x)的以 2 l 2l 2l为周期的傅立叶系数,称级数
a 0 2 + ∑ n = 1 ∞ ( a n c o s n π x l + b n s i n n π x l ) \frac{a_0}{2}+\sum_{n=1}^\infty (a_ncos\frac{n\pi x}{l}+b_nsin\frac{n\pi x}{l}) 2a0+n=1∑∞(ancoslnπx+bnsinlnπx)
为 f ( x ) f(x) f(x)的以 2 l 2l 2l为周期的傅立叶级数,记作
f ( x ) ∼ a 0 2 + ∑ n = 1 ∞ ( a n c o s n π x l + b n s i n n π x l ) f(x)\sim \frac{a_0}{2}+\sum_{n=1}^\infty (a_ncos\frac{n\pi x}{l}+b_nsin\frac{n\pi x}{l}) f(x)∼2a0+n=1∑∞(ancoslnπx+bnsinlnπx) - 狄利克雷收敛定理
设 f ( x ) f(x) f(x)是以 2 l 2l 2l为周期的可积函数,若在 [ − l , l ] [-l,l] [−l,l]上满足:1)连续或只有有限个第一类间断点;2)至多只有有限个极值点,
则 f ( x ) f(x) f(x)的傅立叶级数在 [ − l , l ] [-l,l] [−l,l]上处处收敛,记其和函数为 S ( x ) S(x) S(x),则
S ( x ) = { f ( x ) , x 为连续点, f ( x − 0 ) + f ( x + 0 ) 2 , x 为间断点, f ( − l + 0 ) + f ( l − 0 ) 2 , x = ± l . S(x)=\begin{cases}f(x),&x\text{ 为连续点,}\\[2ex]\dfrac{f(x-0)+f(x+0)}{2},&x\text{ 为间断点,}\\[2ex]\dfrac{f(-l+0)+f(l-0)}{2},&x=\pm l.\end{cases} S(x)=⎩ ⎨ ⎧f(x),2f(x−0)+f(x+0),2f(−l+0)+f(l−0),x 为连续点,x 为间断点,x=±l. - 正弦级数和余弦级数
f ( x ) ∼ a 0 2 + ∑ n = 1 ∞ ( a n c o s n π x l + b n s i n n π x l ) f(x)\sim \frac{a_0}{2}+\sum_{n=1}^\infty (a_ncos\frac{n\pi x}{l}+b_nsin\frac{n\pi x}{l}) f(x)∼2a0+n=1∑∞(ancoslnπx+bnsinlnπx)
{ a 0 = 1 l ∫ − l l f ( x ) d x a n = 1 l ∫ − l l f ( x ) cos n π x l d x , n = 1 , 2 , . . . b n = 1 l ∫ − l l f ( x ) sin n π x l d x , n = 1 , 2 , . . . \begin{cases}a_0=\frac{1}{l}\int_{-l}^lf(x)dx \\[2ex]a_n=\frac{1}{l}\int_{-l}^lf(x)\cos \dfrac{n\pi x}{l}dx,n=1,2,... \\[2ex]b_n=\frac{1}{l}\int_{-l}^lf(x)\sin \dfrac{n\pi x}{l}dx,n=1,2,... \end{cases} ⎩ ⎨ ⎧a0=l1∫−llf(x)dxan=l1∫−llf(x)coslnπxdx,n=1,2,...bn=l1∫−llf(x)sinlnπxdx,n=1,2,...- 当f(x)为奇函数时,其展开式是正弦级数
f ( x ) ∼ ∑ n = 1 ∞ b n s i n n π x l , b n = 2 l ∫ 0 l f ( x ) s i n n π x l d x , n = 1 , 2 , . . . f(x)\sim \sum_{n=1}^\infty b_nsin\frac{n\pi x}{l},b_n=\frac{2}{l}\int_0^lf(x)sin\frac{n\pi x}{l}dx,n=1, 2, ... f(x)∼n=1∑∞bnsinlnπx,bn=l2∫0lf(x)sinlnπxdx,n=1,2,... - 当f(x)为偶函数时,其展开式是余弦级数
f ( x ) ∼ a 0 2 + ∑ n = 1 ∞ a n cos n π x l f(x)\sim \frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos \frac{n\pi x}{l} f(x)∼2a0+n=1∑∞ancoslnπx
a 0 = 2 l ∫ 0 l f ( x ) d x , a n = 2 l ∫ 0 l f ( x ) cos n π x l d x , n = 1 , 2 , . . . a_0=\frac{2}{l}\int_{0}^lf(x)dx,a_n=\frac{2}{l}\int_0^lf(x)\cos \frac{n\pi x}{l}dx, n=1, 2, ... a0=l2∫0lf(x)dx,an=l2∫0lf(x)coslnπxdx,n=1,2,...
- 当f(x)为奇函数时,其展开式是正弦级数
二、傅立叶级数是怎么来的
一个函数可以由若干三角函数的和来逼近,即
f
(
x
)
≈
c
1
g
1
(
x
)
+
c
2
g
2
(
x
)
+
.
.
.
+
c
n
g
n
(
x
)
f(x)\approx c_1g_1(x)+c_2g_2(x)+...+c_ng_n(x)
f(x)≈c1g1(x)+c2g2(x)+...+cngn(x)
那么如何才能找到最合适的解,使得上式约等于符号左右两边最大限度地逼近呢?
做法是使二者的均方误差最小,即令下式最小:
ϵ
2
=
1
x
2
−
x
1
∫
x
1
x
2
[
f
(
x
)
−
∑
j
=
1
n
c
j
g
i
(
x
)
]
2
d
x
\epsilon^2=\frac{1}{x_2-x_1}\int_{x_1}^{x_2}[f(x)-\sum_{j=1}^nc_jg_i(x)]^2dx
ϵ2=x2−x11∫x1x2[f(x)−j=1∑ncjgi(x)]2dx
即令下式为零
∂
ϵ
2
∂
c
j
=
0
\frac{\partial \epsilon^2}{\partial c_{j}}=0
∂cj∂ϵ2=0
(这里详细的推导有空再写)
总之求导并使导数为零后,就能求出来傅立叶系数的值,因此也就有了最终的傅立叶级数的格式。
换句话来说,已知周期函数可用一系列三角函数之和来表示,这个和式就是傅立叶级数,而三角函数前面的系数就是傅立叶系数。傅立叶系数的选择,是为了使 I n = ∫ − π π [ f ( x ) − f n ( x ) ] 2 d x I_n=\int_{-\pi}^\pi [f(x)-f_n(x)]^2dx In=∫−ππ[f(x)−fn(x)]2dx达到最小
三、一些结论和回归本题
由上可知傅立叶级数的本质是用一系列三角函数去逼近一个周期函数。
了解这个之后,对于上面的题目,可以很轻松地看出等号右面的式子就是在算 f ( x ) = x f(x)=x f(x)=x和 g ( x ) = a c o s x + b s i n x g(x)=acosx+bsinx g(x)=acosx+bsinx这两个函数的逼近程度。取min值,就是在找最逼近的情况下,三角函数之前的系数是多少。
而由上可知,傅立叶级数的推导过程(实质上是傅立叶系数的推导过程),就是在令导数为零后求其系数值。也就是在求最逼近的一系列三角函数,其前面的系数是多少。
因此知这道题就是在求傅立叶系数。
再由项的数量和 cos n π x l = cos x \cos\frac{n\pi x}{l}=\cos x coslnπx=cosx可知让算的是n=1时的傅立叶系数(即正如题目中的名字一样,是傅立叶系数中的 a 1 a_1 a1和 b 1 b_1 b1)
由公式知
a
1
=
1
l
∫
−
l
l
f
(
x
)
cos
n
π
x
l
d
x
=
1
π
∫
−
π
π
x
cos
x
d
x
=
0
a_1=\frac{1}{l}\int_{-l}^{l}f(x)\cos \frac{n\pi x}{l}dx=\frac{1}{\pi}\int_{-\pi}^{\pi}x\cos xdx=0
a1=l1∫−llf(x)coslnπxdx=π1∫−ππxcosxdx=0
b
1
=
1
l
∫
−
l
l
f
(
x
)
sin
n
π
x
l
d
x
=
1
π
∫
−
π
π
x
sin
x
d
x
=
2
b_1=\frac{1}{l}\int_{-l}^{l}f(x)\sin \frac{n\pi x}{l}dx=\frac{1}{\pi}\int_{-\pi}^{\pi}x\sin xdx=2
b1=l1∫−llf(x)sinlnπxdx=π1∫−ππxsinxdx=2
所以得
a
1
cos
x
+
b
1
sin
x
=
2
sin
x
a_1\cos x+b_1\sin x=2\sin x
a1cosx+b1sinx=2sinx,故选A