数据结构——线性表①（顺序表）

一、线性表定义

线性表是一种数据结构，它是由n个具有相同数据类型的数据元素a1,a2,…,an组成的有限序列。

其中，除第一个元素a1外，每一个元素有且只有一个直接前驱元素，除了最后一个元素an外，每一个元素有且只有一个直接后继元素。

线性表可以用顺序存储结构或链式存储结构来实现。

顺序表是一种用一段地址连续的存储单元依次存储线性表中的数据元素的存储结构；
链表则是一种用一组任意的存储单元存储线性表中的数据元素的存储结构。

【线性表内容框架】
在这里插入图片描述

二、线性表特点

表中数据元素的个数有限
表中元素具有逻辑上的顺序性，表中元素有其先后次序
表中元素都是数据元素，每个元素都是单个元素
表中的元素数据类型都相同，即每个元素都占有相同大小的存储空间
表中元素具有抽象性，即仅讨论元素之间的逻辑关系，而不考虑元素究竟表示什么内容

三、线性表的基本操作

InitList(&L):初始化表。构造一个空的线性表L，分配内存空间。
DestroyList(&L):销毁操作。销毁线性表，并释放线性表L所占用的内存空间。
ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。
ListDelete(&L,i,&e):删除操作。删除表L中第i个位置的元素，并用e返回删除元素的值。
LocateElem(L,e):按值查找操作。在表L中查找具有给定关键字值的元素。
GetElem(L,i):按位查找操作。获取表L中第i个位置的元素的值。

【其他操作】

Length(L):求表长。返回线性表L的长度，即L中数据元素的个数
PrintList(L):输出操作。按前后顺序输出线性表L的所有元素值。
Empty(L):判空操作。若L为空表，则返回true，否则迟回false 。

注意：
上面写的函数严格来说并不正确，因为没有写返回值类型
其次，函数的参数有带符号“&”的，这是C++的语法，和C语言中的指针效果一致
比如说初始化表的函数，用C语言的写法，也可以写成 InitList(<类型名>* L);
要初始化一个数据元素类型为整型的线性表的话，初始化函数可以写成 InitList(int* L);

四、线性表的分类

（1）顺序表

1.1 顺序表的定义

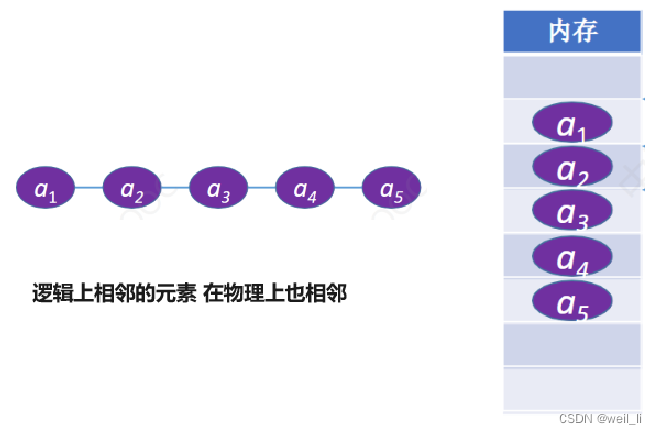
线性表的顺序存储叫做顺序表。（用顺序存储的方式实现线性表）

顺序存储——把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中，元素之间的关系由存储单元的邻接关系来体现。需要开辟一段了连续的空间用来存储数据。

在这里插入图片描述

1.2 顺序表的创建和初始化及相关操作

这里插一句，顺序表有两种，一种是动态顺序表，一种是静态顺序表。
·静态顺序表使用定长数组存储元素
·而动态顺序表可以动态开辟内存，可以动态改变数组长度

静态顺序表的创建和初始化比较简单，
在这里插入图片描述
静态顺序表的创建就是直接在main函数中创建一个SqList 类型的结构体变量
静态顺序表的初始化就是把链表结构体中的 length 的值设置为0

静态顺序表的基本操作：添加元素（插入元素）、删除元素、修改元素、查找元素

代码如下：

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>

#define MaxSize 10 //这里宏定义了静态顺序表最多能存储10个数据

struct SqList
{
	int data[MaxSize];
	int length;
};
typedef struct SqList SqList;

void InitList(SqList* list)//初始化静态顺序表
{
	list->length = 0;
}

int ListInsert(SqList* L, int i, int e)//在表中位置i处，插入数据e
{
    if (i < 1 || i > L->length + 1 || L->length >= MaxSize) {
        return 0;
    }
    for (int j = L->length; j >= i; j--) 
    {
        L->data[j] = L->data[j - 1];
    }
    L->data[i - 1] = e;
    L->length++;
    return 1;
}

int ListDelete(SqList* L, int i) //删除表中位序为i的数据元素
{
    if (i < 1 || i > L->length)
    {
        return 0;
    }
    for (int j = i; j < L->length; j++)
    {
        L->data[j - 1] = L->data[j];
    }
    L->length--;
    return 1;
}

void PrintList(SqList list)//打印顺序表中所有元素
{
    for (int i = 0; i < list.length; i++)
    {
        printf("%d ", list.data[i]);
    }
}

int Find(SqList list,int e)//查找顺序表中值为e 的元素，返回其位序，如果没找到，返回0
{
    if (list.length == 0)
    {
        return 0;
    }
    for (int i = 0; i < list.length; i++)
    {
        if (list.data[i] == e)
        {
            return i + 1;
        }
    }
    return 0;
}

int Change(SqList* list,int i,int e)//修改位序为i处的数据，把数据改成e
{
    if (i < 1 || i > list->length + 1 || list->length >= MaxSize) {
        return 0;
    }
    list->data[i-1] = e;
    return 1;
}

#include"SqList.h"

int main() 
{
    SqList L;
    InitList(&L);
    ListInsert(&L, 1, 10);//在位序1处插入数字10
    ListInsert(&L, 2, 20);//在位序2处插入数字20
    ListInsert(&L, 3, 30);//在位序3处插入数字30
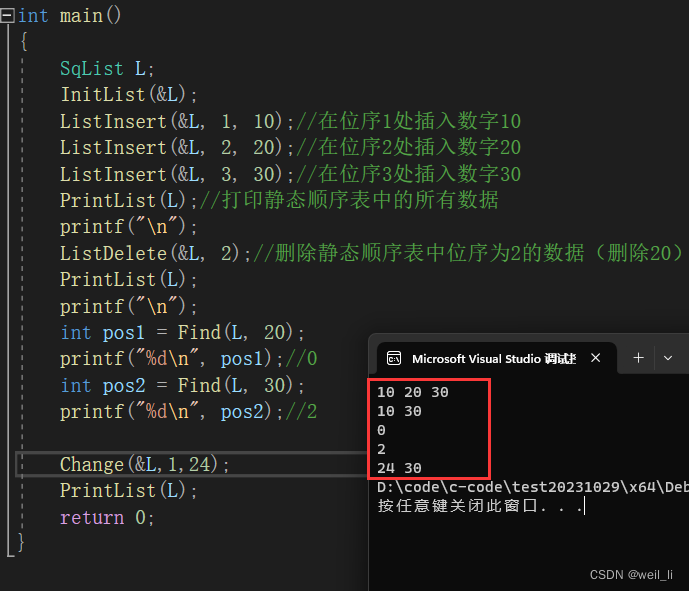
    PrintList(L);//打印静态顺序表中的所有数据
    printf("\n");
    ListDelete(&L, 2);//删除静态顺序表中位序为2的数据（删除20）
    PrintList(L);
    printf("\n");
    int pos1 = Find(L, 20);
    printf("%d\n", pos1);//0
    int pos2 = Find(L, 30);
    printf("%d\n", pos2);//2
    Change(&L,1,24);
    PrintList(L);//24 30
    return 0;
}

在这里插入图片描述

动态顺序表的创建和初始化

#define InitSize 10  //顺序表的初始长度
typedef struct
{
	ElemType *data; //指示动态分配数组的指针
	int MaxSize;    //顺序表的最大容量
	int length;     //顺序表的当前长度
}seqList;
//顺序表的类型定义（动态顺序表)

动态顺序表的好处是可以在容量不够的情况下进行扩容操作
动态顺序表的创建：在main函数中创建一个结构体变量
动态顺序表的初始化：用malloc开辟一段连续空间；初始化最大容量为宏定义的初始化长度；令顺序表的当前长度为0

动态顺序表的增删改查的函数操作实现

代码如下

#define InitSize 10  //顺序表的初始长度  
typedef int ElemType;
typedef struct seqList
{
	ElemType* data; //动态分配数组的指针  
	int MaxSize;    //顺序表的最大容量  
	int length;     //顺序表的当前长度  
} seqList;

void InitList(seqList* L)//动态顺序表的初始化
{
	L->data = (int*)malloc(InitSize * sizeof(int));//用malloc函数申请一片连续的存储空间
	L->length = 0;
	L->MaxSize = InitSize;
}

//增加动态数组的长度
void Increasesize(seqList* L, int len)
{
	int* p = L->data;
	L->data = (int*)malloc((L->MaxSize + len) * sizeof(int));
	for (int i = 0; i < L->length; i++)
	{
		L->data[i] = p[i];
	}
	L->MaxSize = L->MaxSize + len; 
	free(p);
}

// 插入元素  
int InsertList(seqList* L, int index, ElemType elem) {
    if (index < 0 || index > L->length || L->length == L->MaxSize) {
        return 0; // index error 或 溢出  
    }
    for (int i = L->length; i >= index; i--) {
        L->data[i + 1] = L->data[i]; // 后移一位  
    }
    L->data[index] = elem; // 插入新元素  
    L->length++; // 长度加一  
    return 1; // 插入成功  
}

// 删除元素  
int DeleteList(seqList* L, int index) {
    if (index < 0 || index >= L->length) {
        return 0; // index error  
    }
    for (int i = index; i < L->length - 1; i++) {
        L->data[i] = L->data[i + 1]; // 前移一位  
    }
    L->length--; // 长度减一  
    return 1; // 删除成功  
}

// 查找元素，返回元素位置，未找到返回-1  
int FindList(seqList* L, ElemType elem) {
    for (int i = 0; i < L->length; i++) {
        if (L->data[i] == elem) {
            return i; // 找到元素，返回位置  
        }
    }
    return -1; // 未找到元素，返回-1  
}

// 修改元素，返回修改结果，未找到返回-1  
int UpdateList(seqList* L, int index, ElemType elem) {
    if (index < 0 || index >= L->length) {
        return 0; // index error  
    }
    L->data[index] = elem; // 修改元素值  
    return 1; // 修改成功，返回1  
}