1.移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

// 题解：使用双指针，其中快指针指向非零元素，慢指针指向首个零元素下标
void moveZeroes(vector<int>& nums) {
	int slowIdx = 0;
	for (int fastIdx = 0; fastIdx < nums.size(); ++fastIdx) {
		if (nums[fastIdx] != 0) {
			std::swap(nums[slowIdx++], nums[fastIdx]);
		}
	}
}

2.盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。

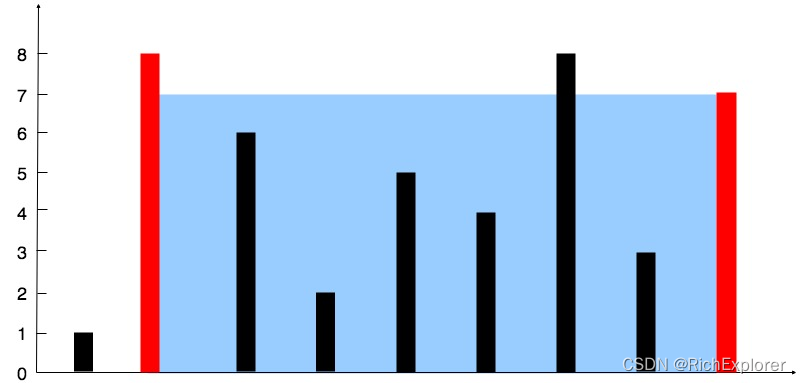
// 题解：面积公式 area = std::min(height[i], height[j]) * (j - i)
// 指针从两端向内部移动，当长板向内移动时，短板会变小或者不变，面积一定变小；当短板向内移动时，短板可能会变大，面积也有可能变大，因此只需要不断移动短板便可遍历得到最大面积；
int maxArea(vector<int>& height) {
	int left_idx = 0;
	int right_idx = height.size() - 1;
	int area = 0;
	while (left_idx < right_idx) {
		// 需要注意，下标是先使用后自增或者自减
		area = height[left_idx] < height[right_idx] ?
			std::max(area, (right_idx - left_idx) * height[left_idx++]) :
			std::max(area, (right_idx - left_idx) * height[right_idx--]);
	}
	return area;
}

3.三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

// 题解：双指针重复查询
// 排序数组，从前向后逐步遍历数据，按照双指针遍历内部数据，构建三元组形式，需要注意的是如何正确去重元素
vector<vector<int>> threeSum(vector<int>& nums) {
	if (nums.empty()) {
		return vector<vector<int>>();
	}
	std::sort(nums.begin(), nums.end());
	vector<vector<int>> results;
	for (int i = 0; i < nums.size(); ++i) {
		if (nums[i] > 0) {
			return results;
		}
		// 去除重复数据
		if (i > 0 && nums[i] == nums[i - 1]) continue;
		int left = 0;
		int right = nums.size() - 1;
		while (left < right) {
			int target = nums[left] + nums[right] + nums[i];
			if (target > 0) {
				right--;
			} else if (target < 0) {
				left++;
			} else {
				results.push_bakc({nums[i], nums[left], nums[right]});
				// 数组内部去除重复数据
				while (left < right && nums[left] == nums[left + 1]) left++;
				while (left < right && nums[right] == nums[right - 1]) right--;

				// 更新新的下标
				left--;
				right++;
			}
		}
	}
	return results;
}