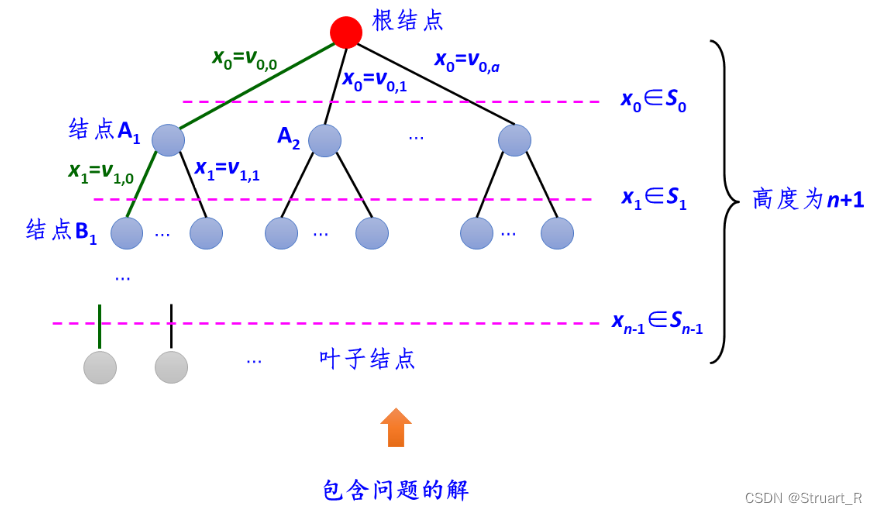
一、回溯法
回溯法采用DFS+剪枝的方式,通过剪枝删掉不满足条件的树,提高本身作为穷举搜索的效率。
回溯法一般有子集树和排列树两种方式,下面的装载问题和01背包问题属于子集树的范畴。
解空间类型:
子集树:所给的问题是从n个元素的集合S中找出满足某种性质的子集,例如装载问题、0-1背包问题。
排列树:所给的问题是确定n个元素满足某种性质的排列,例如旅行商问题。
回溯法所搜索的解结果,都在树的叶子结点上,一般左树为添加元素(1),右树为不添加元素(0)。
剪枝策略:
左剪枝:当前扩展节点,加入左枝后,不符合约束条件要求,那么就直接剪掉这个子节点及其所有子树,不再继续搜索。
右剪枝:当前扩展节点,加入右枝后,已经无法继续寻求最优解,后续子树也无法存在最优解,或者相比于之前遍历的叶子结点来说,更好的最优解,那么就剪掉这个子节点及其所有子树,不再继续搜索。
二、简单装载问题
1、算法设计
简单装载问题:n个集装箱装进一艘载重量为W的轮船,其中集装箱的重量为
,不考虑集装箱体积。设计一个算法,要求选择若干集装箱装进轮船,使得不超过载重量W,且给出可行解,和最优解的箱子装载方式。
算法:回溯法,子集树算法。
算法参数表:
num:选择的集装箱数
tw:选择的集装箱重量和
rw:剩余的集装箱重量和
op:表示是否选择该集装箱,op=1则选择,op=0则不选
x[ ]:最优解的op操作符选择,可以用来输出最优的集装箱装载方案
静态变量:
n:物品个数
w[ ]:各种物品的重量
W:轮船总重量限额
minnum:最优解集装箱存放个数
maxw:最优解的总重量
dfs策略:
(1)先判断是否为叶子结点,若是则判断该解是否为最优解,若是最优解则把op数组存入x数组。最优解条件:当前解集装箱存放个数是否小于最优解集装箱存放个数,且选择的集装箱和小于轮船限额
(2)若不是叶子结点则进行扩展操作。
(3)先进行左扩展,若tw+w[i]<=W,即加入这个物品后,总重量不大于轮船限额,则继续扩展,否则剪枝。
(4)再进行右扩展,若tw+rw-w[i]>=W,即不加入这个物品时,所选集装箱总重和未选集装箱总重的和仍然不小于轮船限额,则继续扩展,否则剪枝。
2、代码
//回溯法最优装载问题
public class bestload {
static int n=5;
static int minnum=9999;
static int W=10; //w为每个箱子重量
static int maxw=0; //存放最优解总重量
static int w[]={0,5,2,6,4,3};
public static void main(String []args)
{
int rw=0; //rw为剩余集装箱重量和
for(int num:w)
rw+=num;
int op[]=new int[w.length]; //存放一个箱子是否装载
int x[]=new int[w.length];
System.out.println("所有可行解:");
dfs(0,0,rw,op,1,x);
System.out.println("最少物品的解:");
for(int i=1;i<w.length;i++)
if(x[i]==1)
System.out.print(w[i]+" ");
}
public static void dfs(int num,int tw,int rw,int op[],int i,int x[])
{
if(i>n)
{
if(tw<=W&&num<minnum)
{
maxw=tw;
minnum=num;
for(int j=1;j<=n;j++)
x[j]=op[j];
}
for(int j=1;j<=n;j++)
if(op[j]==1)
System.out.print(w[j]+" ");
System.out.println(" ");
}
else
{
op[i]=1; //优先左分枝
if(tw+w[i]<=W) //左分枝条件
dfs(num+1,tw+w[i],rw-w[i],op,i+1,x);
op[i]=0;
if(tw+rw-w[i]>=W)
dfs(num,tw,rw-w[i],op,i+1,x);
}
}
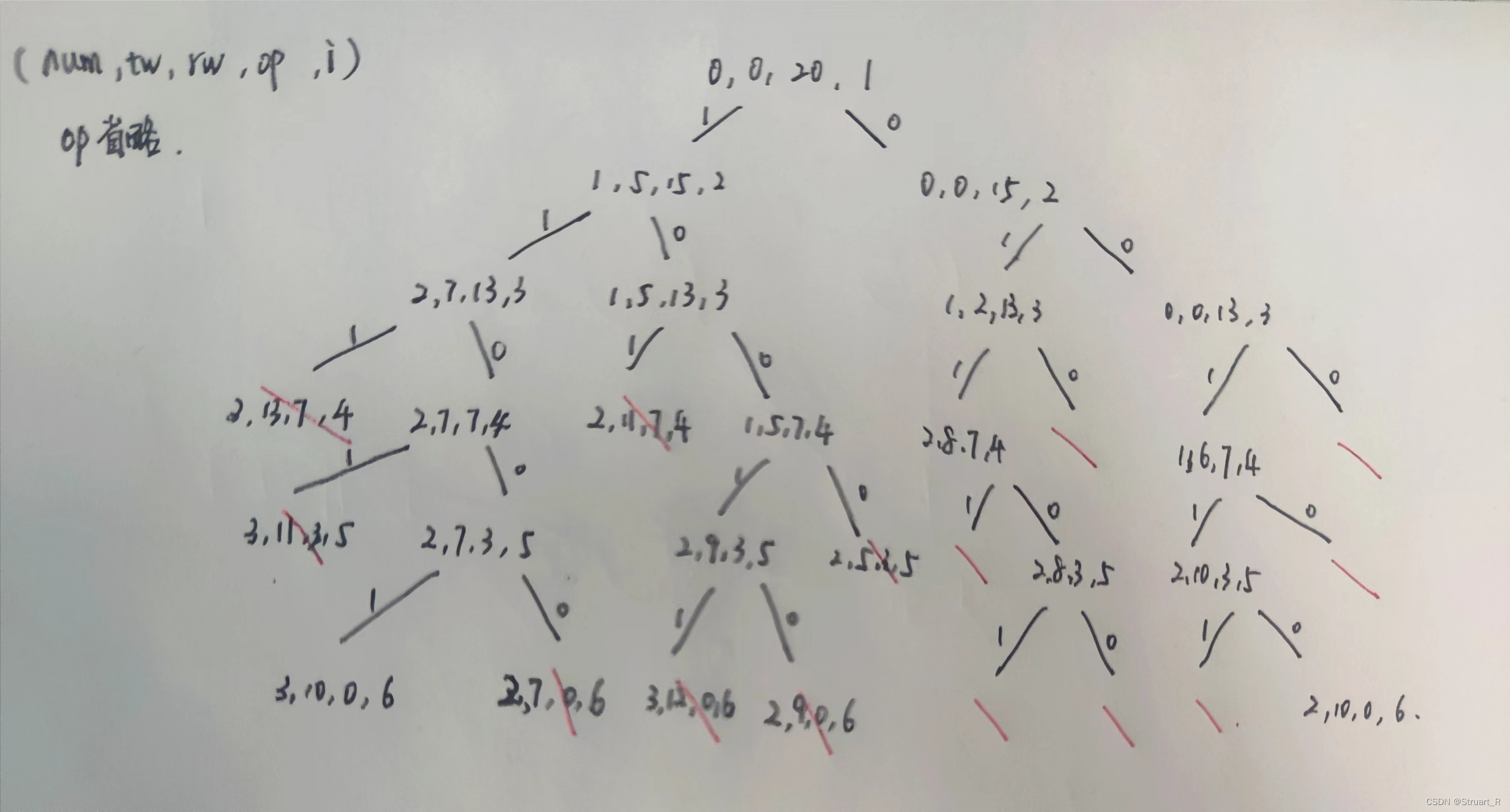
}子集树如下:(右树部分省略)
三、复杂装载问题
1、算法设计
复杂装载问题:n个集装箱要装进两艘载重量分别为c1和c2的轮船,其中集装箱的重量为
,不考虑集装箱体积,设计一个算法,使得这些集装箱装上这两艘轮船,如果不能装载则返回load false。
算法:回溯法,子集树算法,优先第一个轮船装载,判断第二个轮船是否能够装载剩余集装箱。
dfs策略:
(1)先判断是否为叶子结点,若是则判断该解是否为最优解,若是最优解则把op数组存入x数组。最优解条件:当前选择的集装箱和是否大于第一个轮船的最优集装箱装载重量,且选择的集装箱和小于第一个轮船限额
(2)若不是叶子结点则进行扩展操作。
(3)先进行左扩展,若tw+w[i]<=c1,即加入这个物品后,总重量不大于第一个轮船限额,则继续扩展,否则剪枝。
(4)再进行右扩展,若tw+rw-w[i]>=maxw,即不加入这个物品时,所选集装箱总重和未选集装箱总重的和仍然不小于第一个轮船的最优装载重量和,则继续扩展,否则剪枝。
2、代码
//回溯法复杂装载问题
public class complexbestload {
static int n=3;
static int minnum=9999;
static int c1=50; //w为每个箱子重量
static int c2=50;
static int maxw=0; //存放最优解总重量
static int w[]={0,10,40,40};
public static void main(String []args)
{
int rw=0; //rw为剩余集装箱重量和
for(int num:w)
rw+=num;
int op[]=new int[w.length]; //存放一个箱子是否装载
int x[]=new int[w.length];
dfs(0,0,rw,op,1,x);
judge(x);
}
public static void dfs(int num,int tw,int rw,int op[],int i,int x[])
{
if(i>n) //dfs搜索到最后一层,所有的货物都试了一遍,则输出最优解
{
if(tw<=c1&&tw>maxw)
{
maxw=tw;
for(int j=1;j<=n;j++)
x[j]=op[j];
}
}
else
{
op[i]=1; //优先左分枝
if(tw+w[i]<=c1) //左分枝条件
dfs(num+1,tw+w[i],rw-w[i],op,i+1,x);
op[i]=0;
if(tw+rw-w[i]>=maxw)
dfs(num,tw,rw-w[i],op,i+1,x);
}
}
public static void judge(int x[])
{
int total=0;
for(int i=1;i<w.length;i++)
if(x[i]==0)
total+=w[i];
if(total<=c2)
{
System.out.print("c1:");
for(int i=1;i<w.length;i++)
if(x[i]==1)
System.out.print(w[i]+" ");
System.out.println();
System.out.print("c2:");
for(int i=1;i<w.length;i++)
if(x[i]==0)
System.out.print(w[i]+" ");
}
else
System.out.println("load false");
}
}
四、0-1背包问题
1、算法设计
0-1背包问题:给定n个物品和一个背包,物品重量为,价值为
,背包容量为c,请设计一种算法,放入若干物品后,背包中物品总价值最大。
算法:回溯法,子集树算法。左剪枝结合贪心算法。
初始化:首先对w数组和v数组进行重新排序,按照a数组,即单位重量价值最高的优先。下面代码使用快速排序。
dfs策略:
(1)先判断是否为叶子结点,若是则判断该解是否为最优解,若是最优解则把op数组存入x数组,最优解maxv替换为当前所选物品的总重量。最优解条件:当前所选物品总重量不大于背包限额,且所选物品的价值大于当前最优解maxv。
(2)若不是叶子结点则进行扩展操作。
(3)先进行左扩展,计算左分枝后,使用贪心算法计算已选物品与若干剩余物品,在背包未超重情况下的最大价值。若greed>maxv该最大价值已经大于当前已知最优解maxv且tw+w[i]<=W当前已选物品的总重量加上新物品仍然不大于背包限额,则进行扩展,否则剪枝。
(4)再进行右扩展,若tw+rw-w[i]>=maxw,即不加入这个物品时,所选物品总重和剩余物品总重的和仍然不小于背包限额,则继续扩展,否则剪枝。
2、代码
//回溯法解决0-1背包问题
public class backage {
static int W=10;
static int maxv=0; //存放最优解价值
public static void main(String[] args)
{
double w[]={0,2,1,3,4,6};
double v[]={0,3,2,4,5,8};
int n=w.length-1;
double rw=0;
double a[]=new double[w.length];
int op[]=new int[w.length]; //存放当前叶子结点的解
int x[]=new int[w.length]; //存放最优解
for(int i=1;i<w.length;i++)
a[i]=v[i]/w[i];
for(int i=1;i<w.length;i++)
rw+=w[i];
//快排
quickSort(a, w, v, 1, n);
//回溯
dfs(w,v,0,0,rw,op,x,1);
int total=0;
for(int j=1;j<w.length;j++)
{
if(x[j]==1)
{
System.out.print(w[j]+" ");
total+=v[j];
}
}
System.out.println();
System.out.println("Max value:"+total);
}
//快速排序
public static void quickSort(double arr[],double w[],double v[],int low,int high)
{
int i=low;
int j=high;
int t;
if(low>high)
return;
double tmp=arr[low];
while(i<j)
{
while(i<j&&tmp>=arr[j]){j--;}; //注意由于降序排列,所以为tmp>=arr[j]
while(i<j&&tmp<=arr[i]){i++;}; //同理,tmp<=arr[i]
if(i<j)
{
swap(arr,i,j);
swap(w, i, j);
swap(v,i,j);
}
}
swap(arr,low,i);
swap(w,low,i);
swap(v,low,i);
quickSort(arr, w,v,low, j-1);
quickSort(arr,w,v,j+1,high);
}
//交换同一数组的两个值
public static void swap(double arr[],int i,int j)
{
double t;
t=arr[i];
arr[i]=arr[j];
arr[j]=t;
}
//回溯法
public static void dfs(double w[],double v[],int num,double tw, double rw, int op[],int x[],int i)
{
if(i>w.length-1)
{
if(tw<=W)
{
int tot=0;
for(int j=1;j<w.length;j++)
{
if(op[j]==1)
{
tot+=v[j];
}
}
if(tot>maxv)
{
for(int j=1;j<w.length;j++)
x[j]=op[j];
maxv=tot;
}
}
}
else
{
op[i]=1; //优先左分枝
double greed=greedy(op, v, w, i);
if(tw+w[i]<=W&&greed>maxv) //左分枝条件
dfs(w,v,num+1,tw+w[i],rw-w[i],op,x,i+1);
op[i]=0;
if(tw+rw-w[i]>=W)
dfs(w,v,num,tw,rw-w[i],op,x,i+1);
}
}
//左剪枝贪心计算
public static double greedy(int op[],double v[],double w[],int i)
{
double totv=0;
double totw=0;
for(int j=1;j<=i;j++)
{
if(op[j]==1)
{
totv+=v[j];
totw+=w[j];
}
}
for(int j=i+1;j<w.length;j++)
{
if(totw+w[j]<W)
{
totw+=w[j];
totv+=v[j];
}
else
{
totv+=(W-totw)*v[j]/w[j];
totw=W;
break;
}
}
return totv;
}
}

![git本地搭建服务器[Vmware虚拟机访问window的git服务器]](https://img-blog.csdnimg.cn/c8af2bfeece34633a743de37031cabaa.png)