一、递归简介
递归算法是一种直接或者间接调用自身函数或者方法的算法。
递归算法的实质是把问题分解成规模缩小的同类问题的子问题,然后递归调用方法来表示问题的解。递归算法对解决一大类问题很有效,它可以使算法简洁和易于理解。
递归本质是循环,循环推理。
递归是一种数学上分而自治的思想。
A、将原问题分解为规模较小的问题进行处理
分解后的问题与原问题类型完全相同,但规模较小。
通过小规模问题的解,能够轻易求得原生问题的解
B、问题的分解是有限的
当边界条件不能满足时,分解问题(继续递归)
当边界条件满足时,直接求解(递归结束)
二、递归在程序设计中的应用
递归函数:
函数体中存在自我调用的函数
递归函数必须有递归出口(边界条件)
函数的无限递归将导致程序崩溃
使用递归函数时不要陷入递归函数的执行细节,应首先建立递归模型和确立边界条件。
三、递归算法常见的应用场景
1.数据的定义是按递归定义的。如:斐波那契数列
2.问题解法按递归算法实现。如:递归求和
3.数据的结构形式是按递归定义的。如二叉树、广义表等
四、递归使用场景整理
1.树结构中使用递归
C#树结构操作逻辑整理
/// <summary>
/// 地区案例测试
/// </summary>
static void TestArea()
{
List<Area> list = new List<Area>() {
new Area(){ ID=1,Name="中国",ParentID=null},
new Area(){ ID=2,Name="山东",ParentID=1},
new Area(){ ID=3,Name="济南",ParentID=2},
new Area(){ ID=4,Name="槐荫",ParentID=3},
new Area(){ ID=5,Name="千乐微云",ParentID=4},
new Area(){ ID=6,Name="市中区",ParentID=3},
new Area(){ ID=7,Name="泉城广场",ParentID=6},
};
//转化为树结构展示
var result = getChild(null, list);
Console.WriteLine(result.ToJsonString());
}
/// <summary>
/// 递归处理子节点
/// </summary>
static List<Area> getChild(int? parentid, List<Area> source)
{
List<Area> result = new List<Area>();
//1.获取父节点
List<Area> parent = source.Where(q => q.ParentID == parentid).ToList();
if (parent.Count > 0)
{
//添加父类对象
result.AddRange(parent);
foreach (Area item in parent)
{
//循环父节点,获取子节点
item.Children = getChild(item.ID, source);
}
}
return result;
}
2.递归求和

/// <summary>
/// 递归求和
/// </summary>
static int Sum(int num)
{
if (num == 1)
return 1;
return num + Sum(num - 1);
}
//递归求和
Console.WriteLine(Sum(1));//1
Console.WriteLine(Sum(2));//3
Console.WriteLine(Sum(3));//6
Console.WriteLine(Sum(4));//103.递归计算阶乘
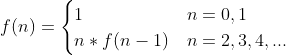
/// <summary>
/// 递归阶乘
/// </summary>
static int Factorial(int num)
{
if (num == 1)
return 1;
return num * Factorial(num - 1);
}
//递归阶乘
Console.WriteLine(Factorial(1));//1
Console.WriteLine(Factorial(2));//2
Console.WriteLine(Factorial(3));//6
Console.WriteLine(Factorial(4));//244.递归实现斐波那契数列
待完善.....
5.递归实现全排列
全排列算法(递归)封装
排列组合算法(递归)1
更多: