实验目的
1.理解感知机学习算法的基本思想:感知机是一种简单的线性分类模型,其基本思想是通过不断调整权重,使得分类超平面能够将不同类别的样本正确分开。
2.掌握感知机学习算法的实现方法:感知机学习算法基于随机梯度下降法,通过迭代更新权重,使得误分类点逐渐减少,最终达到收敛。
3.掌握感知机对偶算法的实现方法:感知机对偶算法通过引入拉格朗日乘子,将原始算法转化为对偶问题,从而避免了对每个样本都进行权重更新的过程,提高了算法的效率。
4.理解感知机算法的优缺点:感知机算法具有简单、易于理解、易于实现的优点,但也存在着收敛速度慢、对于线性不可分问题无法处理等缺点。
通过本实验,可以加深对感知机学习算法及其对偶算法的理解,为进一步学习和应用机器学习算法打下基础。
设备与环境
Jupyter notebook
python=3.9
三、实验原理
感知机算法的原理基于线性分类模型和随机梯度下降法,通过不断调整权重,使得分类超平面能够将不同类别的样本正确分开。感知机对偶算法通过引入拉格朗日乘子,将原始算法转化为对偶问题,从而避免了对每个样本都进行权重更新的过程,提高了算法的效率。
感知机学习算法的原始形式

感知机学习算法的对偶形式

实验内容
感知机算法的实现:编写Python代码实现感知机学习算法。感知机是一种二分类的线性分类器,其主要目标是找到一个超平面来将两类样本分开。算法的核心是通过迭代调整权重和偏置,使得误分类点逐渐减少直到收敛。
对偶算法的实现:编写Python代码实现感知机对偶算法。对偶算法是感知机的一种改进版本,它通过引入拉格朗日乘子来求解权重和偏置,避免了每次迭代都需要更新所有样本权重的问题。
实验结果分析
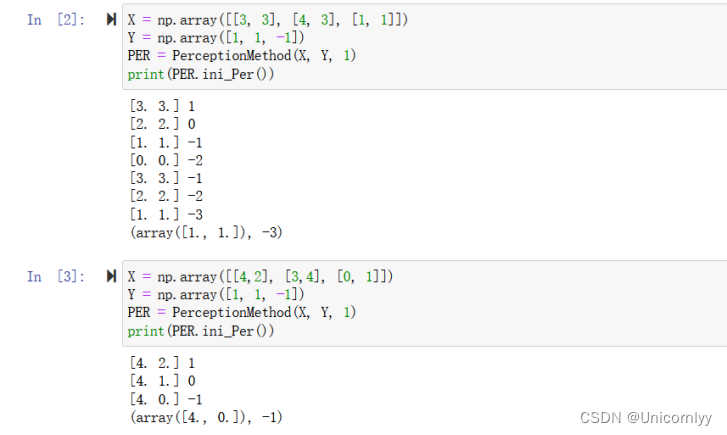
根据书上例子求解迭代过程表可以发现数据一模一样,说明该感知机学习算法没问题,其迭代过程是可靠的
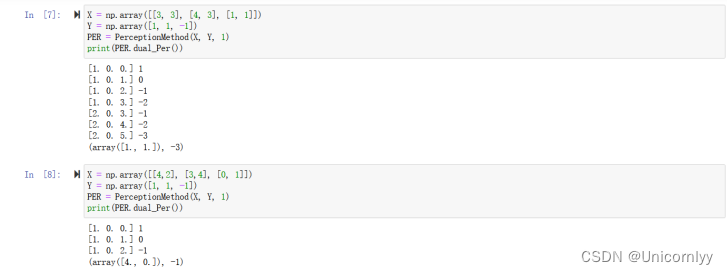
同理我们得到感知机对偶学习算法也是没有问题的
代码
感知机学习算法Python代码
import numpy as np
class PerceptionMethod(object): # 定义感知机学习类
def __init__(self, X, Y, eta): # 类中参数是 X,Y(X,Y)均为numpy数组,eta,eta是学习率
if X.shape[0] != Y.shape[0]: # 要求X,Y中的数目一样,即一个x对应一个y,否则返回错误
raise ValueError('Error,X and Y must be same when axis=0 ')
else: # 在类中储存参数
self.X = X
self.Y = Y
self.eta = eta
def ini_Per(self): # 感知机的原始形式
weight = np.zeros(self.X.shape[1]) # 初始化weight,b
b = 0
number = 0 # 记录训练次数
mistake = True # mistake是变量用来说明分类是否有错误
while mistake is True: # 当有错时
mistake = False # 开始下一轮纠错前需要将mistake变为true,一来判断这一轮是否有错误
for index in range(self.X.shape[0]): # 循环开始
if self.Y[index] * (weight @ self.X[index] + b) <= 0: # 错误判断条件
weight += self.eta * self.Y[index] * self.X[index] # 进行更新weight,b
b += self.eta * self.Y[index]
number += 1
print(weight, b)
mistake = True # 此轮检查出错误,表明mistake为true,进行下列一轮
break # 找出第一个错误后跳出循环
return weight, b # 返回值
X = np.array([[3, 3], [4, 3], [1, 1]])
Y = np.array([1, 1, -1])
PER = PerceptionMethod(X, Y, 1) #实例化了一个PerceptionMethod类的对象PER,并将X、Y和学习率(这里设为1)作为参数传递给该对象
print(PER.ini_Per())
X = np.array([[4,2], [3,4], [0, 1]])
Y = np.array([1, 1, -1])
PER = PerceptionMethod(X, Y, 1)
print(PER.ini_Per())
感知机对偶学习算法Python代码:
import numpy as np
class PerceptionMethod(obcject): # 定义感知机学习类
def __init__(self, X, Y, eta): # 类中参数是 X,Y(X,Y)均为numpy数组,eta,eta是学习率
if X.shape[0] != Y.shape[0]: # 要求X,Y中的数目一样,即一个x对应一个y,否则返回错误
raise ValueError('Error,X and Y must be same when axis=0 ')
else: # 在类中储存参数
self.X = X
self.Y = Y
self.eta = eta
def dual_Per(self): #感知机的对偶形式
Gram = np.dot(self.X, self.X.T) #定义Gram矩阵
alpha = np.zeros(self.X.shape[0]) #初始化alpha,b
b = 0
mistake = True # mistake是变量用来说明分类是否有错误
while mistake is True: #当有错时
mistake = False #开始下一轮纠错前需要将mistake变为true,一来判断这一轮是否有错误
for index in range(self.X.shape[0]): #循环开始
if self.Y[index] * (alpha * self.Y @ Gram[index] + b) <= 0: #错误判断条件
alpha[index] += self.eta 进行更新alpha,b
b += self.eta * self.Y[index]
print(alpha, b)
mistake = True #此轮检查出错误,表明mistake为true,进行下列一轮
break #找出第一个错误后跳出循环
weight = self.Y * alpha @ self.X #计算得到权重向量weight
return weight, b # 返回权重向量和偏置项
X = np.array([[3, 3], [4, 3], [1, 1]])
Y = np.array([1, 1, -1])
PER = PerceptionMethod(X, Y, 1)
print(PER.dual_Per())
X = np.array([[4,2], [3,4], [0, 1]])
Y = np.array([1, 1, -1])
PER = PerceptionMethod(X, Y, 1)
print(PER.dual_Per())