文章目录
- (一) 分布式理论算法和协议
- 1)CAP理论
- 总结
- 2)BASE理论
- BASE 理论的核心思想
- 基本可用
- 软状态
- 最终一致性
- 3)Paxos算法
- Basic Paxos 算法
- 4) Raft算法
- 1 拜占庭将军
- 5)Gossip协议
- (二) 分布式锁
- 分布式锁应该具备哪些条件
- 基于 redis 做分布式锁
- (三) 分布式事务
- 强一致性
- 弱一致性
- 最终一致性
- 柔性事务
- 幂等操作
- 分布式事务使用场景
- 转账
- 下单扣库存
- 同步超时
- 分布式事务的解决方案
- 1)两阶段提交/XA
- 本地消息表
- 可靠消息最终一致性
(一) 分布式理论算法和协议
1)CAP理论
CAP 理论/定理。起源于 2000 年,由加州大学伯克利分校的 Eric Brewer 教授在分布式计算原理研讨会(PODC)上提出,因此 CAP 定理又被称作 布鲁尔定理(Brewer’s theorem)
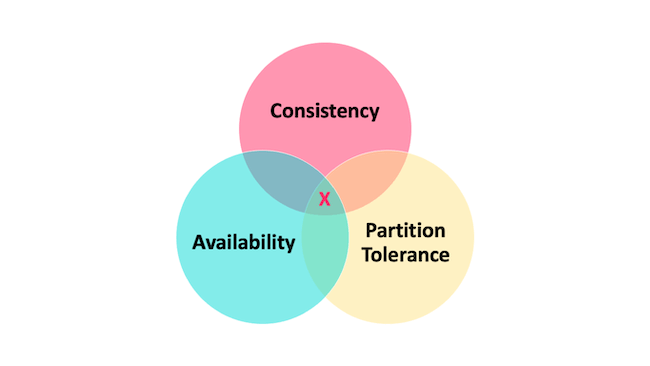
CAP 也就是 Consistency(一致性)、Availability(可用性)、Partition Tolerance(分区容错性) 这三个单词首字母组合。
在理论计算机科学中,CAP 定理(CAP theorem)指出对于一个分布式系统来说,当设计读写操作时,只能同时满足以下三点中的两个:
- 一致性(Consistency) : 所有节点访问同一份最新的数据副本
- 可用性(Availability): 非故障的节点在合理的时间内返回合理的响应(不是错误或者超时的响应)。
- 分区容错性(Partition Tolerance) : 分布式系统出现网络分区的时候,仍然能够对外提供服务。
当发生网络分区的时候,如果我们要继续服务,那么强一致性和可用性只能 2 选 1。也就是说当网络分区之后 P 是前提,决定了 P 之后才有 C 和 A 的选择。也就是说分区容错性(Partition tolerance)我们是必须要实现的。
简而言之就是:CAP 理论中分区容错性 P 是一定要满足的,在此基础上,只能满足可用性 A 或者一致性 C。
分布式系统理论上不可能选择 CA 架构,只能选择 CP 或者 AP 架构。 比如 ZooKeeper、HBase 就是 CP 架构,Cassandra、Eureka 就是 AP 架构,Nacos 不仅支持 CP 架构也支持 AP 架构。
常见的可以作为注册中心的组件有:ZooKeeper、Eureka、Nacos…。
- ZooKeeper 保证的是 CP。 任何时刻对 ZooKeeper 的读请求都能得到一致性的结果,但是, ZooKeeper 不保证每次请求的可用性比如在 Leader 选举过程中或者半数以上的机器不可用的时候服务就是不可用的。
- Eureka 保证的则是 AP。 Eureka 在设计的时候就是优先保证 A (可用性)。在 Eureka 中不存在什么 Leader 节点,每个节点都是一样的、平等的。因此 Eureka 不会像 ZooKeeper 那样出现选举过程中或者半数以上的机器不可用的时候服务就是不可用的情况。 Eureka 保证即使大部分节点挂掉也不会影响正常提供服务,只要有一个节点是可用的就行了。只不过这个节点上的数据可能并不是最新的。
- Nacos 不仅支持 CP 也支持 AP。
总结
在进行分布式系统设计和开发时,我们不应该仅仅局限在 CAP 问题上,还要关注系统的扩展性、可用性等等
在系统发生“分区”的情况下,CAP 理论只能满足 CP 或者 AP。要注意的是,这里的前提是系统发生了“分区”
如果系统没有发生“分区”的话,节点间的网络连接通信正常的话,也就不存在 P 了。这个时候,我们就可以同时保证 C 和 A 了。
总结:如果系统发生“分区”,我们要考虑选择 CP 还是 AP。如果系统没有发生“分区”的话,我们要思考如何保证 CA 。
2)BASE理论
BASE 是 Basically Available(基本可用)、Soft-state(软状态) 和 Eventually Consistent(最终一致性) 三个短语的缩写。BASE 理论是对 CAP 中一致性 C 和可用性 A 权衡的结果,其来源于对大规模互联网系统分布式实践的总结,是基于 CAP 定理逐步演化而来的,它大大降低了我们对系统的要求。
BASE 理论的核心思想
即使无法做到强一致性,但每个应用都可以根据自身业务特点,采用适当的方式来使系统达到最终一致性。
也就是牺牲数据的一致性来满足系统的高可用性,系统中一部分数据不可用或者不一致时,仍需要保持系统整体“主要可用”。
BASE 理论本质上是对 CAP 的延伸和补充,更具体地说,是对 CAP 中 AP 方案的一个补充。

基本可用
基本可用是指分布式系统在出现不可预知故障的时候,允许损失部分可用性。但是,这绝不等价于系统不可用。
什么叫允许损失部分可用性呢?
- 响应时间上的损失: 正常情况下,处理用户请求需要 0.5s 返回结果,但是由于系统出现故障,处理用户请求的时间变为 3 s。
- 系统功能上的损失:正常情况下,用户可以使用系统的全部功能,但是由于系统访问量突然剧增,系统的部分非核心功能无法使用。
软状态
软状态指允许系统中的数据存在中间状态(CAP 理论中的数据不一致),并认为该中间状态的存在不会影响系统的整体可用性,即允许系统在不同节点的数据副本之间进行数据同步的过程存在延时。
最终一致性
最终一致性强调的是系统中所有的数据副本,在经过一段时间的同步后,最终能够达到一个一致的状态。因此,最终一致性的本质是需要系统保证最终数据能够达到一致,而不需要实时保证系统数据的强一致性。
分布式一致性的 3 种级别:
强一致性:系统写入了什么,读出来的就是什么。
弱一致性:不一定可以读取到最新写入的值,也不保证多少时间之后读取到的数据是最新的,只是会尽量保证某个时刻达到数据一致的状态。
最终一致性:弱一致性的升级版,系统会保证在一定时间内达到数据一致的状态。
业界比较推崇是最终一致性级别,但是某些对数据一致要求十分严格的场景比如银行转账还是要保证强一致性。
3)Paxos算法
Paxos 算法是 Leslie Lamport在 1990 年提出了一种分布式系统 共识 算法。这也是第一个被证明完备的共识算法。
Paxos 算法是第一个被证明完备的分布式系统共识算法。共识算法的作用是让分布式系统中的多个节点之间对某个提案(Proposal)达成一致的看法。提案的含义在分布式系统中十分宽泛,像哪一个节点是 Leader 节点、多个事件发生的顺序等等都可以是一个提案。
Paxos 算法主要包含 2 个部分:
- Basic Paxos 算法:描述的是多节点之间如何就某个值(提案 Value)达成共识。
- Multi-Paxos 思想:描述的是执行多个 Basic Paxos 实例,就一系列值达成共识。Multi-Paxos 说白了就是执行多次 Basic Paxos ,核心还是 Basic Paxos 。
对 Paxos 算法的定义做一个总结:
- Paxos 算法是兰伯特在 1990 年提出了一种分布式系统共识算法。
- 兰伯特当时提出的 Paxos 算法主要包含 2 个部分: Basic Paxos 算法和 Multi-Paxos 思想。
- Raft 算法、ZAB 协议、 Fast Paxos 算法都是基于 Paxos 算法改进而来
Basic Paxos 算法
Basic Paxos 中存在 3 个重要的角色:
- 提议者(Proposer):也可以叫做协调者(coordinator),提议者负责接受客户端的请求并发起提案。提案信息通常包括提案编号 (Proposal ID) 和提议的值 (Value)。
- 接受者(Acceptor):也可以叫做投票员(voter),负责对提议者的提案进行投票,同时需要记住自己的投票历史;
- 学习者(Learner):如果有超过半数接受者就某个提议达成了共识,那么学习者就需要接受这个提议,并就该提议作出运算,然后将运算结果返回给客户端。
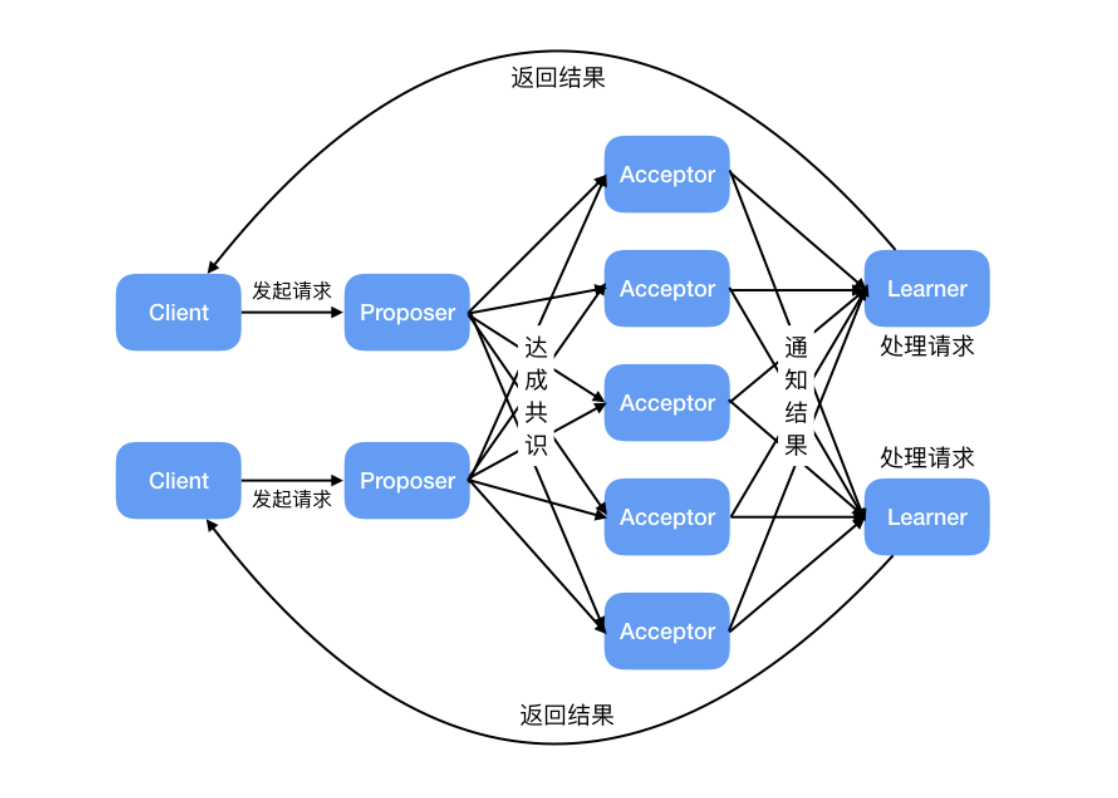
为了减少实现该算法所需的节点数,一个节点可以身兼多个角色。并且,一个提案被选定需要被半数以上的 Acceptor 接受。这样的话,Basic Paxos 算法还具备容错性,在少于一半的节点出现故障时,集群仍能正常工作。
4) Raft算法
Raft 是 Multi-Paxos 的一个变种,其简化了 Multi-Paxos 的思想,变得更容易被理解以及工程实现。
针对没有恶意节点的情况,除了 Raft 算法之外,当前最常用的一些共识算法比如 ZAB 协议、 Fast Paxos 算法都是基于 Paxos 算法改进的。
针对存在恶意节点的情况,一般使用的是 工作量证明(POW,Proof-of-Work)、 权益证明(PoS,Proof-of-Stake ) 等共识算法。这类共识算法最典型的应用就是区块链,就比如说前段时间以太坊官方宣布其共识机制正在从工作量证明(PoW)转变为权益证明(PoS)。
1 拜占庭将军
假设多位拜占庭将军中没有叛军,信使的信息可靠但有可能被暗杀的情况下,将军们如何达成是否要进攻的一致性决定?
解决方案大致可以理解成:先在所有的将军中选出一个大将军,用来做出所有的决定。
举例如下:假如现在一共有 3 个将军 A,B 和 C,每个将军都有一个随机时间的倒计时器,倒计时一结束,这个将军就把自己当成大将军候选人,然后派信使传递选举投票的信息给将军 B 和 C,如果将军 B 和 C 还没有把自己当作候选人(自己的倒计时还没有结束),并且没有把选举票投给其他人,它们就会把票投给将军 A,信使回到将军 A 时,将军 A 知道自己收到了足够的票数,成为大将军。在有了大将军之后,是否需要进攻就由大将军 A 决定,然后再去派信使通知另外两个将军,自己已经成为了大将军。如果一段时间还没收到将军 B 和 C 的回复(信使可能会被暗杀),那就再重派一个信使,直到收到回复。
5)Gossip协议
Gossip 直译过来就是闲话、流言蜚语的意思。流言蜚语有什么特点呢?容易被传播且传播速度还快,你传我我传他,然后大家都知道了。
Gossip 协议 也叫 Epidemic 协议(流行病协议)或者 Epidemic propagation 算法(疫情传播算法),别名很多。不过,这些名字的特点都具有 随机传播特性 (联想一下病毒传播、癌细胞扩散等生活中常见的情景),这也正是 Gossip 协议最主要的特点。
Gossip 协议是一种允许在分布式系统中共享状态的去中心化通信协议,通过这种通信协议,我们可以将信息传播给网络或集群中的所有成员。
(二) 分布式锁
对于单机多线程来说,在 Java 中,我们通常使用 ReetrantLock 类、synchronized 关键字这类 JDK 自带的 本地锁 来控制一个 JVM 进程内的多个线程对本地共享资源的访问。
- 当在分布式模型下,数据只有一份(或有限制),此时需要利用锁的技术控制某一时刻修改数据的进程数。
- 与单机模式下的锁不仅需要保证进程可见,还需要考虑进程与锁之间的网络问题。
- 分布式锁还是可以将标记存在内存,只是该内存不是某个进程分配的内存而是公共内存如Redis、Memcache。至于利用数据库、文件等做锁与单机的实现是一样的,只要保证标记能互斥就行。
分布式锁应该具备哪些条件
一个最基本的分布式锁需要满足:
- 互斥:任意一个时刻,锁只能被一个线程持有。
- 高可用:锁服务是高可用的,当一个锁服务出现问题,能够自动切换到另外一个锁服务。并且,即使客户端的释放锁的代码逻辑出现问题,锁最终一定还是会被释放,不会影响其他线程对共享资源的访问。这一般是通过超时机制实现的。
- 可重入:一个节点获取了锁之后,还可以再次获取锁。
除了上面这三个基本条件之外,一个好的分布式锁还需要满足下面这些条件: - 高性能:获取和释放锁的操作应该快速完成,并且不应该对整个系统的性能造成过大影响。
- 非阻塞:如果获取不到锁,不能无限期等待,避免对系统正常运行造成影响。
常见分布式锁实现方案如下:
- 基于关系型数据库比如 MySQL 实现分布式锁。
- 基于分布式协调服务 ZooKeeper 实现分布式锁。
- 基于分布式键值存储系统比如 Redis 、Etcd 实现分布式锁。
关系型数据库的方式一般是通过唯一索引或者排他锁实现。不过,一般不会使用这种方式,问题太多比如性能太差、不具备锁失效机制。
基于 ZooKeeper 或者 Redis 实现分布式锁这两种实现方式要用的更多一些
基于 redis 做分布式锁
1)setnx()
setnx 的含义就是 SET if Not Exists,其主要有两个参数 setnx(key, value)。该方法是原子的,如key 不存在,则设置当前 key 成功,返回 1;如果当前 key 已经存在,则设置当前 key 失败,返回 0。
2)expire()
expire 设置过期时间,要注意的是 setnx 命令不能设置 key 的超时时间,只能通过 expire() 来对key 设置。
3) 使用步骤
1、setnx(lockkey, 1) 如果返回 0,则说明占位失败;如果返回 1,则说明占位成功
2、expire() 命令对 lockkey 设置超时时间,为的是避免死锁问题。
3、执行完业务代码后,可以通过 delete 命令删除 key。
这个方案其实是可以解决日常工作中的需求的,但从技术方案的探讨上来说,可能还有一些可以完善的地方。比如,如果在第一步 setnx 执行成功后,在 expire() 命令执行成功前,发生了宕机的现象,那么就依然会出现死锁的问题,所以如果要对其进行完善的话,可以使用 redis 的 setnx()、get() 和 getset() 方法来实现分布式锁。
(三) 分布式事务
分布式事务是指事务的参与者、支持事务的服务器、资源服务器以及事务管理器分别位于不同的分布式系统的不同节点之上。例如在大型电商系统中,下单接口通常会扣减库存、减去优惠、生成订单 id, 而订单服务与库存、优惠、订单 id 都是不同的服务,下单接口的成功与否,不仅取决于本地的 db 操作,而且依赖第三方系统的结果,这时候分布式事务就保证这些操作要么全部成功,要么全部失败。本质上来说,分布式事务就是为了保证不同数据库的数据一致性。
强一致性
任何一次读都能读到某个数据的最近一次写的数据。系统中的所有进程,看到的操作顺序,都和全局时钟下的顺序一致。简言之,在任意时刻,所有节点中的数据是一样的。
弱一致性
数据更新后,如果能容忍后续的访问只能访问到部分或者全部访问不到,则是弱一致性。
最终一致性
不保证在任意时刻任意节点上的同一份数据都是相同的,但是随着时间的迁移,不同节点上的同一份数据总是在向趋同的方向变化。简单说,就是在一段时间后,节点间的数据会最终达到一致状态。
柔性事务
不同于 ACID 的刚性事务,在分布式场景下基于 BASE 理论,就出现了柔性事务的概念。要想通过柔性事务来达到最终的一致性,就需要依赖于一些特性,这些特性在具体的方案中不一定都要满足,因为不同的方案要求不一样;但是都不满足的话,是不可能做柔性事务的。
幂等操作
在编程中一个幂等操作的特点是其任意多次执行所产生的影响均与一次执行的影响相同。幂等函数,或幂等方法,是指可以使用相同参数重复执行,并能获得相同结果的函数。这些函数不会影响系统状态,也不用担心重复执行会对系统造成改变。例如,支付流程中第三方支付系统告知系统中某个订单支付成功,接收该支付回调接口在网络正常的情况下无论操作多少次都应该返回成功。
分布式事务使用场景
转账
转账是最经典那的分布式事务场景,假设用户 A 使用银行 app 发起一笔跨行转账给用户 B,银行系统首先扣掉用户 A 的钱,然后增加用户 B 账户中的余额。此时就会出现 2 种异常情况:1. 用户 A 的账户扣款成功,用户 B 账户余额增加失败 2. 用户 A 账户扣款失败,用户 B 账户余额增加成功。对于银行系统来说,以上 2 种情况都是不允许发生,此时就需要分布式事务来保证转账操作的成功。
下单扣库存
在电商系统中,下单是用户最常见操作。在下单接口中必定会涉及生成订单 id, 扣减库存等操作,对于微服务架构系统,订单 id 与库存服务一般都是独立的服务,此时就需要分布式事务来保证整个下单接口的成功
同步超时
继续以电商系统为例,在微服务体系架构下,我们的支付与订单都是作为单独的系统存在。订单的支付状态依赖支付系统的通知,假设一个场景:我们的支付系统收到来自第三方支付的通知,告知某个订单支付成功,接收通知接口需要同步调用订单服务变更订单状态接口,更新订单状态为成功。流程图如下,从图中可以看出有两次调用,第三方支付调用支付服务,以及支付服务调用订单服务,这两步调用都可能出现调用超时的情况,此处如果没有分布式事务的保证,就会出现用户订单实际支付情况与最终用户看到的订单支付情况不一致的情况。
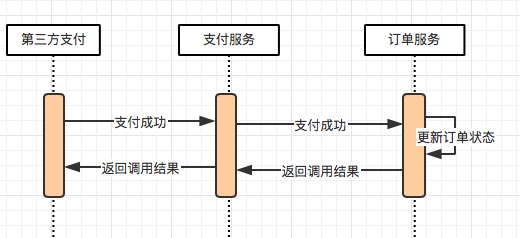
分布式事务的解决方案
1)两阶段提交/XA
两阶段提交,顾名思义就是要分两步提交。存在一个负责协调各个本地资源管理器的事务管理器,本地资源管理器一般是由数据库实现,事务管理器在第一阶段的时候询问各个资源管理器是否都就绪?如果收到每个资源的回复都是 yes,则在第二阶段提交事务,如果其中任意一个资源的回复是 no, 则回滚事务。

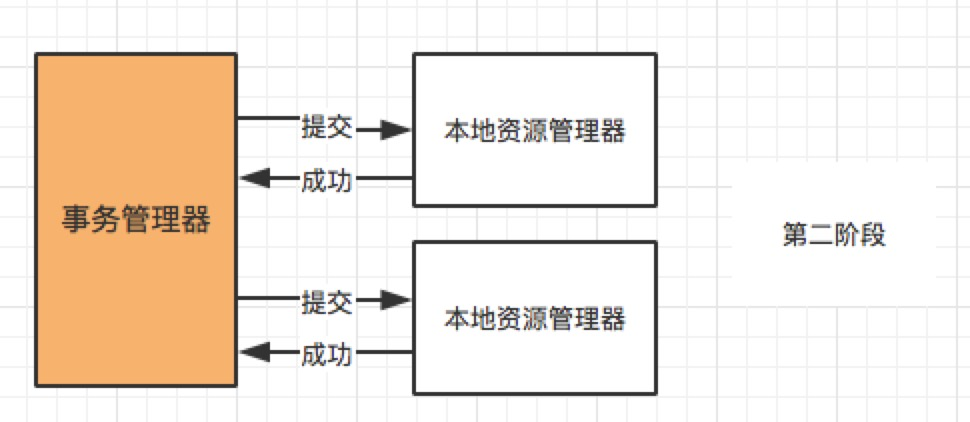
大致的流程:
第一阶段(prepare):事务管理器向所有本地资源管理器发起请求,询问是否是 ready 状态,所有参与者都将本事务能否成功的信息反馈发给协调者;
第二阶段 (commit/rollback):事务管理器根据所有本地资源管理器的反馈,通知所有本地资源管理器,步调一致地在所有分支上提交或者回滚。
存在的问题:
同步阻塞:当参与事务者存在占用公共资源的情况,其中一个占用了资源,其他事务参与者就只能阻塞等待资源释放,处于阻塞状态。
单点故障:一旦事务管理器出现故障,整个系统不可用
数据不一致:在阶段二,如果事务管理器只发送了部分 commit 消息,此时网络发生异常,那么只有部分参与者接收到 commit 消息,也就是说只有部分参与者提交了事务,使得系统数据不一致。
不确定性:当协事务管理器发送 commit 之后,并且此时只有一个参与者收到了 commit,那么当该参与者与事务管理器同时宕机之后,重新选举的事务管理器无法确定该条消息是否提交成功。
本地消息表
本地消息表这个方案最初是 ebay 架构师 Dan Pritchett 在 2008 年发表给 ACM 的文章。该方案中会有消息生产者与消费者两个角色,假设系统 A 是消息生产者,系统 B 是消息消费者,其大致流程如下:
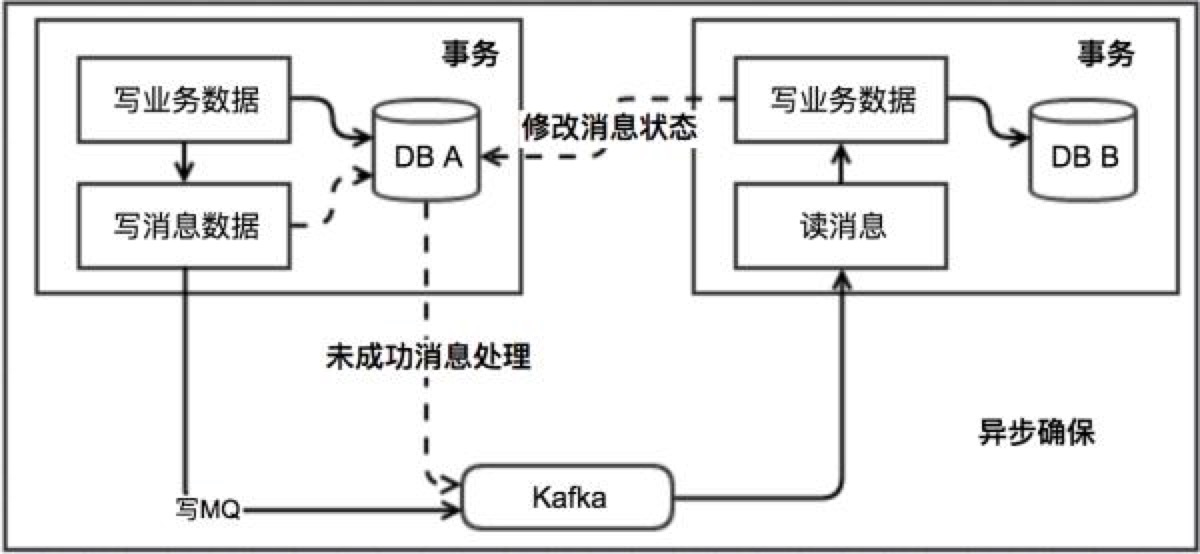
- 当系统 A 被其他系统调用发生数据库表更操作,首先会更新数据库的业务表,其次会往相同数据库的消息表中插入一条数据,两个操作发生在同一个事务中
- 系统 A 的脚本定期轮询本地消息往 mq 中写入一条消息,如果消息发送失败会进行重试
- 系统 B 消费 mq 中的消息,并处理业务逻辑。如果本地事务处理失败,会在继续消费 mq 中的消息进行重试,如果业务上的失败,可以通知系统 A 进行回滚操作
本地消息表实现的条件:
- 消费者与生成者的接口都要支持幂等
- 生产者需要额外的创建消息表
- 需要提供补偿逻辑,如果消费者业务失败,需要生产者支持回滚操作
容错机制:
- 步骤 1 失败时,事务直接回滚
- 步骤 2、3 写 mq 与消费 mq 失败会进行重试
- 步骤 3 业务失败系统 B 向系统 A 发起事务回滚操作
此方案的核心是将需要分布式处理的任务通过消息日志的方式来异步执行。消息日志可以存储到本地文本、数据库或消息队列,再通过业务规则自动或人工发起重试。人工重试更多的是应用于支付场景,通过对账系统对事后问题的处理。
可靠消息最终一致性
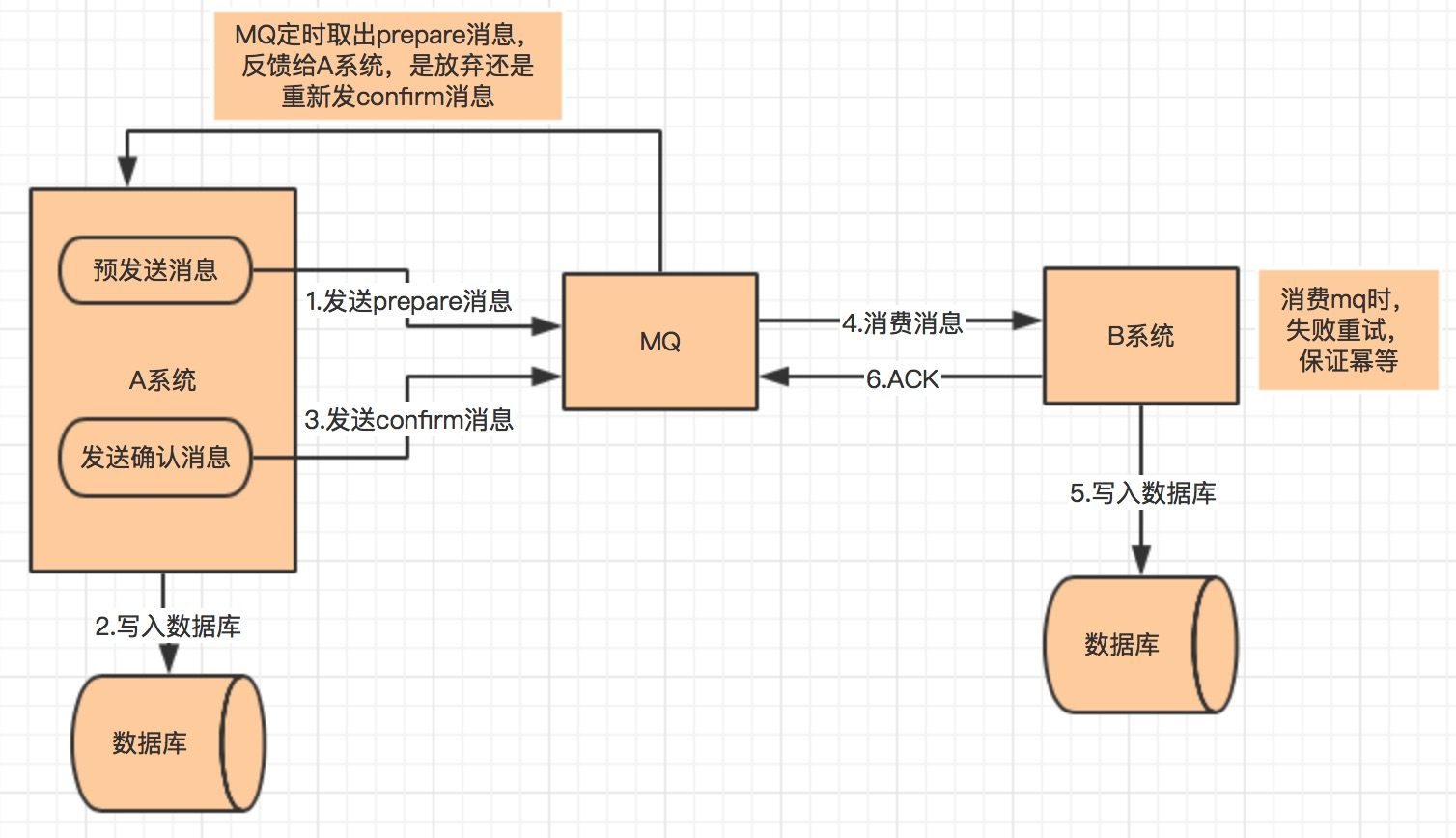
- A 系统先向 mq 发送一条 prepare 消息,如果 prepare 消息发送失败,则直接取消操作
- 如果消息发送成功,则执行本地事务
- 如果本地事务执行成功,则想 mq 发送一条 confirm 消息,如果发送失败,则发送回滚消息
- B 系统定期消费 mq 中的 confirm 消息,执行本地事务,并发送 ack 消息。如果 B 系统中的本地事务失败,会一直不断重试,如果是业务失败,会向 A 系统发起回滚请求
- mq 会定期轮询所有 prepared 消息调用系统 A 提供的接口查询消息的处理情况,如果该 prepare 消息本地事务处理成功,则重新发送 confirm 消息,否则直接回滚该消息
该方案与本地消息最大的不同是去掉了本地消息表,其次本地消息表依赖消息表重试写入 mq 这一步由本方案中的轮询 prepare 消息状态来重试或者回滚该消息替代。其实现条件与余容错方案基本一致。目前市面上实现该方案的只有阿里的 RocketMq。