一次函数

1.1 一次函数

一次函数的定义为：y = kx + b ，k ≠ 0。

​ 注：在这个函数中k代表斜率，b代表与y轴的截距。当 x = 0 时，y = b。

一次函数的性质：

• 可导性
• 连续性
• 增减性（k > 0，单调增；k < 0，单调减）
• 奇偶性（b = 0时，一次函数都为奇函数）

1.2 正比例函数

正比例函数的定义为：y = kx ，k ≠ 0。

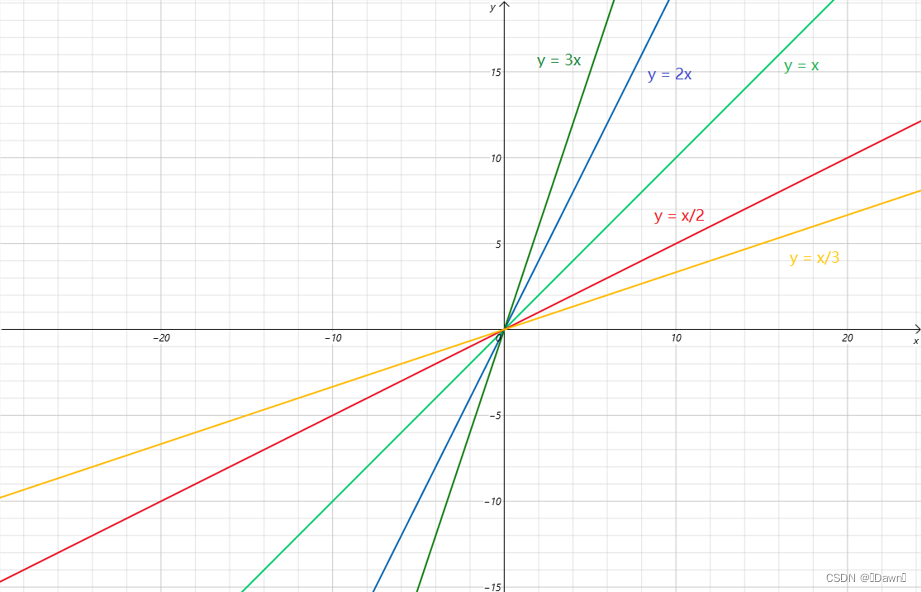
当 K > 0 时的图像规律：

• 图像一定经过原点（0，0）

• k > 0 时，图像向上倾斜，是增函数

• |k|越大，图像越陡；|k|越小，图像越缓

• 奇函数
  

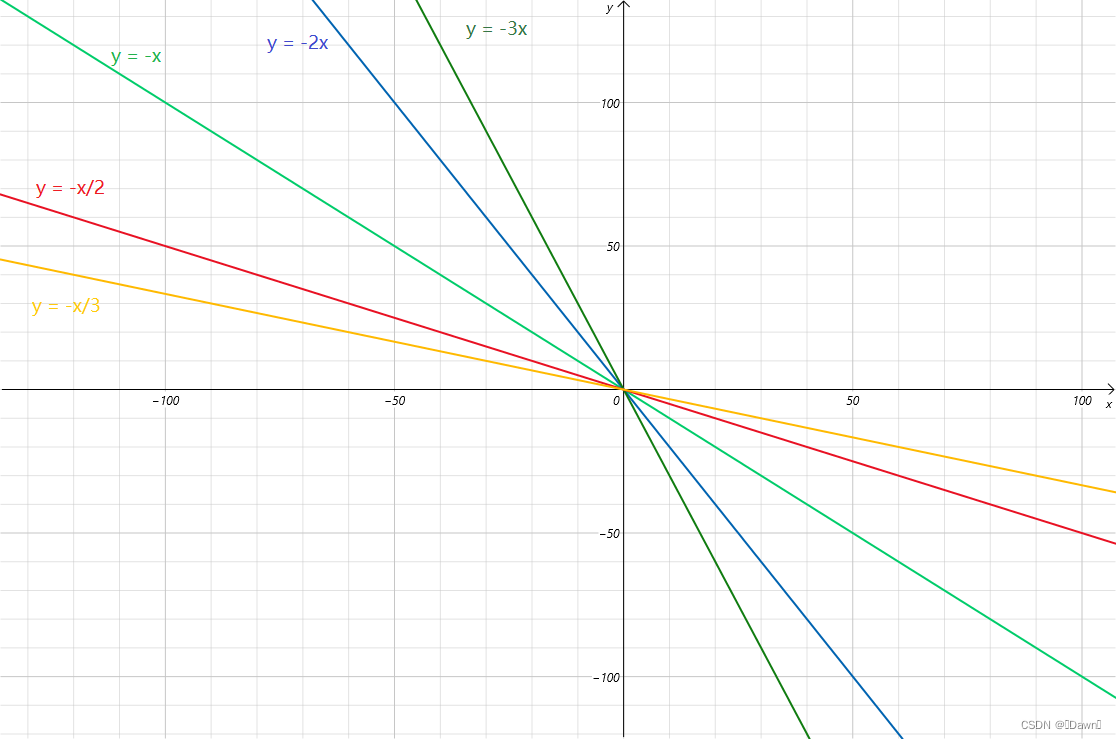
当 K < 0 时的图像规律：

• 图像一定经过原点（0，0）

• k < 0 时，图像向下倾斜，是减函数

• |k|越大，图像越陡；|k|越小，图像越缓

• 奇函数
  

1.3 一次函数的平移

y = kx + b

• k的含义：斜率（直线与x轴夹角的tan值）

• b的含义：截距（直线与y轴的交点）

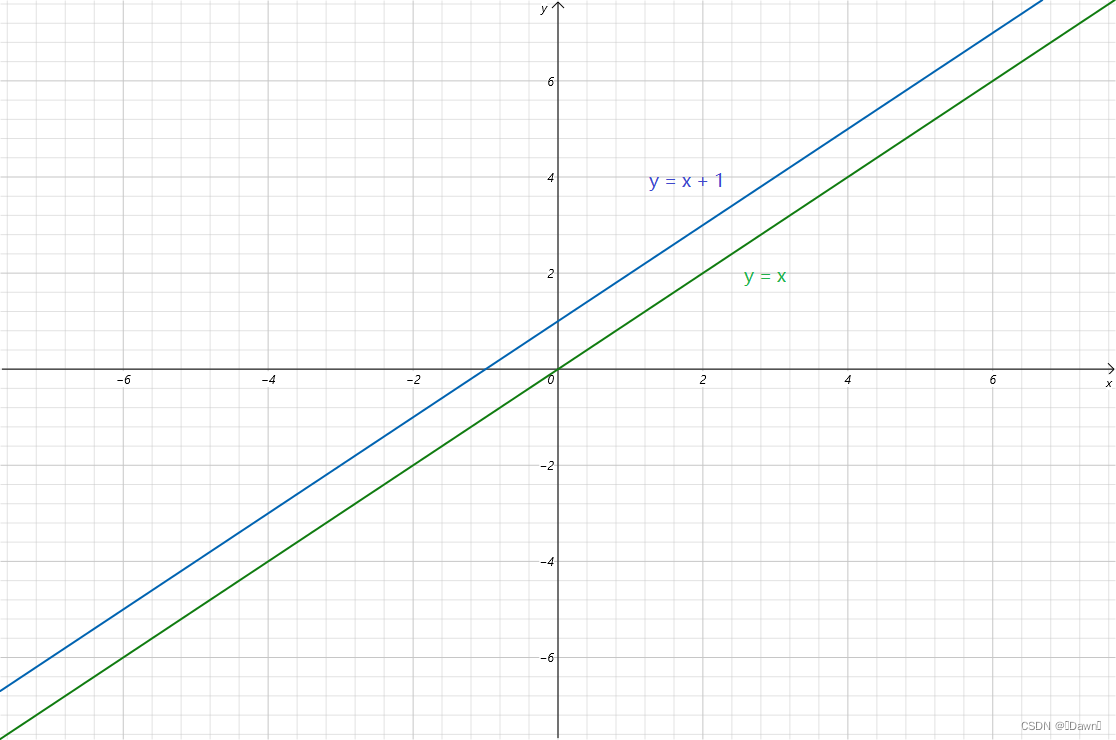
• y = x + 1 是 y = x 向上挪一个单位得来，如下图所示：
  

• 函数的平移：

  • 对于 y（函数整体）来说：上加，下减；
  • 对于 x 来说：左加，右减。
  • 例：y = 3x - 2
    • 向上移动3个单位：y = 3x - 2 + 3
    • 向下移动1个单位：y = 3x - 2 - 1
    • 向左移动2个单位：y = 3(x + 2) - 2
    • 向右移动4个单位：y = 3(x - 4) - 2
    • 向下移动1个单位，向左移动2个单位：y = 3(x + 2) - 2 - 1
    • 向右移动2个单位，向上移动3个单位：y = 3(x - 2) - 2 + 3

1.4 一次函数常用知识

• 已知两点（x₁,y₁），(x₂,y₂)，求斜率k：$k=\frac{y_2-y_1}{x_2-x_1}$
• 点斜式 已知直线过一点（x₀,y₀），斜率为k，求直线方程：y - y₀ = k(x - x₀)
• 两点式 已知直线过两点（x₁,y₁），(x₂,y₂)，求直线方程：$\frac{y-y_1}{x-x_1}$ = $\frac{y_2-y_1}{x_2-x_1}$
• 如果两条直线平行，那么它们的斜率相等
• 如果两条直线垂直（斜率分别为k₁，k₂），那么k₁k₂ = -1