挖坑法，Hoare，非递归法实现快速排序

news2024/9/20 22:31:45

时间：O(N*lgn)->最坏n^2(有序，逆序) 

空间：logN N*2

Hoare 

Hoare法与其他快速排序算法的不同之处在于它使用两个指针（分别指向数组的起始位置和结束位置），并通过交换元素的方式来确定基准值的最终位置。

具体步骤如下：

  1. 选择一个基准值，通常是待排序数组的第一个元素。
  2. 设定两个指针，一个指向数组的起始位置，称为 left，另一个指向数组的结束位置，称为 right。
  3. 从 right 开始，向左移动直到找到一个小于等于基准值的元素。从 left 开始，向右移动直到找到一个大于等于基准值的元素。
  4. 如果 left 指针小于等于 right 指针，则交换这两个元素，然后分别将 left 和 right 指针向后、向前移动一位。
  5. 重复，直到 left 指针大于 right 指针。
  6. 将基准值与 right 指针所指向的元素交换，此时基准值左边的元素都小于等于它，右边的元素都大于等于它。
  7. 对基准值左边和右边的子数组分别递归执行上述步骤，直到每个子数组只有一个元素或为空。

 

    public static int partition2(int[] nums,int left,int right){//Hoare
        int temp=nums[left];
        int i=left;
        while(left<right){

            while(left<right&&nums[right]>=temp){
                right--;
            } while(left<right&&nums[left]<=temp){
                left++;
            }
            int t=nums[left];
            nums[left]=nums[right];
            nums[right]=t;
        }
        int t=nums[i];
        nums[i]=nums[left];
        nums[left]=t;

        return left;
    }

 

挖坑 

具体步骤如下：

  1. 选择一个基准值，通常是待排序数组的第一个元素。
  2. 从数组的右端开始，设定一个指针 right 指向最右边的元素，然后从右往左扫描数组，找到第一个小于基准值的元素，将该元素填入基准值所在的位置，即将基准值挖空形成一个坑。
  3. 接着从数组的左端开始，设定一个指针 left 指向最左边的元素，然后从左往右扫描数组，找到第一个大于基准值的元素，将该元素填入上一步挖空的坑中，并将该元素所在的位置再次挖空。
  4. 重复步骤2和步骤3，直到 left 和 right 指针相遇。
  5. 将基准值填入最后一个挖空的坑中，此时基准值左边的元素都比它小，右边的元素都比它大。
  6. 对基准值左边和右边的子数组分别递归执行上述步骤，直到每个子数组只有一个元素或为空。

挖坑法快速排序的核心思想是通过挖空和填坑的方式，将待排序数组划分为左右两个部分，左边部分的元素都小于基准值，右边部分的元素都大于基准值，然后对左右子数组进行递归排序，最终完成整个数组的排序。

import java.util.Arrays;

/**
 * Created with IntelliJ IDEA.
 * Description:
 * User: 86180
 * Date: 2023-10-28
 * Time: 1:38
 */

public class sort {
    public static void quickSort(int[] nums){
        quick(nums,0,nums.length-1);


    }
    public static void quick(int[] nums,int start,int end){
        if(start>=end){//1 2 3 4 s=0,e=-1
            return;
        }
        int pivot=partition(nums,start,end);
        quick(nums,start,pivot-1);
        quick(nums,pivot+1,end);


    }
    public static int partition(int[] nums,int left,int right){
        int temp=nums[left];
        while(left<right){
            while(left<right&&nums[right]>=temp){//>=是为了6，1，2，6的情况，不加=会导致6和6一直在交换。
                right--;
            }
            nums[left]=nums[right];
            while(left<right&&nums[left]<=temp){//left<right是解决1,2,3的情况
                left++;
            }
            nums[right]=nums[left];
        }
        nums[left]=temp;//l和r相遇。
        System.out.println(Arrays.toString(nums));

        return left;//相遇位置就是基准。
    }

    public static void main(String[] args) {
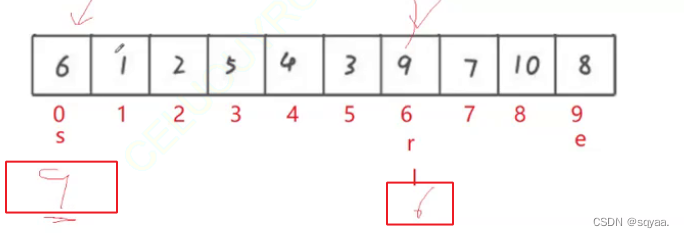
        int[] nums={6,1,2,7,9,3,4,5,10,8};
        quickSort(nums);
        System.out.println(Arrays.toString(nums));
    }
}

每次进行快排的结果

[5, 1, 2, 4, 3, 6, 9, 7, 10, 8]
[3, 1, 2, 4, 5, 6, 9, 7, 10, 8]
[2, 1, 3, 4, 5, 6, 9, 7, 10, 8]
[1, 2, 3, 4, 5, 6, 9, 7, 10, 8]
[1, 2, 3, 4, 5, 6, 8, 7, 9, 10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

 

 

 

 

 

 

 

 

 

问题

为啥左边作为基准，就要从右边先开始？

就比如我们把Hoare中的代码，

while (left < right && nums[left] <= temp) { left++; }放在

while (left < right && nums[right] >= temp) { right--; }

前面就会出问题得到不是我们想要的代码

 

6,1,2,7,9,3,4,5,10,8

如果我们先移动 `left` 指针，那么 `left` 指针会一直向右移动，直到找到一个比基准值大的元素或者 `left` 和 `right` 指针相遇。这样会导致 `left` 指针停在一个比基准值大的位置上，而 `right` 指针可能停在一个比基准值小的位置上，违反了我们的划分目标。

 

第一次快排，最后r指针最后会停在一个比6大地方，l++，会导致l和r相遇，此时nums[l]=nums[r]>6,交换6和9就导致了左边出现比6大的数字

330e36f843f346c78b82c3a8c7aedf42.png

为啥还要对快排进行优化

对快速排序进行优化的主要目的是提高其在各种情况下的性能和效率。尽管快速排序通常是一种高效的排序算法，但在某些情况下，它可能会出现性能下降的情况。下面是一些导致性能下降的情况：

  1. 已排序或近乎有序的数组：如果输入数组已经是有序的或近乎有序的，传统的快速排序算法可能会导致分割不均匀，使得递归调用的层数变多，从而降低了性能。

  2. 大量重复元素的数组：当待排序的数组包含大量重复元素时，传统的快速排序算法可能会导致分割不均匀。这是因为传统算法只考虑基准元素的大小，而没有考虑相等元素的情况，从而导致划分不均匀，影响性能。

  3. 小规模子数组：当待排序的子数组变得很小（通常小于一定阈值）时，快速排序的递归调用开销可能会超过插入排序的开销。在这种情况下，使用插入排序或其他简单排序算法可能更加高效。

  4. 递归调用栈溢出：传统的快速排序算法使用递归来处理子数组，当待排序的数组规模非常大时，递归调用栈可能会溢出，导致程序崩溃。这种情况可以通过尾递归优化或迭代方式实现来解决。

以上情况中的任何一种都可能导致快速排序的性能下降。为了克服这些问题，可以采取相应的优化措施，如随机选择基准元素、三数取中法。

 

三数取中

    private static void sort1(int[] array,int start,int end){
        //防止只有左子树或者右子树的情况
        if(start >= end){
            return;
        }
        //在找基准之前，解决划分不均匀的问题,将关键值改变为中间大小的值后，能解决单分支的情况
        int index = findMidValOfIndex(array,start,end);
        swap(array,start,index);
 
        int povit = partion(array,start,end);
        sort(array,start,povit-1);
        sort(array,povit+1,end);
    }
    /*
    找到中位数
     */
    private static int findMidValOfIndex(int[] array,int start,int end){
        int midIndex = (start+end)/2;
 
        if(array[start] < array[end]){
            if(array[midIndex] < array[start]) {
                return start;
            } else if (array[end] < array[midIndex]) {
                return end;
            }
            else {
                return midIndex;
            }
        }
        else {
            if (array[midIndex] > array[start]){
                return start;
            } else if (array[midIndex] < array[end]) {
                return end;
            }
            else {
                return midIndex;
            }
        }
    }

 随机选基准

private static void sort2(int[] array,int start,int end){
        //防止只有左子树或者右子树的情况
        if(start >= end){
           return;
        }
        if(( end-start+1) <= 15){
        //插入排序减少后几层 的递归
            insertSort1(array,start,end);
        }
        //在找基准之前，解决划分不均匀的问题,将关键值改变为中间大小的值后，能解决单分支的情况
        int index = findMidValOfIndex(array,start,end);
        swap(array,start,index);
 
        int povit = partion(array,start,end);
        sort(array,start,povit-1);
        sort(array,povit+1,end);
    }
    public static void insertSort1(int[] array,int left,int right){
        for (int i = left+1; i <= right ; i++) {
            int j = i-1;
            int tmp = array[i];
            for (; j >= left ; j--) {
                if(array[j] > array[i]){
                    array[j+1] = array[j];
                }
                else{
                    break;
                }
            }
            array[j+1] = tmp;
        }
    }

非递归实现快排

import java.util.Stack;

public class QuickSortNonRecursive {
    public static void quickSort(int[] arr) {
        if (arr == null || arr.length <= 1) {
            return;
        }
        
        Stack<Integer> stack = new Stack<>();
        stack.push(0);
        stack.push(arr.length - 1);
        
        while (!stack.isEmpty()) {
            int end = stack.pop();
            int start = stack.pop();
            
            int pivotIndex = partition(arr, start, end);
            
            if (pivotIndex - 1 > start) {
                stack.push(start);
                stack.push(pivotIndex - 1);
            }
            
            if (pivotIndex + 1 < end) {
                stack.push(pivotIndex + 1);
                stack.push(end);
            }
        }
    }
    
    private static int partition(int[] arr, int start, int end) {
        int pivot = arr[end];
        int i = start - 1;
        
        for (int j = start; j < end; j++) {
            if (arr[j] < pivot) {
                i++;
                swap(arr, i, j);
            }
        }
        
        swap(arr, i + 1, end);
        return i + 1;
    }
    
    private static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    
    public static void main(String[] args) {
        int[] arr = {5, 2, 9, 1, 7, 6, 8};
        quickSort(arr);
        
        for (int num : arr) {
            System.out.print(num + " ");
        }
    }
}

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1144702.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

python 安装成功后终端显示的还是低版本

python 安装成功后终端显示的还是低版本

如果你下载了新版的 Python&#xff0c;但在使用时发现仍然是之前的版本&#xff0c;可能是因为新版的 Python 没有替代系统环境中的旧版 Python。 检查 PATH 环境变量&#xff1a;在命令行中输入 python --version 来查看当前默认的 Python 版本。如果显示的是旧版 Python 的…
阅读更多...
Zotero背景设置护眼模式

Zotero背景设置护眼模式

一、背景知识 Zotero是开源的文献管理工具&#xff0c;功能非常强大&#xff0c;可以安装多款插件。对我来说&#xff0c;其最大的优点是可以对文章分类和打标签&#xff0c;因为某个瞬间&#xff0c;我经常想起论文中的一个图片&#xff0c;或者某个细节&#xff0c;但是却记…
阅读更多...
Android：窗口管理器WindowManager

Android：窗口管理器WindowManager

Android&#xff1a;窗口管理器WindowManager 导言 本篇文章主要是对Android中与窗口(Window)有关的知识的介绍&#xff0c;主要涉及到的有&#xff1a; WindowWindowManagerWindowManagerService 主要是为了更进一步地向下地深入Android屏幕渲染的知识&#xff08;虽然窗口…
阅读更多...
vlc打开网络流（如rtmp），并查看媒体信息

vlc打开网络流（如rtmp），并查看媒体信息

打开vlc 选择媒体&#xff0c;打开网络串流 输入rtmp地址&#xff0c;点击播放 选择工具-编解码信息 可以查看节目的编码信息什么的
阅读更多...
口袋参谋：如何快速挑选宝贝核心关键词？三种方法，简单有效！

口袋参谋：如何快速挑选宝贝核心关键词？三种方法，简单有效！

做电商&#xff0c;一定要会选择关键词&#xff01;这是我近十年做电商的经验之谈。 不管是标题还是直通车推广&#xff0c;都需要选择与产品相关度高、符合买家搜索习惯的关键词&#xff0c;只有这样&#xff0c;才能吸引更多自然流量&#xff01;有了流量加持&#xff0c;还…
阅读更多...
C#学习相关系列之多线程（七）---Task的相关属性用法

C#学习相关系列之多线程（七）---Task的相关属性用法

一、Task和Thread的区别 任务是架构在线程之上的,任务最终的执行还是要给到线程去执行的。任务和线程之间不是一对一的关系&#xff0c;任务更像线程池&#xff0c;任务相比线程池有很小的开销和精确的控制。&#xff08;总的来说Task的用法更为先进&#xff0c;在多线程的时候…
阅读更多...
人工智能基础_机器学习008_使用正规方程_损失函数进行计算_一元一次和二元一次方程演示_sklearn线性回归演示---人工智能工作笔记0048

人工智能基础_机器学习008_使用正规方程_损失函数进行计算_一元一次和二元一次方程演示_sklearn线性回归演示---人工智能工作笔记0048

自然界很多都是正态分布的,身高,年龄,体重...但是财富不是. 然后我们来看一下这个y = wx+b 线性回归方程. 然后我们用上面的代码演示. 可以看到首先import numpy as np 导入numby 数据计算库 import matplotlib.pyplot as plt 然后导入图形画的库 然后: X = np.linspace(0,…
阅读更多...
【计算机毕设经典案例】基于微信小程序的图书管理系统

【计算机毕设经典案例】基于微信小程序的图书管理系统

前言&#xff1a;我是IT源码社&#xff0c;从事计算机开发行业数年&#xff0c;专注Java领域&#xff0c;专业提供程序设计开发、源码分享、技术指导讲解、定制和毕业设计服务 &#x1f449;IT源码社-SpringBoot优质案例推荐&#x1f448; &#x1f449;IT源码社-小程序优质案例…
阅读更多...
数组与链表算法-数组与多项式

数组与链表算法-数组与多项式

目录 数组与链表算法-数组与多项式 多项式数组表达式 C代码 数组与链表算法-数组与多项式 多项式是数学中相当重要的表达方式&#xff0c;如果使用计算机来处理多项式的各种相关运算&#xff0c;那么通常使用数组或链表来存储多项式。 多项式数组表达式 假如一个多项&…
阅读更多...
网络安全（黑客技术）—小白自学

网络安全（黑客技术）—小白自学

目录 一、自学网络安全学习的误区和陷阱 二、学习网络安全的一些前期准备 三、网络安全学习路线 四、学习资料的推荐 想自学网络安全&#xff08;黑客技术&#xff09;首先你得了解什么是网络安全&#xff01;什么是黑客&#xff01; 网络安全可以基于攻击和防御视角来分类&am…
阅读更多...
PostgreSQL 基础知识

PostgreSQL 基础知识

执行环境&#xff1a; psql 1. 创建一个表格 CREATE TABLE customers ( customer_id serial PRIMARY KEY,firstname VARCHAR(100) NOT NULL,lastname VARCHAR(100) NOT NULL,username VARCHAR(50) UNIQUE NOT NULL,password VARCHAR(50) NOT NULL,email VARCHAR(255) UNIQUE …
阅读更多...
Go学习第十三章——Gin（请求与响应）

Go学习第十三章——Gin（请求与响应）

Go web框架——Gin&#xff08;请求与响应&#xff09; 1 响应1.1 String1.2 JSON&#xff08;*&#xff09;1.3 HTML&#xff08;*&#xff09;1.4 XML1.5 文件&#xff08;*&#xff09; 2 请求2.1 请求参数查询参数 (Query)动态参数 (Param)表单参数 (PostForm)原始参数 (Ge…
阅读更多...
[导弹打飞机H5动画制作]飞机路线的随机起飞及自爆模拟

[导弹打飞机H5动画制作]飞机路线的随机起飞及自爆模拟

参考代码&#xff1a; this.btnOff.addEventListener("click", off.bind(this)); this.btnBomb.addEventListener("click", bomb.bind(this)); var _this this; var pb null; function off() {if (pb null) {pb new lib.sb1link();pb.x 600;pb.y 30…
阅读更多...
Spring Cloud：三【详细】

Spring Cloud：三【详细】

目录 Http客户端Feign Feign的使用 Feign自定义配置 第一种方式 第二种方式 Feign的优化 Feign最佳实践方式 实现一 实现二 Http客户端Feign RestTemplate缺点是&#xff0c;url不统一&#xff0c;编写困难&#xff0c;可读性差&#xff0c;参数复杂难以维护。 这时…
阅读更多...
【计算机网络笔记】DNS报文格式

【计算机网络笔记】DNS报文格式

DNS 提供域名到主机IP地址的映射  域名服务的三大要素&#xff1a;  域&#xff08;Domain&#xff09;和域名(Domain name)&#xff1a; 域指由地 理位置或业务类型而联系在一起的一组计算机构 成。  主机&#xff1a;由域名来标识。域名是由字符和&#xff08;或&a…
阅读更多...
刚刚：腾讯云3年轻量2核2G4M服务器优惠价格366元三年

刚刚：腾讯云3年轻量2核2G4M服务器优惠价格366元三年

腾讯云3年轻量2核2G4M服务器&#xff0c;2023双十一优惠价格366元三年&#xff0c;自带4M公网带宽&#xff0c;下载速度可达512KB/秒&#xff0c;300GB月流量&#xff0c;50GB SSD盘系统盘&#xff0c;腾讯云百科txybk.com分享腾讯云轻量2核2G4M服务器性能、优惠活动、购买条件…
阅读更多...
雷电_安卓模拟器安装burpsuit_CA证书

雷电_安卓模拟器安装burpsuit_CA证书

雷电_安卓模拟器安装burpsuit_CA证书 文章目录 雷电_安卓模拟器安装burpsuit_CA证书雷电模拟器官网&#xff1a;https://www.ldmnq.com 安装burpsuit证书1 打开雷电模拟器右上角的winfi图标 -->点击齿轮2 修改网络3 选择高级 —》手动4 查看真实机IP的地址&#xff0c;选择虚…
阅读更多...
超分辨率重建——SESR网络训练并推理测试（详细图文教程）

超分辨率重建——SESR网络训练并推理测试（详细图文教程）

最近学了一个超轻量化的超分辨率重建网络SESR&#xff0c;效果还不错。 目录 一、 源码包二、 数据集的准备2.1 官网下载2.2 网盘下载 三、 训练环境配置四、训练4.1 修改配置参数4.2 导入数据集4.3 2倍超分网络训练4.3.1 训练SESR-M5网络4.3.2 训练SESR-M5网络4.3.3 训练SESR…
阅读更多...
Kitex踩坑 [Error] KITEX: processing request error,i/o timeout

Kitex踩坑 [Error] KITEX: processing request error,i/o timeout

报错问题 2023/010/28 17:20:10.250768 default_server_handler.go:234: [Error] KITEX: processing request error, remoteService, remoteAddr127.0.0.1:65425, errordefault codec read failed: read tcp 127.0.0.1:8888->127.0.0.1:65425: i/o timeout 分析原因 Hert…
阅读更多...
【刷题笔记10.28】Leetcode：使括号有效的最少添加

【刷题笔记10.28】Leetcode：使括号有效的最少添加

Leetcode&#xff1a;使括号有效的最少添加 上代码 方法一&#xff1a;使用Deque 双向队列 /*** 方法一&#xff1a;使用Deque 双向队列* param s* return*/public int minAddToMakeValid(String s) {//1、将括号字符串转换为char[] 字符数组char[] data s.toCharArray();//2…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023