目录

数组与链表算法-数组与多项式

多项式数组表达式

C++代码

---

数组与链表算法-数组与多项式

多项式是数学中相当重要的表达方式，如果使用计算机来处理多项式的各种相关运算，那么通常使用数组或链表来存储多项式。

多项式数组表达式

假如一个多项，这个多项式就被称为次多项式。一个多项式如果使用数组结构存储在计算机中的话，表示法有以下两种：

（1）使用一个长度的一维数组来存放，数组的第一个位置存储多项式的最大指数，数组之后的各个位置从指数开始，依次递减按序存储对应项的系数：

        

存储在中，例如，可转换为A数组来表示，例如：

        

使用这种表达法的优点是在计算机中运用时，对于多项式各种运算（如加法与乘法）的设计比较方便。不过，如果多项式的系数为多半为零，例如，就太浪费内存空间了。

C++代码

#include<iostream>
using namespace std;

void PolySum(int* arrA, int* arrB, int* arrResoult) {
	arrResoult[0] = arrA[0];
	for (int i = 1; i < arrA[0] + 2; i++) {
		arrResoult[i] = arrA[i] + arrB[i];		
	}
}

void PrintPoly(int* arr) {
	int MaxExp = arr[0];
	for (int i = 1; i < arr[0] +2; i++) {
		if (arr[i] != 0) {
			if (MaxExp != 0)
				cout << arr[i] << "X^" << MaxExp << " ";
			else
				cout << arr[i];
			if (MaxExp - 1 >= 0)
				cout << " + ";
		}
		MaxExp--;
	}
	cout << endl;
}

int main() {
	int* PolyA = new int[]{ 4,3,7,0,6,2 };
	int* PolyB = new int[]{ 4,1,5,2,0,9 };
	int* PolyResoult = new int[PolyA[0]+2] {0};
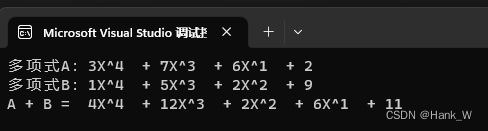
	cout << "多项式A：";
	PrintPoly(PolyA);
	cout << "多项式B：";
	PrintPoly(PolyB);
	PolySum(PolyA, PolyB, PolyResoult);
	cout << "A + B =  ";
	PrintPoly(PolyResoult);
	return 0;
}

输出结果

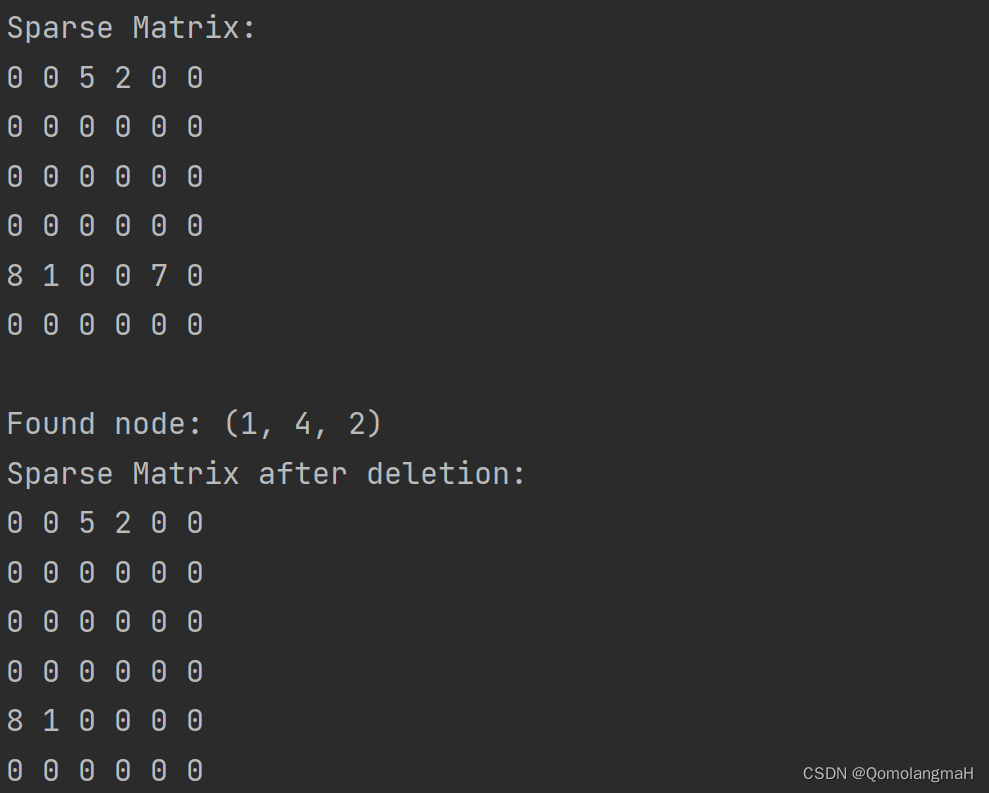
（2）只存储多项式中的非零项。如果有个非零项，就使用长的数组来存储每一个非零项的指数及系数，但数组的第一个元素存储的是这个多项式非零项的个数。

例如，可表示成数组，如下所示：

        

这种方法的优点是在多项式零项较多时可以减少对内存空间的浪费，但缺点是在为多项式设计各种运算时会复杂许多。

使用多项式的两种数组表示法来存储多项式，结果如下：

•  
• 

注意，在上面这个例子中，第二种数组表示法并没有体现出减少对内存空间的浪费的优点，这是因为多项式的零项并不多，只是缺了和这两项。