本文采用Python及PyTorch版本如下:
-
Python:3.9.0
-
PyTorch:2.0.1+cpu
本文为博主自用知识点提纲,无过于具体介绍,详细内容请参考其他文章。
线性代数 & 微积分
- 1. 线性代数
- 1.1 基础
- 1.1.1 标量
- 1.1.2 向量
- 长度(维度)、形状
- 1.1.3 矩阵
- 1.1.3.1 迹
- 1.1.3.2 转置矩阵
- 1.1.3.3 特征值
- 1.1.3.4 奇异值
- 1.1.3.5 逆矩阵
- 1.1.3.6 Moore-Penrose伪逆
- 1.1.4 张量
- 1.2 向量空间
- 1.3 运算
- 1.3.1 加 & 减
- 1.3.2 内积 & 点积
- 1.3.2.1 内积
- 1.3.2.1 点积
- 1.3.3 外积 & 克罗内克积
- 1.3.4 哈达玛积
- 1.3.5 矩阵乘积
- 1.3.6 向量-向量叉积
- 1.4 范数
- 1.5 距离(向量距离)
- 1.6 余弦相似度
- 1.7 矩阵分解
- 1.7.1 矩阵三角分解(LR / LU分解)
- 1.7.2 矩阵正交三角分解(QR分解)
- 1.7.3 矩阵特征值分解(EVD分解)
- 1.7.4 矩阵奇异值分解(SVD分解)
- 1.8 降维
- 1.8.1 基础操作
- 1.8.1.1 求和
- 1.8.1.2 平均值
- 1.8.2 PCA主成分分析
- 1.8.3 稀疏矩阵压缩
- 2. 微积分
- 2.1 导数 & 微分
- 2.2 偏导数
- 2.3 梯度
- 2.4 Hessian矩阵
- 2.5 Jacobian矩阵
1. 线性代数
线性代数是数学的一个分支,它的研究对象是向量、向量空间(线性空间)、线性变换及有限维的线性方程组。线性代数已被广泛地应用于自然科学和社会科学中。
- 线性(Linear)指量与量之间按比例、成直线的关系,在数学上可以理解为一阶导数为常数的函数。
- 非线性(Non-Linear)则相反,即量与量之间不按比例、不成直线的关系,一阶导数不为常数的函数。
1.1 基础
1.1.1 标量
在数学中,标量(Scalar):亦称作“无向量”,只具有数值大小,没有方向,但有正负之分。
在Python中,标量即为普通的数字类型,包括int(整型)、float(浮点型)、bool(布尔型)和complex(复数)。
在数学定义中,标量等价于零阶张量;在PyTorch中也是如此,但零阶张量被表示为为仅包含一个数字的torch.Tensor类型(等价于仅包含一个元素的列表),并不完全等价于数学上的普通标量(单个数字)。
import torch
x = torch.tensor(3.0)
y = torch.tensor(2.0)
x + y, x * y, x / y, x ** y

1.1.2 向量
在数学中,向量(Vector,亦称欧几里得向量、几何向量),指具有大小(magnitude)和方向的量,形式上表现为以原点为始点箭头指向终点的坐标。向量一般表示为带箭头的线段,表示其方向;印刷体一般为加粗体字母。
数学表示法用x∈ℝn表示向量。
印刷体:
x
=
[
x
1
x
2
x
3
⋮
x
n
]
\boldsymbol{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots\\ x_n \\ \end{bmatrix}
x=
x1x2x3⋮xn
手写体:
x
→
=
[
x
1
x
2
x
3
⋮
x
n
]
\overrightarrow{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots\\ x_n \\ \end{bmatrix}
x=
x1x2x3⋮xn
在Python中,向量可以视作由标量值组成的列表,其中的标量值被称作向量的元素(element)或分量(component)。一般可用向量表示数据集中的样本。
在数学定义中,向量等价于一阶张量,在PyTorch中也是如此。
x = torch.arange(4)
x

我们可以通过索引访问元素,获得的元素仍为PyTorch标量(即<class 'torch.Tensor'>类型)。
x[3]

长度(维度)、形状
向量的长度与维度等价,我们可以通过Python的内置函数len来访问其长度。
len(x)

当张量为一阶张量(向量)时,我们可以通过shape属性访问其长度。
x.shape

维度之分:
- 张量:张量维度指张量的轴数(阶数)
- 向量:向量维度指元素的数量(长度)
1.1.3 矩阵
在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合。
在Python与数学中,矩阵同样代表二阶张量,以及向量的向量。
数学表示法用A∈ℝm×n来表示矩阵A,即用大写字母来表示矩阵,其中每个元素aij属于第i行第j列。
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} A= a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn
A的形状为(m,n)或m×n,当m=n时,其被称作方阵(Square Matrix)。
我们可以通过调用函数创建一个5×4的矩阵。
A = torch.arange(20).reshape(5, 4)
A

与向量相同,我们可以通过索引访问元素,获得的元素仍为PyTorch标量(即<class 'torch.Tensor'>类型)。
A[3, 3]

1.1.3.1 迹
迹(trace)运算是方阵对角元素的和:
T
r
(
A
)
=
∑
i
A
i
,
i
Tr(A)=\sum_{i}A_{i,i}
Tr(A)=i∑Ai,i
代码如下:
D = torch.arange(16).reshape(4,4)
D.trace()

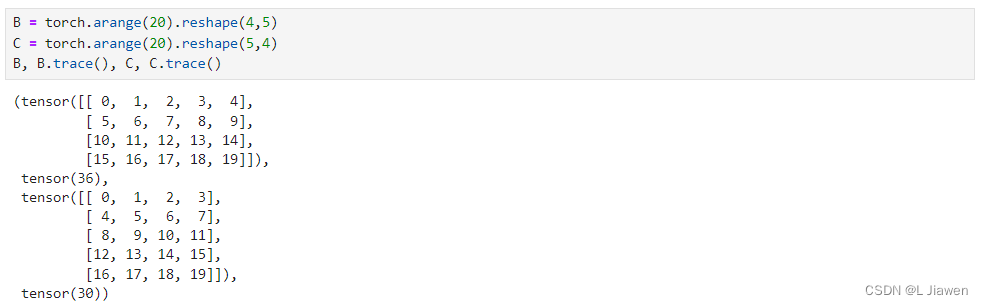
在PyTorch中,非方阵迹计算规则如下:
代码如下:
B = torch.arange(20).reshape(4,5)
C = torch.arange(20).reshape(5,4)
B, B.trace(), C, C.trace()
1.1.3.2 转置矩阵
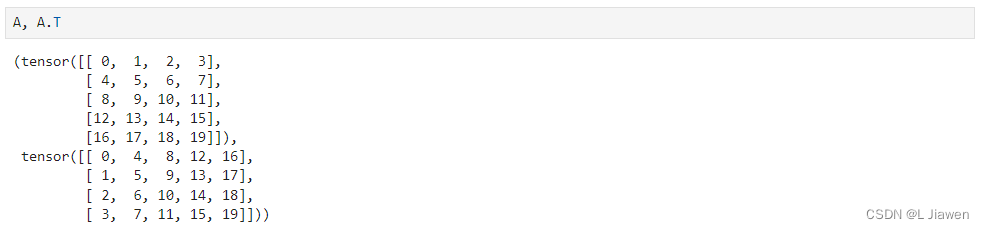
当交换矩阵的行、列时,结果称为矩阵的转置(transpose),一般使用 A T A^{T} AT表示矩阵 A A A的转置。
A T = [ a 11 a 21 ⋯ a m 1 a 12 a 22 ⋯ a m 2 ⋮ ⋮ ⋱ ⋮ a 1 n a 2 n ⋯ a m n ] A^T = \begin{bmatrix} a_{11} & a_{21} & \cdots & a_{m1} \\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \end{bmatrix} AT= a11a12⋮a1na21a22⋮a2n⋯⋯⋱⋯am1am2⋮amn
可以通过如下代码访问其转置。
A.T
当 A = A T A=A^{T} A=AT时,将 A A A矩阵称为对称矩阵(Systematic Matrix)。
1.1.3.3 特征值
特征值:指设 A A A是n阶方阵,如果存在数m和非零n维列向量x,使得 A x = λ x Ax=λx Ax=λx成立,则称λ是 A A A的一个特征值(characteristic value)或本征值(eigenvalue)。特征值分解可对满秩方阵进行分解。
具体内容见:特征值分解
1.1.3.4 奇异值
奇异值是矩阵里的概念,一般通过奇异值分解定理求得。设 A A A为m*n阶矩阵,q=min(m,n), A A T AA^{T} AAT的q个非负特征值的算术平方根叫作A的奇异值。奇异值分解是线性代数和矩阵论中一种重要的矩阵分解法,适用于信号处理和统计学等领域。
具体内容见:奇异值分解
1.1.3.5 逆矩阵
设A是一个n阶矩阵,若存在另一个n阶矩阵B,使得: AB=BA=I ,则称方阵A可逆,并称方阵B是A的逆矩阵。
A
B
=
B
A
=
I
A
T
=
B
AB=BA=I\\ A^{T}=B
AB=BA=IAT=B
求逆矩阵代码如下:
# 矩阵求逆一般建议使用double或float浮点型,否则无法表示元素为小数的逆矩阵
F = torch.tensor([[1., 2, 3], [0, 4, 5], [0, 0, 6]])
F.inverse()

1.1.3.6 Moore-Penrose伪逆
对于非方阵,其逆矩阵没有定义,但我们希望通过
A
∈
R
m
×
n
A\in \mathbb{R^{m×n}}
A∈Rm×n的左逆
B
B
B求解线性方程:
A
x
=
y
Ax=y
Ax=y
即:
x
=
B
y
x=By
x=By
Moore-Penrose伪逆(Moore-Penrose广义逆)定义如下:
A
+
=
lim
α
→
0
(
A
T
A
+
α
I
)
−
1
A
T
=
V
D
+
U
T
A^{+}=\lim_{\alpha→0}(A^{T}A+\alpha I)^{-1}A^{T}=VD^{+}U^{T}
A+=α→0lim(ATA+αI)−1AT=VD+UT
其中,矩阵 U U U、 D D D和 V V V是矩阵 A A A的奇异值分解后得到的矩阵。对角矩阵 D D D的伪逆 D + D^{+} D+是其非零元素取倒数再转置得到的。
对于矩阵 A ∈ R m × n A\in \mathbb{R^{m×n}} A∈Rm×n:
- 当 m < n m<n m<n时(行数<列数),方程可能有多个解, x = A + y \boldsymbol{x}=A^{+}y x=A+y是所有可行解中L2范数 ∣ ∣ x ∣ ∣ 2 ||x||_2 ∣∣x∣∣2最小的解。
- 当 m > n m>n m>n时(列数<行数),方程可能没有解, x = A + y \boldsymbol{x}=A^{+}y x=A+y可使得 A x Ax Ax和 y y y的L2距离 ∣ ∣ A x − y ∣ ∣ 2 ||Ax-y||_2 ∣∣Ax−y∣∣2最小。
1.1.4 张量
张量是一个更为一般的定义,其用特殊字体的大写字母表示( X \textsf{X} X),低阶张量与上述三种量的等价关系如下:
-
零阶张量:标量(Scalar)
-
一阶张量:向量(Vector)
-
二阶张量:矩阵(Matrix)
我们同样可以使用类似的方式创建高阶张量,并通过索引访问其中的元素,获得的元素仍为PyTorch标量(即<class 'torch.Tensor'>类型)。
X = torch.arange(24).reshape(2, 3, 4)
print(X)
print(X[0, 1, 2])

1.2 向量空间
向量空间亦称线性空间,它是线性代数的中心内容和基本概念之一。
设V是一个非空集合,P是一个域。若:
1.在V中定义了一种运算,称为加法,即对V中任意两个元素α与β都按某一法则对应于V内惟一确定的一个元素α+β,称为α与β的和。
2.在P与V的元素间定义了一种运算,称为数乘(亦称数量乘法),即对V中任意元素α和P中任意元素k,都按某一法则对应V内惟一确定的一个元素kα,称为k与α的积。
3.加法与纯量乘法满足以下条件:
(1)α+β=β+α,对任意α,β∈V.
(2)α+(β+γ)=(α+β)+γ,对任意α,β,γ∈V.
(3)存在一个元素0∈V,对一切α∈V有α+0=α,元素0称为V的零元.
(4)对任一α∈V,都存在β∈V使α+β=0,β称为α的负元素,记为-α.
(5)对P中单位元1,有1α=α(α∈V).
(6)对任意k,l∈P,α∈V有(kl)α=k(lα).
(7)对任意k,l∈P,α∈V有(k+l)α=kα+lα.
(8)对任意k∈P,α,β∈V有k(α+β)=kα+kβ.
则称V为域P上的一个线性空间,或向量空间。
其中,V中元素称为向量,V的零元称为零向量,P称为线性空间的基域。
当P是实数域时,V称为实线性空间;当P是复数域时,V称为复线性空间。
1.3 运算
1.3.1 加 & 减
任意阶张量均可与自身形状相同的张量相加减。若与单一数字相加减,将为张量内所有元素加减对应数字(等同于张量与由对应数字组成、与其形状、大小相同的张量相加减)
标量:
# 标量
a = torch.tensor(1)
b = torch.tensor(2)
a + b, a + 1

向量:
# 向量
e = torch.tensor([1, 2, 3])
f = torch.tensor([2, 3, 4])
e + f, e + 1

矩阵:
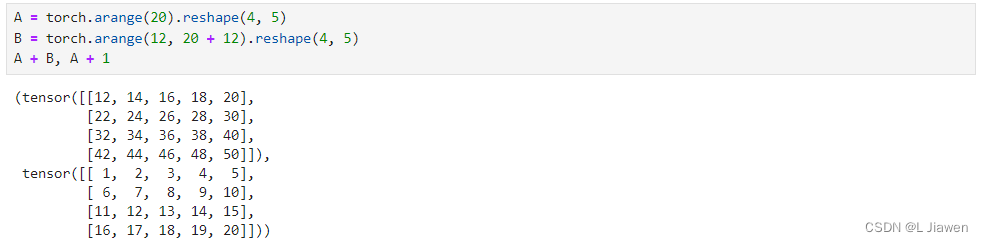
# 矩阵
A = torch.arange(20).reshape(4, 5)
B = torch.arange(12, 20 + 12).reshape(4, 5)
A + B, A + 1
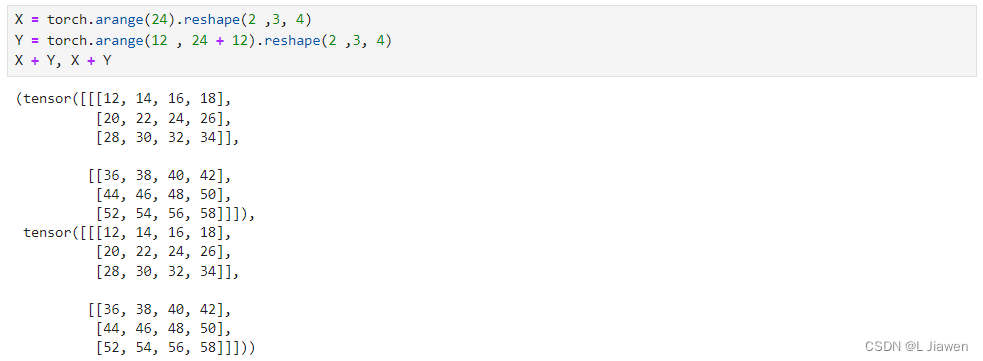
高阶张量:
# 高阶张量
X = torch.arange(24).reshape(2 ,3, 4)
Y = torch.arange(12 , 24 + 12).reshape(2 ,3, 4)
X + Y, X + Y
1.3.2 内积 & 点积
1.3.2.1 内积
内积(Inner Product): 亦称数量积(dot product; scalar product),是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。
假设有两向量
a
\boldsymbol{a}
a,
b
\boldsymbol{b}
b,则其内积表示如下:
⟨
a
,
b
⟩
\langle \boldsymbol{a}, \boldsymbol{b} \rangle
⟨a,b⟩
除此之外,还有 内积空间 的定义,有兴趣的读者可以自行查阅资料了解,这里不过多叙述。
计算向量内积的代码如下:
a = torch.tensor([1., 2., 3.])
b = torch.tensor([4., 5., 6.])
a.inner(b)

1.3.2.1 点积
点积(Dot Product):内积的一种特殊形式,即欧几里得空间内积的定义。
假设有两向量
a
\boldsymbol{a}
a,
b
\boldsymbol{b}
b,则其点积表示如下:
a
⋅
b
=
a
1
∗
b
1
+
a
2
∗
b
2
+
⋯
+
a
n
∗
b
n
=
∑
i
=
1
n
a
i
∗
b
i
\boldsymbol{a} \cdot \boldsymbol{b} = a_1 * b_1 + a_2 * b_2 + \cdots + a_n * b_n = \sum_{i=1}^{n}a_i * b_i
a⋅b=a1∗b1+a2∗b2+⋯+an∗bn=i=1∑nai∗bi
计算向量点积的代码如下:
a = torch.tensor([1., 2., 3.])
b = torch.tensor([4., 5., 6.])
a.dot(b)

1.3.3 外积 & 克罗内克积
克罗内克积(Kronecker product):张量积的特殊形式
- 克罗内克积是两个任意大小的矩阵间的运算,结果仍为一个矩阵(数学符号 ⊗ \otimes ⊗,精确表达 ⊗ k \otimes_{k} ⊗k)
我们以矩阵为例,用数学符号表示其计算过程:
A
m
×
n
⊗
B
p
×
q
=
[
a
11
B
⋯
a
m
1
B
⋮
⋱
⋮
a
1
n
B
⋯
a
m
n
B
]
=
[
a
11
b
11
a
11
b
12
⋯
a
11
b
1
q
⋯
⋯
a
1
n
b
11
a
1
n
b
12
⋯
a
1
n
b
1
q
a
11
b
11
a
11
b
12
⋯
a
11
b
1
q
⋯
⋯
a
1
n
b
11
a
1
n
b
12
⋯
a
1
n
b
1
q
⋮
⋮
⋱
⋮
⋮
⋮
⋱
⋮
a
11
b
p
1
a
11
b
p
2
⋯
a
11
b
p
q
⋯
⋯
a
1
n
b
p
1
a
1
n
b
p
2
⋯
a
1
n
b
p
q
⋮
⋮
⋱
⋮
⋱
⋮
⋮
⋮
⋮
⋮
⋱
⋮
⋱
⋮
⋮
⋮
a
m
1
b
11
a
m
1
b
12
⋯
a
m
1
b
1
q
⋯
⋯
a
m
n
b
11
a
m
n
b
12
⋯
a
m
n
b
1
q
a
m
1
b
21
a
m
1
b
22
⋯
a
m
1
b
2
q
⋯
⋯
a
m
n
b
21
a
m
n
b
22
⋯
a
m
n
b
2
q
⋮
⋮
⋱
⋮
⋮
⋮
⋱
⋮
a
m
1
b
p
1
a
m
1
b
p
2
⋯
a
m
1
b
p
q
⋯
⋯
a
m
n
b
p
1
a
m
n
b
p
2
⋯
a
m
n
b
p
q
]
A_{m×n} \otimes B_{p×q} = \begin{bmatrix} a_{11}B & \cdots & a_{m1}B \\ \vdots & \ddots & \vdots \\ a_{1n}B & \cdots & a_{mn}B \end{bmatrix} = \begin{bmatrix} a_{11}b_{11} & a_{11}b_{12} & \cdots & a_{11}b_{1q}& \cdots & \cdots & a_{1n}b_{11} & a_{1n}b_{12} & \cdots & a_{1n}b_{1q} \\ a_{11}b_{11} & a_{11}b_{12} & \cdots & a_{11}b_{1q}& \cdots & \cdots & a_{1n}b_{11} & a_{1n}b_{12} & \cdots & a_{1n}b_{1q} \\ \vdots & \vdots & \ddots & \vdots & & & \vdots & \vdots & \ddots & \vdots \\ a_{11}b_{p1} & a_{11}b_{p2} & \cdots & a_{11}b_{pq}& \cdots & \cdots & a_{1n}b_{p1} & a_{1n}b_{p2} & \cdots & a_{1n}b_{pq} \\ \vdots & \vdots & \ddots & \vdots & \ddots & & \vdots & \vdots & & \vdots \\ \vdots & \vdots & \ddots & \vdots & & \ddots & \vdots & \vdots & & \vdots \\ a_{m1}b_{11} & a_{m1}b_{12} & \cdots & a_{m1}b_{1q}& \cdots & \cdots & a_{mn}b_{11} & a_{mn}b_{12} & \cdots & a_{mn}b_{1q} \\ a_{m1}b_{21} & a_{m1}b_{22} & \cdots & a_{m1}b_{2q}& \cdots & \cdots & a_{mn}b_{21} & a_{mn}b_{22} & \cdots & a_{mn}b_{2q} \\ \vdots & \vdots & \ddots & \vdots & & & \vdots & \vdots & \ddots & \vdots \\ a_{m1}b_{p1} & a_{m1}b_{p2} & \cdots & a_{m1}b_{pq}& \cdots & \cdots & a_{mn}b_{p1} & a_{mn}b_{p2} & \cdots & a_{mn}b_{pq} \\ \end{bmatrix}
Am×n⊗Bp×q=
a11B⋮a1nB⋯⋱⋯am1B⋮amnB
=
a11b11a11b11⋮a11bp1⋮⋮am1b11am1b21⋮am1bp1a11b12a11b12⋮a11bp2⋮⋮am1b12am1b22⋮am1bp2⋯⋯⋱⋯⋱⋱⋯⋯⋱⋯a11b1qa11b1q⋮a11bpq⋮⋮am1b1qam1b2q⋮am1bpq⋯⋯⋯⋱⋯⋯⋯⋯⋯⋯⋱⋯⋯⋯a1nb11a1nb11⋮a1nbp1⋮⋮amnb11amnb21⋮amnbp1a1nb12a1nb12⋮a1nbp2⋮⋮amnb12amnb22⋮amnbp2⋯⋯⋱⋯⋯⋯⋱⋯a1nb1qa1nb1q⋮a1nbpq⋮⋮amnb1qamnb2q⋮amnbpq
下面我们分别展示求标量、向量、矩阵、高阶张量的克罗内克积。
标量-克罗内克积:
a = torch.tensor([2])
b = torch.tensor([3])
a.kron(b)

向量-克罗内克积:
x = torch.arange(3)
y = torch.arange(2, 2 + 3)
x.kron(y)

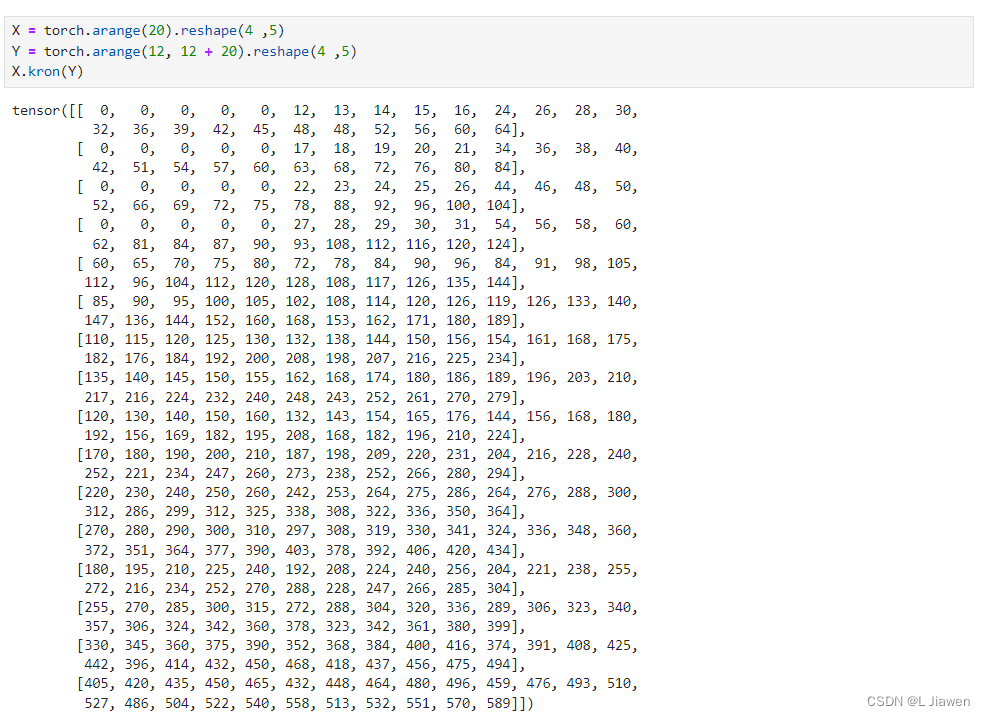
矩阵-克罗内克积:
X = torch.arange(20).reshape(4 ,5)
Y = torch.arange(12, 12 + 20).reshape(4 ,5)
X.kron(Y)
高阶张量-克罗内克积:
U = torch.arange(24).reshape(2, 3, 4)
V = torch.arange(15, 15 + 24).reshape(2, 3, 4)
U.kron(V)

1.3.4 哈达玛积
两个张量(标量、向量、矩阵、高阶张量)的按元素乘法称为哈达玛积(Hadamard Product)(数学符号
⊙
\odot
⊙),在代码中用*表示求哈达玛积。
我们以矩阵为例,用数学符号表示其计算过程:
A ⊙ B = [ a 11 a 21 ⋯ a m 1 a 12 a 22 ⋯ a m 2 ⋮ ⋮ ⋱ ⋮ a 1 n a 2 n ⋯ a m n ] ⊙ [ b 11 b 21 ⋯ b m 1 b 12 b 22 ⋯ b m 2 ⋮ ⋮ ⋱ ⋮ b 1 n b 2 n ⋯ b m n ] = [ a 11 ∗ b 11 a 21 ∗ b 21 ⋯ a m 1 ∗ b m 1 a 12 ∗ b 12 a 22 ∗ b 22 ⋯ a m 2 ∗ b m 2 ⋮ ⋮ ⋱ ⋮ a 1 n ∗ b 1 n a 2 n ∗ b 2 n ⋯ a m n ∗ b m n ] A \odot B = \begin{bmatrix} a_{11} & a_{21} & \cdots & a_{m1} \\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \end{bmatrix} \odot \begin{bmatrix} b_{11} & b_{21} & \cdots & b_{m1} \\ b_{12} & b_{22} & \cdots & b_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ b_{1n} & b_{2n} & \cdots & b_{mn} \end{bmatrix} =\begin{bmatrix} a_{11} * b_{11} & a_{21} * b_{21} & \cdots & a_{m1} * b_{m1} \\ a_{12} * b_{12} & a_{22} * b_{22} & \cdots & a_{m2} * b_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} * b_{1n} & a_{2n} * b_{2n} & \cdots & a_{mn} * b_{mn} \end{bmatrix} A⊙B= a11a12⋮a1na21a22⋮a2n⋯⋯⋱⋯am1am2⋮amn ⊙ b11b12⋮b1nb21b22⋮b2n⋯⋯⋱⋯bm1bm2⋮bmn = a11∗b11a12∗b12⋮a1n∗b1na21∗b21a22∗b22⋮a2n∗b2n⋯⋯⋱⋯am1∗bm1am2∗bm2⋮amn∗bmn
下面我们分别展示求标量、向量、矩阵、高阶张量的哈达玛积。
标量-哈达玛积:
a = torch.tensor([2])
b = torch.tensor([3])
a * b

向量-哈达玛积:
x = torch.arange(3)
y = torch.arange(2, 2 + 3)
x * y

矩阵-哈达玛积:
X = torch.arange(20).reshape(4 ,5)
Y = torch.arange(12, 12 + 20).reshape(4 ,5)
X * Y

高阶张量-哈达玛积:
U = torch.arange(24).reshape(2, 3, 4)
V = torch.arange(15, 15 + 24).reshape(2, 3, 4)
U * V

1.3.5 矩阵乘积
矩阵乘积(Matrix Product):
A
m
×
n
⋅
B
n
×
p
=
C
m
×
p
A_{m×n}·B_{n×p}=C_{m×p}
Am×n⋅Bn×p=Cm×p,即A的列数须与B的行数相等,
C
i
,
j
=
∑
k
=
1
n
A
i
,
k
B
k
,
j
C_{i,j}=\sum_{k=1}^{n}A_{i,k}B_{k,j}
Ci,j=∑k=1nAi,kBk,j,在代码中用符号@表示。
标量-标量 矩阵乘积 :标量与标量乘积可用符号@表示,也可用torch.matmul()运算。
c = torch.tensor([2])
d = torch.tensor([3])
c @ d

向量-矩阵 矩阵乘积 :
向量与矩阵乘积可用符号@表示,也可用torch.mv()或torch.matmul()运算。
区别:
torch.mv()须确保矩阵为第一个参数,向量为第二个参数,且形状符合运算规则。@或torch.matmul()则无上述限制,可将两者视为普通矩阵进行运算。
e = torch.arange(4.) # 等效于 torch.arange(4.0)
f = torch.arange(5.)
B = torch.arange(12.,20+12).reshape(4,5)
e @ B, e.matmul(B), B.mv(f)

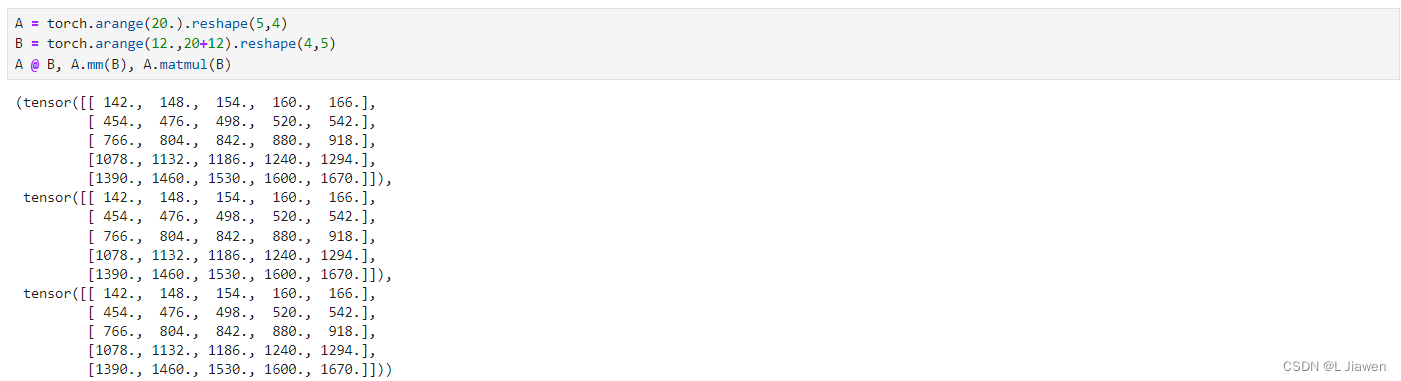
矩阵-矩阵 矩阵乘积 :
向量与矩阵乘积可用符号@表示,也可用torch.mm()或torch.matmul()运算。
A = torch.arange(20.).reshape(5,4)
B = torch.arange(12.,20+12).reshape(4,5)
A @ B, A.mm(B), A.matmul(B)
1.3.6 向量-向量叉积
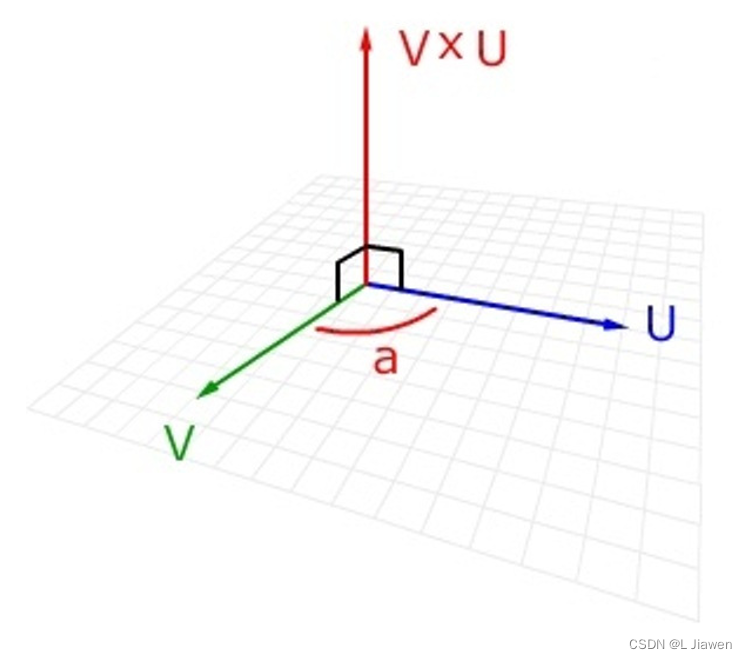
向量积(Cross Product),又称叉积,是一种在向量空间中向量的二元运算,其可以新产生一个与原两向量都垂直的向量。
可以用数学符号 × × ×表示叉积,有时也用^表示叉积避免与字母 x x x混淆。
向量积:|c|=|a×b|=|a||b|sin<a,b>
即c的长度在数值上等于以a,b,夹角为θ组成的平行四边形的面积。
而c的方向垂直于a与b所决定的平面,c的指向按右手定则从a转向b来确定。(一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的:若坐标系是满足右手定则的,当右手的四指从a以不超过180度的转角转向b时,竖起的大拇指指向是c的方向。)
在PyTorch中求两向量叉积的方式如下。
x = torch.tensor([1, 2, 3])
y = torch.tensor([4, 5, 6])
x.cross(y)

1.4 范数
PyTorch范数API
torch.norm(input, p='fro', dim=None, keepdim=False, out=None, dtype=None)
其中,参数释义如下:
- input:输入tensor类型的数据(张量内元素须为浮点型/复数)
- p指定的范数
- ‘fro’:Frobenius范数,即矩阵各项元素的绝对值平方总和。
- ‘nuc’:核范数,即矩阵奇异值之和。
- int型:p范数。
- dim:指定计算维度,默认所有维度计算。
- keepdim:布尔型,决定是否保留dim指定维度。
- out:输出的tensor。
- dtype:指定输出的tensor的数据类型。
首先我们定义所需的向量、矩阵。
x = torch.tensor([1., 2., 3.]) # 数字加小数点创建,默认为double型
y = torch.tensor([4., 5., 6.])
"""另外两种创建方式及不同浮点类型"""
# x = torch.tensor([1, 2, 3], dtype = torch.float64) # 指定float64
# y = torch.tensor([4, 5, 6], dtype = torch.float64)
# x = torch.FloatTensor([1, 2, 3]) # 此方式默认float32
# y = torch.FloatTensor([4, 5, 6])
A = torch.arange(12, dtype = torch.double).reshape(3, 4)
B = torch.arange(20, dtype = torch.double).reshape(4, 5)
1.4.1 向量范数(p范数)
1.4.1.1 l 1 \mathscr{l_1} l1范数
曼哈顿范数(L1范数):向量所有分量绝对值之和,它受异常值影响较小。
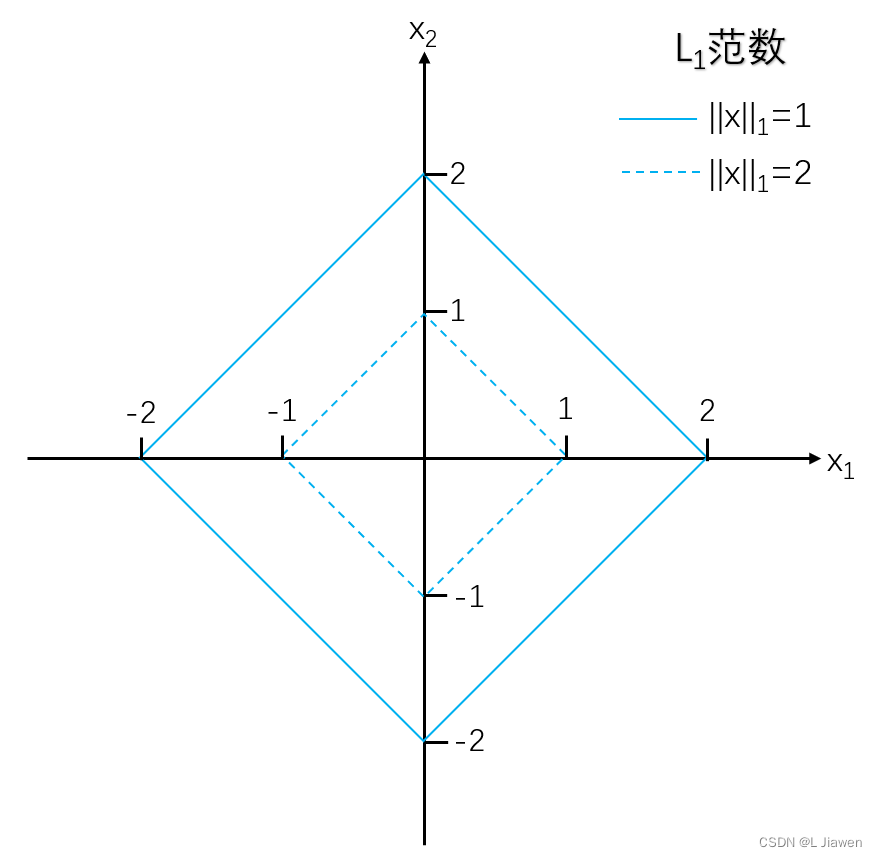
∣
∣
x
∣
∣
1
=
∑
i
=
1
n
∣
x
i
∣
||\boldsymbol{x}||_{1}=\sum_{i=1}^{n}|x_{i}|
∣∣x∣∣1=i=1∑n∣xi∣
代码如下:
x.norm(p=1)

1.4.1.2 l 2 \mathscr{l_2} l2范数
欧几里得范数(L2范数):向量所有分量绝对值平方和的平方根。
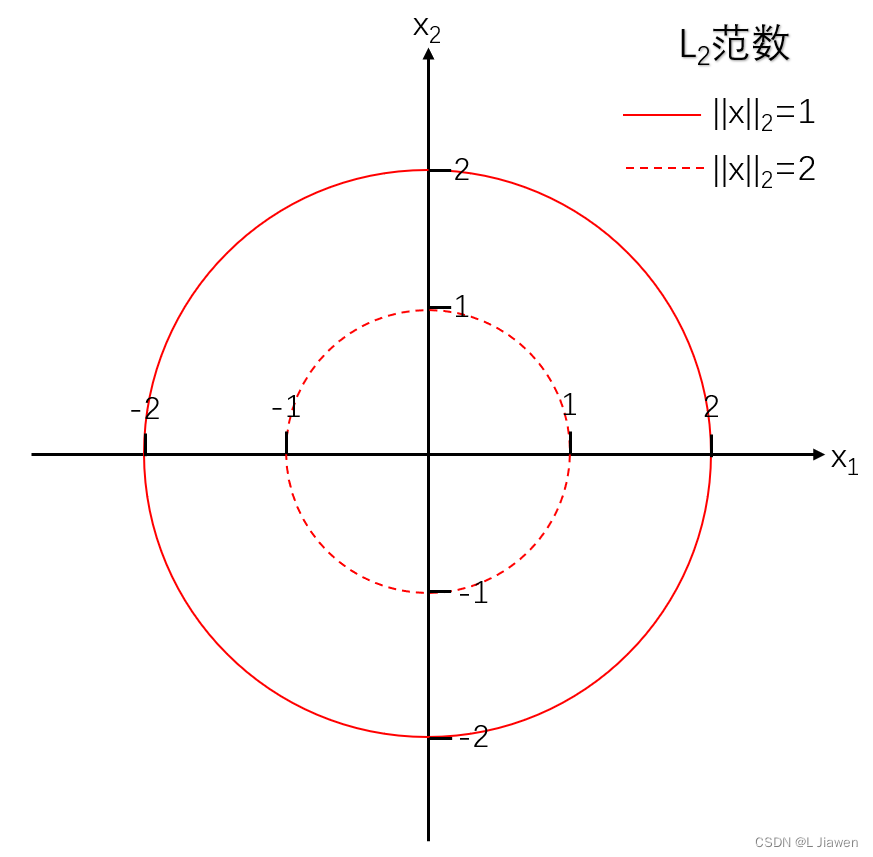
∣ ∣ x ∣ ∣ 2 = ∑ i = 1 n x i 2 = ( ∑ i = 1 n x i 2 ) 1 2 ||\boldsymbol{x}||_{2}=\sqrt{\sum_{i=1}^{n}x_{i}^{2}}=(\sum_{i=1}^{n}x_{i}^{2})^{\frac{1}{2}} ∣∣x∣∣2=i=1∑nxi2=(i=1∑nxi2)21
代码如下:
x.norm(p=2)

1.4.1.3 l ∞ \mathscr{l_\infty} l∞范数
切比雪夫范数(L∞范数):向量所有分量绝对值最大值。
∣ ∣ x ∣ ∣ ∞ = lim p → ∞ ∑ i = 1 n ∣ x i ∣ p p = lim p → ∞ ( ∑ i = 1 n ∣ x i ∣ p ) 1 p = max ( ∣ x i ∣ ) ||\boldsymbol{x}||_{\infty}=\lim_{p\to \infty}\sqrt[p]{\sum_{i=1}^{n}|x_{i}|^{p}}=\lim_{p\to \infty}(\sum_{i=1}^{n}|x_{i}|^{p})^{\frac{1}{p}}=\max(|x_{i}|) ∣∣x∣∣∞=p→∞limpi=1∑n∣xi∣p=p→∞lim(i=1∑n∣xi∣p)p1=max(∣xi∣)
我们已经发现了距离间的规律,这些范数被统称为p范数,可用如下公式表示所有向量p范数:
∣
∣
x
∣
∣
p
=
∑
i
=
1
n
∣
x
i
∣
p
p
=
(
∑
i
=
1
n
∣
x
i
∣
p
)
1
p
||\boldsymbol{x}||_{p}=\sqrt[p]{\sum_{i=1}^{n}|x_{i}|^{p}}=(\sum_{i=1}^{n}|x_{i}|^{p})^{\frac{1}{p}}
∣∣x∣∣p=pi=1∑n∣xi∣p=(i=1∑n∣xi∣p)p1
- 当 p = 1 时,上式表示 曼哈顿范数
- 当 p = 2 时,上式表示 欧几里得范数
- 当 p → ∞ 时,上式表示 切比雪夫范数
1.4.2 矩阵范数
1.4.2.1 F r o b e n i u s \mathscr{Frobenius} Frobenius范数
弗罗贝尼乌斯范数:类似于向量的L2范数,矩阵 X ∈ R m × n X\in\mathbb{R^{m×n}} X∈Rm×n的弗罗贝尼乌斯范数是矩阵元素平方和的平方根。
∣
∣
X
∣
∣
F
=
∑
i
=
1
m
∑
j
=
1
n
x
i
j
2
||X||_{F}=\sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n}x_{ij}^{2}}
∣∣X∣∣F=i=1∑mj=1∑nxij2
它具有向量范数的所有性质,代码如下:
# torch默认计算Frobenius范数
A.norm()

1.4.2.2 核范数
核范数:矩阵奇异值的和,可以用来衡量矩阵的稀疏性。我们可用核范数来约束模型的复杂度,防止过拟合。
∣ ∣ X ∣ ∣ ∗ = t r ( X T X ) = ∣ ∣ U ∣ ∣ 1 ||X||_{*} = tr(\sqrt{X^{T}X})=||U||_{1} ∣∣X∣∣∗=tr(XTX)=∣∣U∣∣1
其中,U是A的奇异值分解(SVD)的左奇异矩阵, ∣ ∣ U ∣ ∣ 1 ||U||_{1} ∣∣U∣∣1表示其L1范数,核范数非负。
该范数常被用于约束矩阵的低秩,对于稀疏性质的数据而言,其矩阵是低秩且会包含大量冗余信息,这些信息可被用于恢复数据和提取特征。
A.norm(p='nuc')

1.5 距离(向量距离)
PyTorch距离API
torch.pairwise_distance(x1, x2, p=2.0, eps=1e-6, keepdim=False)
其中,input表示输入,p表示距离类型(默认为l2距离)
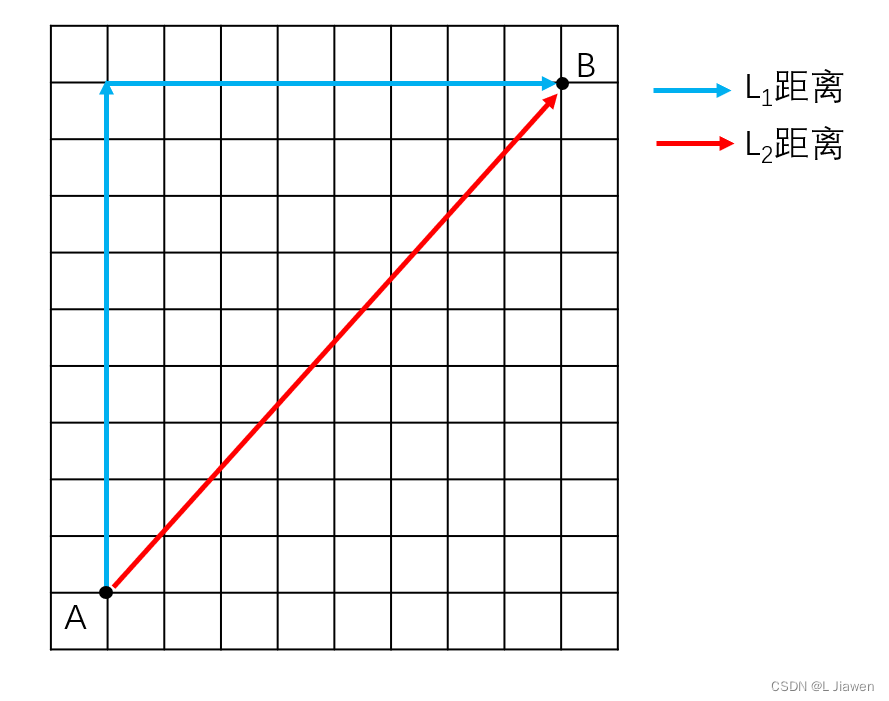
1.5.1 l 1 \mathscr{l_1} l1距离
曼哈顿距离(L1距离):在n维空间中,两点各坐标数值差绝对值之和。
d
1
=
∑
i
=
1
n
∣
x
i
−
y
i
∣
d_{1}=\sum_{i=1}^{n}|x_{i} - y_{i}|
d1=i=1∑n∣xi−yi∣
torch.pairwise_distance(x, y, p=1)

1.5.2 l 2 \mathscr{l_2} l2距离
欧几里得距离(L2距离):在n维空间中,两点各坐标数值差绝对值平方和的平方根。
d
2
=
∑
i
=
1
n
(
x
i
−
y
i
)
2
=
(
∑
i
=
1
n
x
i
2
−
y
i
)
2
)
1
2
d_{2}=\sqrt{\sum_{i=1}^{n}(x_{i} - y_{i})^{2}}=(\sum_{i=1}^{n}x_{i}^{2} - y_{i})^{2})^{\frac{1}{2}}
d2=i=1∑n(xi−yi)2=(i=1∑nxi2−yi)2)21
torch.pairwise_distance(x, y, p=2)

1.5.3 l ∞ \mathscr{l_\infty} l∞距离
切比雪夫距离(L∞距离):在n维空间中,两点各坐标数值差绝对值的最大值。
d
∞
=
lim
p
→
∞
∑
i
=
1
n
∣
x
i
−
y
i
∣
p
p
=
lim
p
→
∞
(
∑
i
=
1
n
∣
x
i
−
y
i
∣
p
)
1
p
=
max
(
∣
x
i
−
y
i
∣
)
d_{\infty}=\lim_{p\to \infty}\sqrt[p]{\sum_{i=1}^{n}|x_{i} - y_{i}|^{p}}=\lim_{p\to \infty}(\sum_{i=1}^{n}|x_{i} - y_{i}|^{p})^{\frac{1}{p}}=\max(|x_{i} - y_{i}|)
d∞=p→∞limpi=1∑n∣xi−yi∣p=p→∞lim(i=1∑n∣xi−yi∣p)p1=max(∣xi−yi∣)
我们已经发现了距离间的规律,可用如下公式表示所有向量距离:
d
p
=
∑
i
=
1
n
∣
x
i
−
y
i
∣
p
p
=
(
∑
i
=
1
n
∣
x
i
−
y
i
∣
p
)
1
p
d_{p}=\sqrt[p]{\sum_{i=1}^{n}|x_{i} - y_{i}|^{p}}=(\sum_{i=1}^{n}|x_{i} - y_{i}|^{p})^{\frac{1}{p}}
dp=pi=1∑n∣xi−yi∣p=(i=1∑n∣xi−yi∣p)p1
- 当 p = 1 时,上式表示 曼哈顿距离
- 当 p = 2 时,上式表示 欧几里得距离
- 当 p → ∞ 时,上式表示 切比雪夫距离
1.6 余弦相似度
余弦相似度:又称为余弦相似性,是通过计算两个向量的夹角余弦值来评估他们的相似度。
s i m i l a r i t y = c o s ( θ ) = a ⋅ b ∣ ∣ a ∣ ∣ ⋅ ∣ ∣ b ∣ ∣ = ∑ i = 1 n a i × b i ∑ i = 1 n ( a i ) 2 × ∑ i = 1 n ( b i ) 2 similarity=cos(\theta)=\frac{\boldsymbol{a}·\boldsymbol{b}}{||\boldsymbol{a}||·||\boldsymbol{b}||}=\frac{\sum_{i=1}^{n}a_{i}×b_{i}}{\sqrt{\sum_{i=1}^{n}(a_{i})^{2}}×\sqrt{\sum_{i=1}^{n}(b_{i})^{2}}} similarity=cos(θ)=∣∣a∣∣⋅∣∣b∣∣a⋅b=∑i=1n(ai)2×∑i=1n(bi)2∑i=1nai×bi
PyTorch余弦相似度API
torch.cosine_similarity(x1, x2, dim=1, eps=1e-8)
代码示例如下:
a = torch.tensor([1., 2, 3])
b = torch.tensor([2., 3, 4])
# 'Tensor' object has no attribute 'cosine_similarity'
# Tensor类型对象未内置cosine_similarity方法,需按如下方式调用
torch.cosine_similarity(a, b, dim=0)

1.7 矩阵分解
矩阵分解:将矩阵拆解为数个矩阵的乘积
1.7.1 矩阵三角分解(LR / LU分解)
三角分解:最常见的一种分解方式,便于我们求原矩阵的行列式、逆矩阵等。
1.7.2 矩阵正交三角分解(QR分解)
正交三角分解:矩阵先经过正交相似变化成为Hessenberg矩阵,再应用QR方法求特征值和特征向量。它是将矩阵分解成一个正规正交矩阵Q与上三角形矩阵R,所以称为QR分解法,与此正规正交矩阵的通用符号Q有关。
1.7.3 矩阵特征值分解(EVD分解)
特征值分解:亦称谱分解(Spectral Decomposition),将矩阵分解成特征值和特征向量表示的矩阵乘法的形式。
定义:
A
A
A是一个n×n方阵,且有n个线性无关的特征向量
q
i
(
i
=
1
,
.
.
.
,
n
)
q_{i}(i=1,...,n)
qi(i=1,...,n),可将
A
A
A分解为:
A
=
Q
Λ
Q
−
1
A=Q \Lambda Q^{-1}
A=QΛQ−1
其中,Q是n×n方针,且第i列为A的特征向量
q
i
q_{i}
qi。
Λ
\Lambda
Λ是对角矩阵,其对角线上的元素对应特征值,即
Λ
i
i
=
λ
i
\Lambda_{ii}=\lambda_{i}
Λii=λi。
只有可对角化矩阵(满秩)才能作特征分解。
1.7.4 矩阵奇异值分解(SVD分解)
定义:
A
A
A是一个m×n实矩阵,存在一个分解使得
A
=
U
Σ
V
T
A=U \Sigma V^{T}
A=UΣVT
其中,
U
U
U是m×m阶正交矩阵,$\Sigma
是
m
×
n
阶非负实数对角矩阵,
是m×n阶非负实数对角矩阵,
是m×n阶非负实数对角矩阵,V$是n×n阶正交矩阵。
奇异值分解使得非方阵也能进行分解,由于 A A T AA^{T} AAT必定为实对称矩阵,对它进行特征值分解,被称作对A进行奇异值分解。
其中, U U U和 V V V均为正交矩阵, Σ \Sigma Σ是对角矩阵,根据特征值分解可以得到具体说明如下:
- U U U被称为A的左奇异矩阵,其列组成的向量是方阵 A A T AA_{T} AAT的特征向量,亦称 A A A的左奇异向量。
- V V V被称为A的右奇异矩阵,其列组成的向量是方阵 A A T AA_{T} AAT的特征向量,亦称 A A A的右奇异向量。
- Σ \Sigma Σ对角线上的元素 σ i i \sigma_{ii} σii即为A的奇异值,它们等于 A A T AA_{T} AAT及 A T A A_{T}A ATA特征值的平方根( σ = λ \sigma=\sqrt{\lambda} σ=λ),行对应 U U U的列向量,列对应 V V V的列向量。
奇异值分解的代码如下:
A = torch.tensor([[1., 2., 3., 4.],[2., 3., 4., 5.],[3., 4., 5., 6.]])
A.svd()

1.8 降维
1.8.1 基础操作
1.8.1.1 求和
我们可对张量所有元素求和:
x = torch.arange(6, dtype=torch.double)
x, x.sum()

还可以指定按列/行元素求和:
A = torch.arange(20, dtype=torch.double).reshape(5, 4)
A_sum_axis0 = A.sum(axis=0) # 将矩阵列向量求和(沿着行挨个列向量求和)
A_sum_axis1 = A.sum(axis=1) # 将矩阵行向量求和(沿着列挨个行向量求和)
A_sum = A.sum(axis=[0, 1]) # 沿着行、列对矩阵求和,等价于对矩阵所有元素求和
A_sum_axis0, A_sum_axis1, A_sum

1.8.1.2 平均值
同样,我们可对张量所有元素求平均,也可以指定按列/行元素求平均:
A = torch.arange(20, dtype=torch.double).reshape(5, 4)
A_mean = A.mean() # 全部元素求平均
A_mean0 = A.mean(axis=0) # 将矩阵列向量求平均(沿着行挨个列向量求平均)
A_mean1 = A.mean(axis=1) # 将矩阵行向量求平均(沿着列挨个行向量求平均)
A_mean, A_mean0, A_mean1

1.8.2 PCA主成分分析
PCA(principal components analysis)主成分分析,亦称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标。
在统计学中,主成分分析PCA是一种简化数据集的技术。它是一个线性变换。这个变换把数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。主成分分析经常用于减少数据集的维数,同时保持数据集的对方差贡献最大的特征。
1.8.3 稀疏矩阵压缩
仅存储矩阵中的非0元素,同时存储该元素所在矩阵中的行标和列标。
其中常用的有:按列压缩(CSC, Compressed sparse column)、按行压缩(CSR, Compressed sparse row)等。
2. 微积分
在深度学习中,我们“训练模型”使其变得更好,即最小化一个损失函数(loss function)。
我们“训练”模型只能将模型与我们实际见到的数据相拟合,因此可将此任务分解为两个关键问题:
- 优化(optimization):用模型拟合观察数据的过程。
- 泛化(generalization):指导生成有效性超出用于训练的数据集本身的模型。
2.1 导数 & 微分
假设有一个函数
f
:
R
→
R
f:\mathbb{R}→\mathbb{R}
f:R→R,其输入和输出都是标量。若其导数存在,则极限被定义为:
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
f'(x) = \lim_{h→0} \frac{f(x+h)-f(x)}{h}
f′(x)=h→0limhf(x+h)−f(x)
若
f
′
(
a
)
f'(a)
f′(a)存在,则称f在a处可微(differentiable)
2.2 偏导数
在深度学习中,通常需要用到多变量,我们将其思想推广到多元函数(multivariate function)
设 y = f ( x 1 , x 2 , ⋯ , x n ) y = f(x_1,x_2,\cdots,x_n) y=f(x1,x2,⋯,xn),则y关于第i个参数x_i的偏导数(Partial Derivative)为:
∂ y ∂ x i = lim h → 0 f ( x 1 , ⋯ , x i − 1 , x i + h , x i + 1 , ⋯ , x n ) − f ( x 1 , ⋯ , x i , ⋯ , x n ) h \frac{\partial y}{\partial x_i}=\lim_{h→0} \frac{f(x_1, \cdots, x_{i-1}, x_i+h,x_{i+1},\cdots, x_n)-f(x_1,\cdots,x_i,\cdots,x_n)}{h} ∂xi∂y=h→0limhf(x1,⋯,xi−1,xi+h,xi+1,⋯,xn)−f(x1,⋯,xi,⋯,xn)
2.3 梯度
假设有一个函数
f
:
R
n
→
R
f:\mathbb{R^n}→\mathbb{R}
f:Rn→R,其输入是一个n维向量
x
=
[
x
1
,
x
2
,
⋯
,
x
n
]
\boldsymbol{x}=[x_1, x_2, \cdots, x_n]
x=[x1,x2,⋯,xn],其输出是一个标量,则函数
f
(
x
)
f(\boldsymbol{x})
f(x)相对于
x
\boldsymbol{x}
x的梯度是一个包含n个偏导数的向量:
∇
x
f
(
x
)
=
[
∂
f
(
x
)
∂
x
1
,
∂
f
(
x
)
∂
x
2
,
⋯
,
∂
f
(
x
)
∂
x
n
]
\nabla_{x}f(\boldsymbol{x})=[\frac{\partial f(\boldsymbol{x})}{\partial x_1},\frac{\partial f(\boldsymbol{x})}{\partial x_2},\cdots,\frac{\partial f(\boldsymbol{x})}{\partial x_n}]
∇xf(x)=[∂x1∂f(x),∂x2∂f(x),⋯,∂xn∂f(x)]
假设 x \boldsymbol{x} x为n维向量,在对多元函数求微分时经常使用以下规则:
- 对于所有 A ∈ R m × n A \in \mathbb{R}^{m×n} A∈Rm×n,都有 ∇ x A x = A T \nabla_{x}Ax=A^{T} ∇xAx=AT
- 对于所有 A ∈ R n × m A \in \mathbb{R}^{n×m} A∈Rn×m,都有 ∇ x x T A = A \nabla_{x}x^{T}A=A ∇xxTA=A
- 对于所有 A ∈ R n × n A \in \mathbb{R}^{n×n} A∈Rn×n,都有 ∇ x x T A x = ( A + A T ) x \nabla_{x}x^{T}Ax=(A+A^{T})x ∇xxTAx=(A+AT)x
- ∇ x ∣ ∣ x ∣ ∣ 2 = ∇ x x T x = 2 x \nabla_{x}||\boldsymbol{x}||^{2}=\nabla_{x}\boldsymbol{x}^{T}\boldsymbol{x}=2\boldsymbol{x} ∇x∣∣x∣∣2=∇xxTx=2x
同样,对于任何矩阵 X X X,都有 ∇ X ∣ ∣ X ∣ ∣ F 2 = 2 X \nabla_{X}||X||_{F}^2=2X ∇X∣∣X∣∣F2=2X。
例如,定义一个函数:
f
(
x
)
=
k
T
x
+
b
f(\boldsymbol{x})=\boldsymbol{k^{T}x} + \boldsymbol{b}
f(x)=kTx+b
其中:
k
T
=
[
1
,
3
,
5
]
b
T
=
[
1
,
2
,
3
]
k^{T}=[1,3,5] \\ b^{T}=[1,2,3]
kT=[1,3,5]bT=[1,2,3]
我们可采用自动微分的方式对示例这种函数求梯度,具体可参考下面两例。
2.4 Hessian矩阵
Hessian矩阵,中文译名为海森矩阵。
假设有一个函数
f
:
R
n
→
R
f:\mathbb{R^n}→\mathbb{R}
f:Rn→R,其Hessian矩阵定义如下:
H
(
f
)
=
[
∂
2
f
∂
x
1
2
∂
2
f
∂
x
1
∂
x
2
⋯
∂
2
f
∂
x
1
∂
x
n
∂
2
f
∂
x
2
∂
x
1
∂
2
f
∂
x
2
2
⋯
∂
2
f
∂
x
2
∂
x
n
⋮
⋮
⋱
⋮
∂
2
f
∂
x
n
∂
x
1
∂
2
f
∂
x
n
∂
x
2
⋯
∂
2
f
∂
x
n
2
]
H(f)= \begin{bmatrix} \frac{\partial^{2} f}{\partial x_1^{2}} & \frac{\partial^{2} f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^{2} f}{\partial x_1 \partial x_n} \\ \frac{\partial^{2} f}{\partial x_2 \partial x_1} & \frac{\partial^{2} f}{\partial x_2^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_n \partial x_1} & \frac{\partial^{2} f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^{2} f}{\partial x_n^{2}} \end{bmatrix}
H(f)=
∂x12∂2f∂x2∂x1∂2f⋮∂xn∂x1∂2f∂x1∂x2∂2f∂x22∂2f⋮∂xn∂x2∂2f⋯⋯⋱⋯∂x1∂xn∂2f∂x2∂xn∂2f⋮∂xn2∂2f
- 当H为正定矩阵时,则该点是极小值点
- 当H为负定矩阵时,则该点是极大值点
- 当H为不定矩阵时,则该点是非极值点
- 当H为半正定矩阵/半负定矩阵时, f ( x 1 , x 2 , ⋯ , x n ) f(x_1,x_2,\cdots,x_n) f(x1,x2,⋯,xn)则该点是 “可疑”极值点,需结合其他方法判定。
定义一个函数:
f
(
x
)
=
b
T
x
+
1
2
x
T
A
x
f(\boldsymbol{x})=\boldsymbol{b^{T}x}+\frac{1}{2} \boldsymbol{x^{T}Ax}
f(x)=bTx+21xTAx
其中:
b
T
=
[
1
,
3
,
5
]
A
=
[
−
5
−
3
−
0.5
−
3
−
2
0
−
0.5
0
−
0.5
]
b^{T}=[1,3,5] \\ A = \begin{bmatrix} -5 & -3 & -0.5 \\ -3 & -2 & 0 \\ -0.5 & 0 & -0.5 \end{bmatrix}
bT=[1,3,5]A=
−5−3−0.5−3−20−0.50−0.5
本例代码采用自动微分的方式,对上述函数对上述函数原点处的Hessian矩阵进行计算:
import torch
# 函数定义
x = torch.tensor([0., 0, 0], requires_grad=True)
b = torch.tensor([1., 3, 5])
A = torch.tensor([[-5, -3, -0.5],[-3, -2, 0],[-0.5, 0, -0.5]])
def func(x):
return b @ x + 0.5 * x @ A @ x
"""两次梯度求解Hessian矩阵"""
# 计算一阶导数,因为我们需要继续计算二阶导数,所以创建并保留计算图
grad = torch.autograd.grad(func(x), x, retain_graph=True, create_graph=True)
# 定义Print数组,为输出和进一步利用Hessian矩阵作准备
p = torch.tensor([])
for anygrad in grad[0]: # torch.autograd.grad返回的是元组
p = torch.cat((p, torch.autograd.grad(anygrad, x, retain_graph=True)[0]))
print(p.view(x.size()[0], -1))
"""API求解Hessian矩阵"""
print(torch.autograd.functional.hessian(func, x))

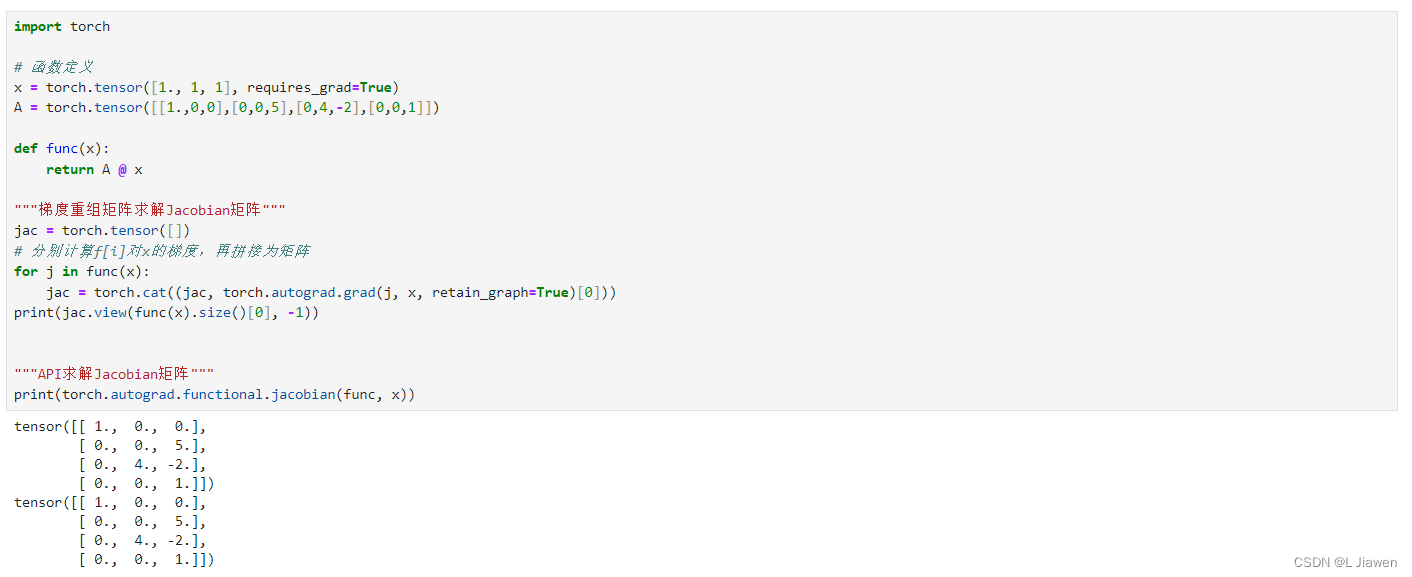
2.5 Jacobian矩阵
Jacobian矩阵,中文译名为雅可比矩阵。
假设有一个函数
f
:
R
n
→
R
m
\boldsymbol{f}:\mathbb{R^n}→\mathbb{R^m}
f:Rn→Rm,其由多个函数组成:
f
=
[
f
1
(
x
1
,
x
2
,
⋯
,
x
n
)
f
2
(
x
1
,
x
2
,
⋯
,
x
n
)
⋮
f
m
(
x
1
,
x
2
,
⋯
,
x
n
)
]
\boldsymbol{f} = \begin{bmatrix} f_{1}(x_1, x_2, \cdots, x_n)\\ f_{2}(x_1, x_2, \cdots, x_n)\\ \vdots \\ f_{m}(x_1, x_2, \cdots, x_n)\\ \end{bmatrix}
f=
f1(x1,x2,⋯,xn)f2(x1,x2,⋯,xn)⋮fm(x1,x2,⋯,xn)
其雅可比矩阵定义为:
J
(
f
)
=
[
∂
f
1
∂
x
1
∂
f
1
∂
x
2
⋯
∂
f
1
∂
x
n
∂
f
2
∂
x
1
∂
f
2
∂
x
2
⋯
∂
f
2
∂
x
n
⋮
⋮
⋱
⋮
∂
f
n
∂
x
1
∂
f
n
∂
x
2
⋯
∂
f
n
∂
x
n
]
J(\boldsymbol{f}) = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & \cdots & \frac{\partial f_n}{\partial x_n} \end{bmatrix}
J(f)=
∂x1∂f1∂x1∂f2⋮∂x1∂fn∂x2∂f1∂x2∂f2⋮∂x2∂fn⋯⋯⋱⋯∂xn∂f1∂xn∂f2⋮∂xn∂fn
定义一个函数( f : R 3 → R 4 \boldsymbol{f}:\mathbb{R^3}→\mathbb{R^4} f:R3→R4):
f ( x ) = [ f 1 ( x 1 , x 2 , x 3 ) f 2 ( x 1 , x 2 , x 3 ) f 3 ( x 1 , x 2 , x 3 ) f 4 ( x 1 , x 2 , x 3 ) ] = [ x 1 5 x 3 4 x 2 − 2 x 3 x 3 ] \boldsymbol{f}(\boldsymbol{x})=\begin{bmatrix} f_{1}(x_1,x_2,x_3) \\ f_{2}(x_1,x_2,x_3) \\ f_{3}(x_1,x_2,x_3) \\ f_{4}(x_1,x_2,x_3) \\ \end{bmatrix} =\begin{bmatrix} x_1 \\ 5x_3 \\ 4x_2-2x_3 \\ x_3 \\ \end{bmatrix} f(x)= f1(x1,x2,x3)f2(x1,x2,x3)f3(x1,x2,x3)f4(x1,x2,x3) = x15x34x2−2x3x3
import torch
# 函数定义
x = torch.tensor([1., 1, 1], requires_grad=True)
A = torch.tensor([[1.,0,0],[0,0,5],[0,4,-2],[0,0,1]])
def func(x):
return A @ x
"""梯度重组矩阵求解Jacobian矩阵"""
jac = torch.tensor([])
# 分别计算f[i]对x的梯度,再拼接为矩阵
for j in func(x):
jac = torch.cat((jac, torch.autograd.grad(j, x, retain_graph=True)[0]))
print(jac.view(func(x).size()[0], -1))
"""API求解Jacobian矩阵"""
print(torch.autograd.functional.jacobian(func, x))