目录
参考文献
问题
解法与证明
易读版本
-
参考文献
- Dijkstra于1965年发表文章Solution of a Problem in Concurrent Programming Control,引出并发系统下的互斥(mutual exclusion)问题,自此开辟了分布式计算领域
- Dijkstra在文中给出了基于共享存储原子性访问的解决方案只有十多行代码,但阅读起来较难以理解
- 在查阅若干资料后,总结了一种较为直观的解释方法
-
问题
- 考虑N个节点(进程),每个都在运行一个无限循环的程序
- 每轮循环当中都存在一个临界区(critical section)
- 我们需要设计算法控制多个计算机中,同时只有一台可以进入其临界区,并需要满足下列条件:
- 1-所有的节点是对称(symmetrical)的,即我们不能引入类似于“1号节点优先于2号节点”的静态优先级配置
- 2-各个节点的运行速度可能不同,同一个节点在不同时刻的运行速度也可能不同
- 3-任意节点在临界区外停止运行,不应引起系统的死锁
- 4-如果多个节点想要访问临界区,必须在有限时间内决策出哪个节点优先访问
- 各个节点之间可以通过共享存储(common store)通信,共享存储提供以字(word)为单位的原子性读写
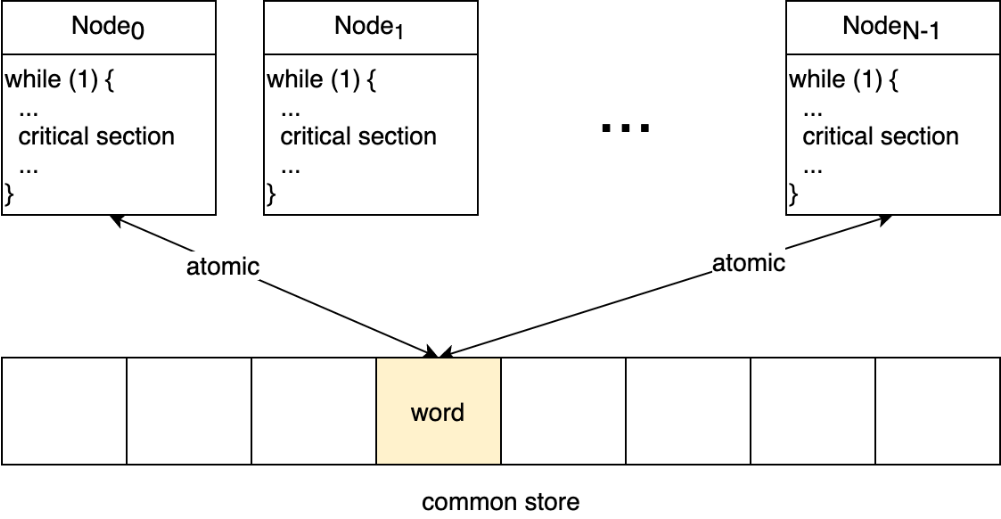
- 当今现在,在基于共享内存通信的单机多进程上,我们可以很方便的使用基于TAS(Test&Set)或CAS(Copy&Swap)实现的互斥锁mutex来实现临界区互斥访问
- 然而,在只有对内存单元原子读写的条件下,如何完成互斥访问呢?
- Dijkstra给出了他的解法
-
解法与证明
- 在共享存储上,Dijkstra使用了两个长度为N的布尔数组,和一个整数:

- 其中,k 满足 1⩽k⩽N,b[i] 和 c[i] 只被节点 i 修改,且初始值为true
- 对于第 i 个节点(1⩽i⩽N),执行下面的代码:

- Dijkstra原文中给出的证明集中论证两点:
- 第一,所有节点互斥访问临界区
- 第二,不会出现系统死锁
- 建议大家可以先结合代码看下原文中证明
-
易读版本
- 在此,为了便于理解,对原代码做了如下修改:
- 修改为c语言版本
- 将数组和节点下标修改为通用的 0,1,…,N−1
- 将数组 b 改名为 want_to_enter_critical_section(希望进入临界区),数组 c 改名为 in_critical_section(在临界区)
- 将 b 和 c 数组的初始值改为 false ,并翻转代码中所有的布尔值,即 false 改为 true,true 改为 false

- 证明:
- 1. mutual exclusion(互斥)
- 如果程序想运行到critical section,则必须运行通过 Li4 中的代码且不返回 Li1
- 即,除了自身的 in_critical_section[i] 为 true 外,其余所有节点的 in_critical_section[i] 均为 false
- 2. non-blocking(非阻塞)
- 如果第 k 个节点不在 Li0~Li4 的循环中,则 want_to_enter_critical_section 为 false
- 所有在循环中的节点会在 Li1 判定 (k != i),其中的一个或多个节点会执行到 Li3 ,其中某个节点将设定 k = i
- 此后 want_to_enter_critical_section[k] 为 true,其他节点无法再更改 k ,直至离开critical section后将 want_to_enter_critical_section[k] 为 false
- 在 k 被确定后,第k个节点会不断尝试 Li4 中的代码,直至其余所有的 in_critical_section[i] 全部为 false
- 这种情况必然会发生,不论临界区中的节点离开临界区,还是临界区外的发现 Li1: k != i,都会执行 in_critical_section[i] = false;
- 证毕
- 1. mutual exclusion(互斥)
- 并发情况
- 这里Dijstra原文中没有明确指出的是,考虑并发情况下两个节点 x 和 y 同时运行 Li4 中代码,则会出现下面的情况
- 此种情况下,两个节点都 goto Li1
- x 和 y 中不等于 k 的节点会执行 Li2,从而使得节点 k 在下次执行 Li4 时成功通过,进入临界区