本篇根据十大经典排序算法-堆排序算法详解进行整理和补充。

1. 基础知识点

1.1 完全二叉树

之前在介绍二叉树时讲过一个完全二叉树，具体参考C++数据结构X篇_13_二叉树基本概念、性质及表示法，其中介绍到的完全二叉树，下图即为一个完全二叉树。

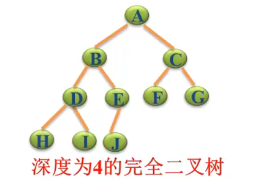
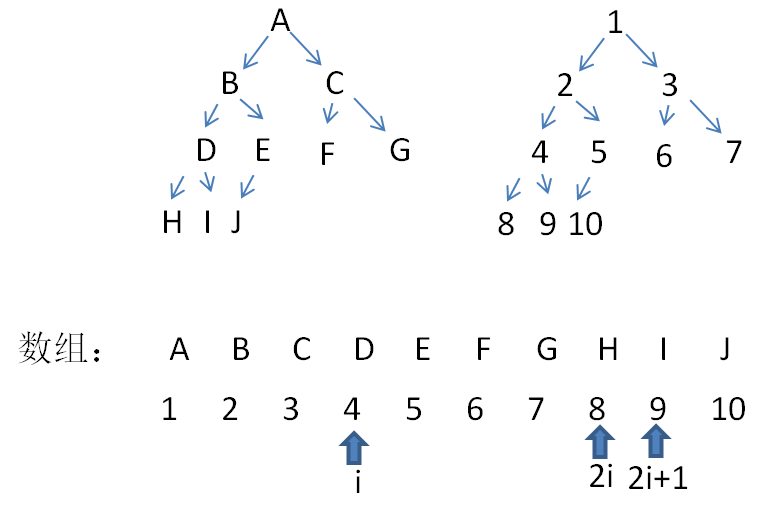
可以看到从A–G是一个满二叉树，最后一层靠左，完全二叉树可以按照从上往下，从左往右将A–J存到数组中，将A–J假设为1-10的数(可以认为是下标)，D对应数字4的左子树为24=8，对应的D的右子树为24+1，在A–J数组中去看，D的下标为4，左右子树值为8和9。从上可以看出，完全二叉树可以存储到数组中，同时保持其节点关系。

任意非叶子结点，左子树2i，右子树2i+1.

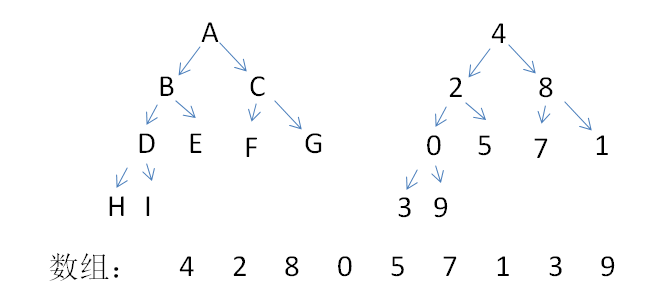
如果将乱序的数给到完全二叉树中，就变成如下图所示的结构：

1.2 堆的基础知识

什么是堆呢？
堆的性质：

• 堆是一颗完全二叉树

• 堆是一种重要的数据结构，堆分为大根堆和小根堆，大根堆堆顶的数据是最大的，小根堆堆顶的数据是最小的，堆在逻辑结构上是一颗完全二叉树，这棵树中如果满足根节点大于左右子树，每个节点都满足这个条件就是大根堆，反之就是小根堆。（这里的大和小并不是传统意义下的大和小，它是相对于优先级而言的）
  常用操作中，堆的插入就是把新的元素放到堆底，然后检查它是否符合堆的性质，如果符合就丢在那里了，如果不符合，那就和它的父亲交换一下，一直交换交换交换，直到符合堆的性质，那么就插入完成了

• 父结点比其子结点都大，最大的数在最上面，称为大顶堆

• 父结点比其子结点都小，最小的数在最上面，称为小顶堆

• 如果要实现从小到大的升序排序，可以采用大顶堆，相应的，降序排序的话就采用小顶堆

2. 堆排序

2.1 什么是堆排序

堆排序就是永远把最大或最小的数扔在顶上。
堆排序（Heapsort）是利用二叉堆的概念来排序的选择排序算法，分为两种：

• 升序排序：利用最大堆进行排序
• 降序排序：利用最小堆进行排序

2.2 算法原理

2.2.1 理解方法1

再对上面已经变为完全二叉树的数据，再将其变为大顶堆
按照大顶堆的概念，父结点比其子结点都大，由于叶子结点没有子树，无法对比，因此只对非叶子结点4、2、8、0调整，进行初始化堆
给了一个数组，可以将其理解为完全二叉树，但还不满足堆的条件，需要初始化堆调整为堆。

• （1）初始化堆
  第一步：总共9个数，9/2=4，可以发现数组元素的个数除以2，正好是最后一个非叶子结点，从len/2往前遍历完每一个非叶子结点
  找到0，与其左右子树比较调整，具体代码如下：

int index = len/2; //当前调整的结点
//拿到最后一个非叶子结点及左右子树下标

int lchild = index*2; //最后一个非叶子结点的左子树下标
int rchild = index*2+1;//最后一个非叶子结点的右子树下标
int max = index; //最后一个非叶子结点下标

//进行判断
if(arr[lchild] > arr[max])
{
max = lcild;
}
if(arr[rchild] > arr[max])
{
max = rcild;
}
if

完成0位置结点的大顶堆比较交换，遍历完成4、2、8的结点的遍历交换，直至9到堆顶，这也就完成了初始化堆，形成一个基础的堆，如下：

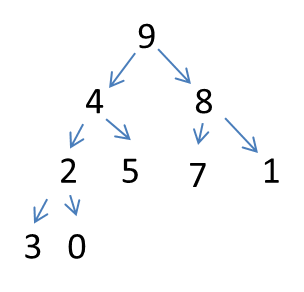
• （2）堆的排序调整
  第二步：堆已有的情况下，最大的值就在堆顶，对于数组下标即为0的位置，对于二叉树来说就是1号位置，将9与尾部的0交换（此处需要注意，视频中遗忘了左子树的比较，所以还是左子树数据存在问题，以右子树来理解思路）
  

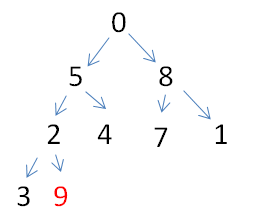
此时的堆顶的0结点不符合大顶堆概念，从该结点开始从上往下调整

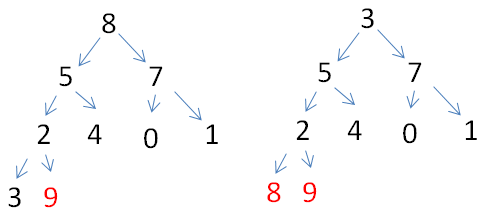
实现头和尾交换一次就调整一次，堆排序就是调整的过程

初始化的时候，从下往上调整，i=len / 2 --为开始调整非叶子结点就变为堆
从上往下调整，结束条件为>=len/2

2.2.2 理解方法2

给定一个最大堆如下图所示，以该最大堆进行演示堆排序

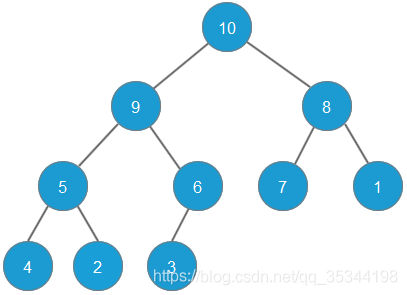
首先，删除堆顶元素10（即最大的元素），并将最后的元素3补充到堆顶，删除的元素10，放置于原来最后的元素3的位置

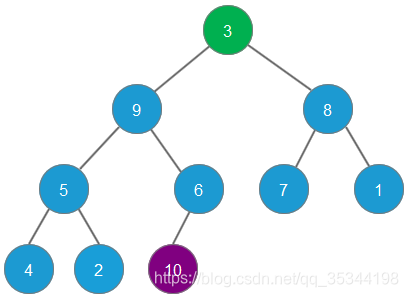
根据二叉堆的自我调整，第二大的元素9会成为二叉堆新的堆顶

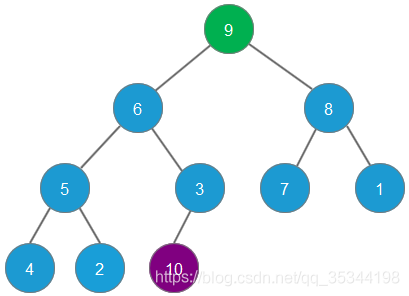
删除元素9，元素8成为最大堆堆顶

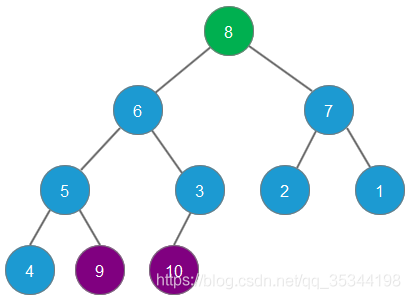
删除元素8，元素7成为最大堆堆顶

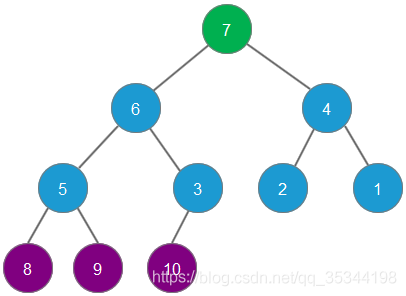
依次删除最大元素，直至所有元素全部删除

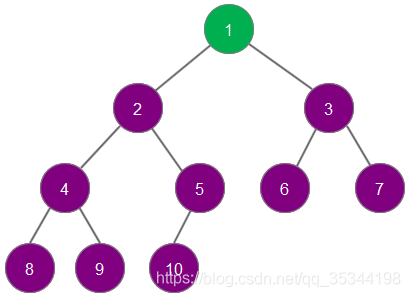
此时，被删除的元素组成了一个从小到大排序的序列

2.3 算法实现

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
using namespace std;

void PrintArray(int arr[],int len)
{
	for (int i = 0; i < len; i++)
	{
		cout << arr[i] << " ";
	}
	cout << endl;
}

void MySwap(int arr[],int a,int b)
{
	int temp = arr[a];
	arr[a] = arr[b];
	arr[b] = temp;
}

/*
@param myArr 待调整的数组
@param index 待调整的结点的下标
@param len 数组的长度
*/
void HeapAdjust(int arr[], int index, int len)
{
    //先保存当前结点的下标
	int max = index;
	//保存左右孩子的数组下标
	int lchild = index * 2 + 1;
	int rchild = index * 2 + 2;

	if (lchild < len && arr[lchild]>arr[max])
	{
		max = lchild;
	}
	if (rchild < len && arr[rchild]>arr[max])
	{
		max = rchild;
	}

	if (max != index)
	{
		//调整后还有不满足大顶堆的，交换两个节点
		MySwap(arr, max, index);
		HeapAdjust(arr, max, len);
	}
}

//堆排序
void HeapSort(int myArr[], int len)
{
	//初始化堆
	for (int i=len/2-1;i>=0;i--)
	{
		HeapAdjust(myArr, i, len);
	}

	//交换堆顶元素和最后一个元素
	for (int i=len-1;i>=0;i--)
	{
		MySwap(myArr, 0, i);
		//交换之后，需要重新进行调整堆
		HeapAdjust(myArr, 0, i);
	}
}

int main(void)
{
	int myArr [] = {4,2,8,0,5,7,1,3,9};
	int len = sizeof(myArr) / sizeof(int);
	PrintArray(myArr,len);

	//堆排序
	HeapSort(myArr, len);
	PrintArray(myArr, len);

	return 0;
}

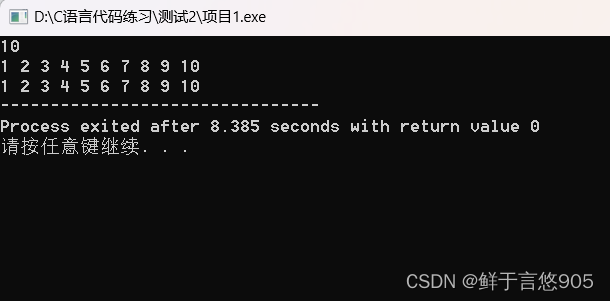
运行结果：

3. 堆排序算法特点

3.1 时间复杂度

下沉调整的时间复杂度等同于堆的高度O(logn)，构建二叉堆执行下沉调整次数是n/2，循环删除进行下沉调整次数是n-1，时间复杂度约为O(nlogn)

3.2 空间复杂度

堆排序算法排序过程中需要一个临时变量进行两两交换，所需要的额外空间为1，因此空间复杂度为O(1)

3.3 稳定性

堆排序算法在排序过程中，相同元素的前后顺序有可能发生改变，所以堆排序是一种不稳定排序算法

4. 视频地址：堆排序思路，堆排序代码