ArXiv：https://arxiv.org/abs/1810.04805

github：GitHub - google-research/bert: TensorFlow code and pre-trained models for BERT

 

一、模型及特点：

1、模型：

        深层双向transformer encoder结构

        BERT-BASE：(L=12, H=768, A=12）

        BERT-LARGE：(L=24, H=1024, A=16）

2、特点：

        不同任务使用统一架构，预训练和微调只有很小不同

        双向预训练模型——通过训练MLM子任务获得

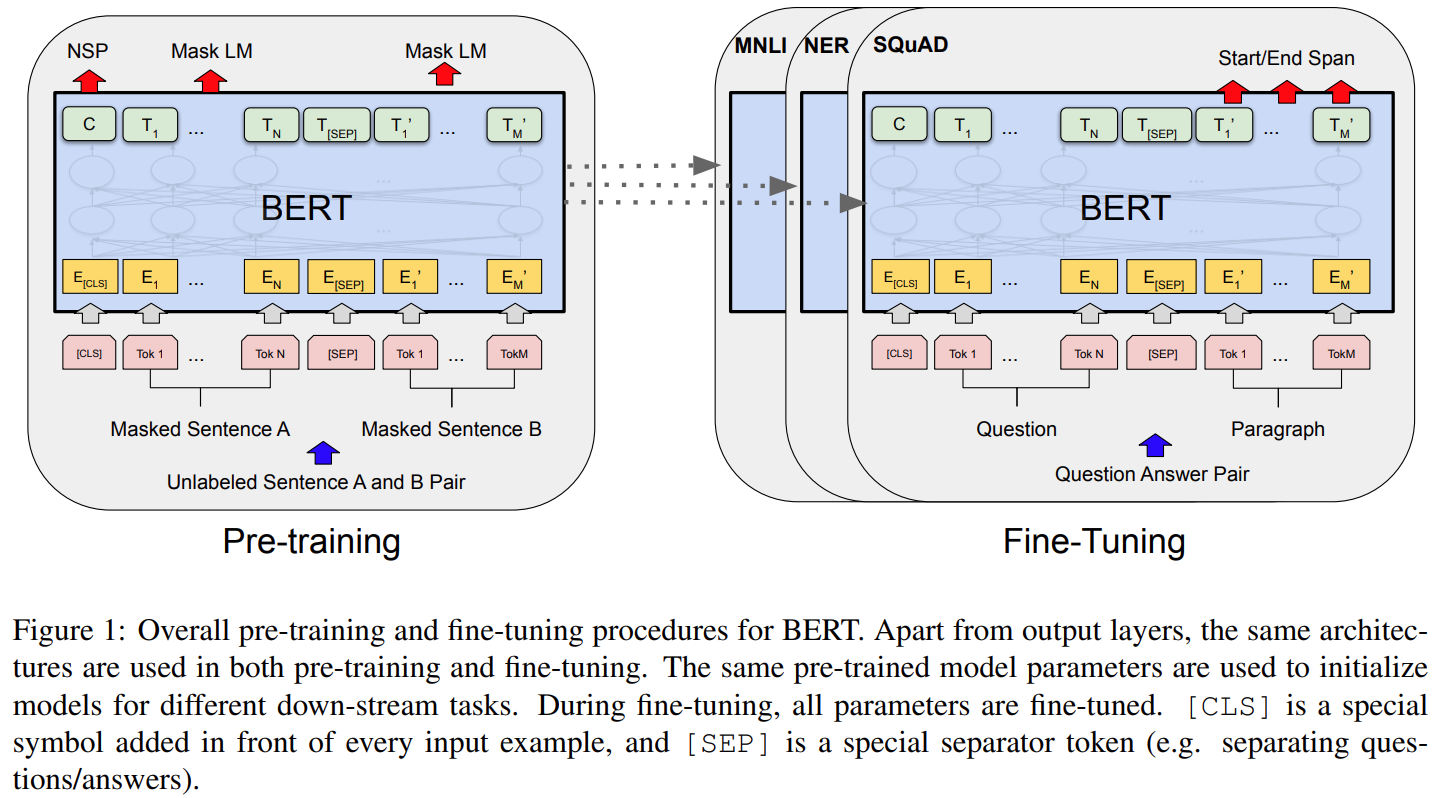
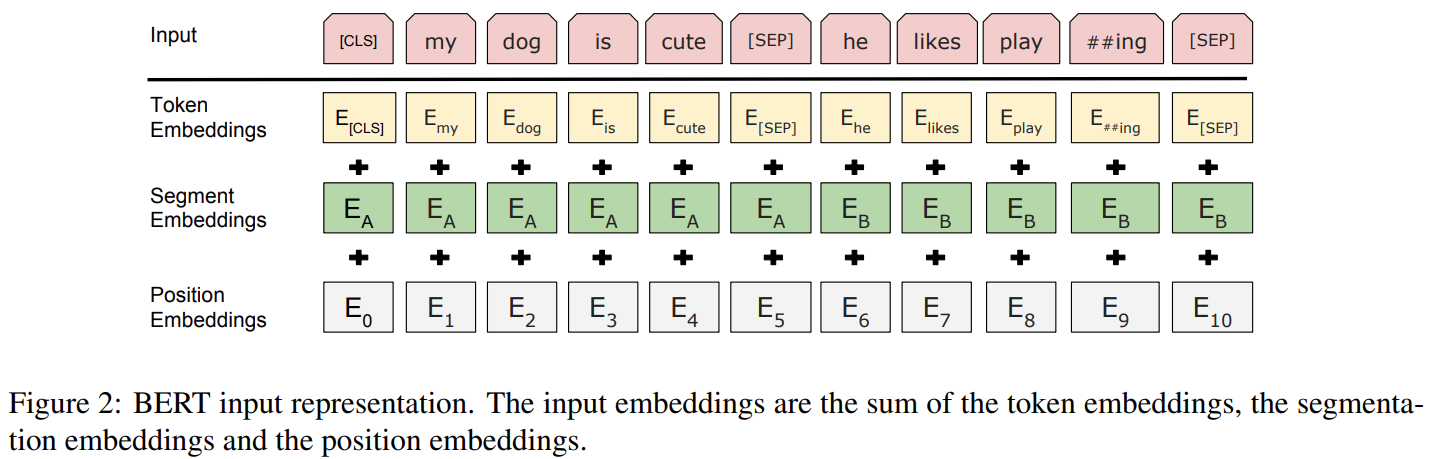
二、训练：两阶段训练——预训练和微调

1、预训练：

        （1）训练设置

            1）在无标签、不同任务上训练

            2）训练两个子任务：Masked LM（MLM）,Next Sentence Prediction (NSP)

                 MLM：为了双向模型

                        损失函数：cross entropy loss

                        mask：随机选择15%的位置，被选择的位置有80%mask，10%随机token，10%unchanged。训练中位置不变，但是由于每个句子不一样，所以预测的token也不是每次都一样。

                 NSP：为了理解句子关系

        （2）数据：

            BooksCorpus (800M words)、English Wikipedia (2,500M words)  extract only the text passages and ignore lists, tables, and headers.

2、微调：

预训练参数初始化，针对不对任务在有标签数据的所有参数微调，不同任务各自单独微调。

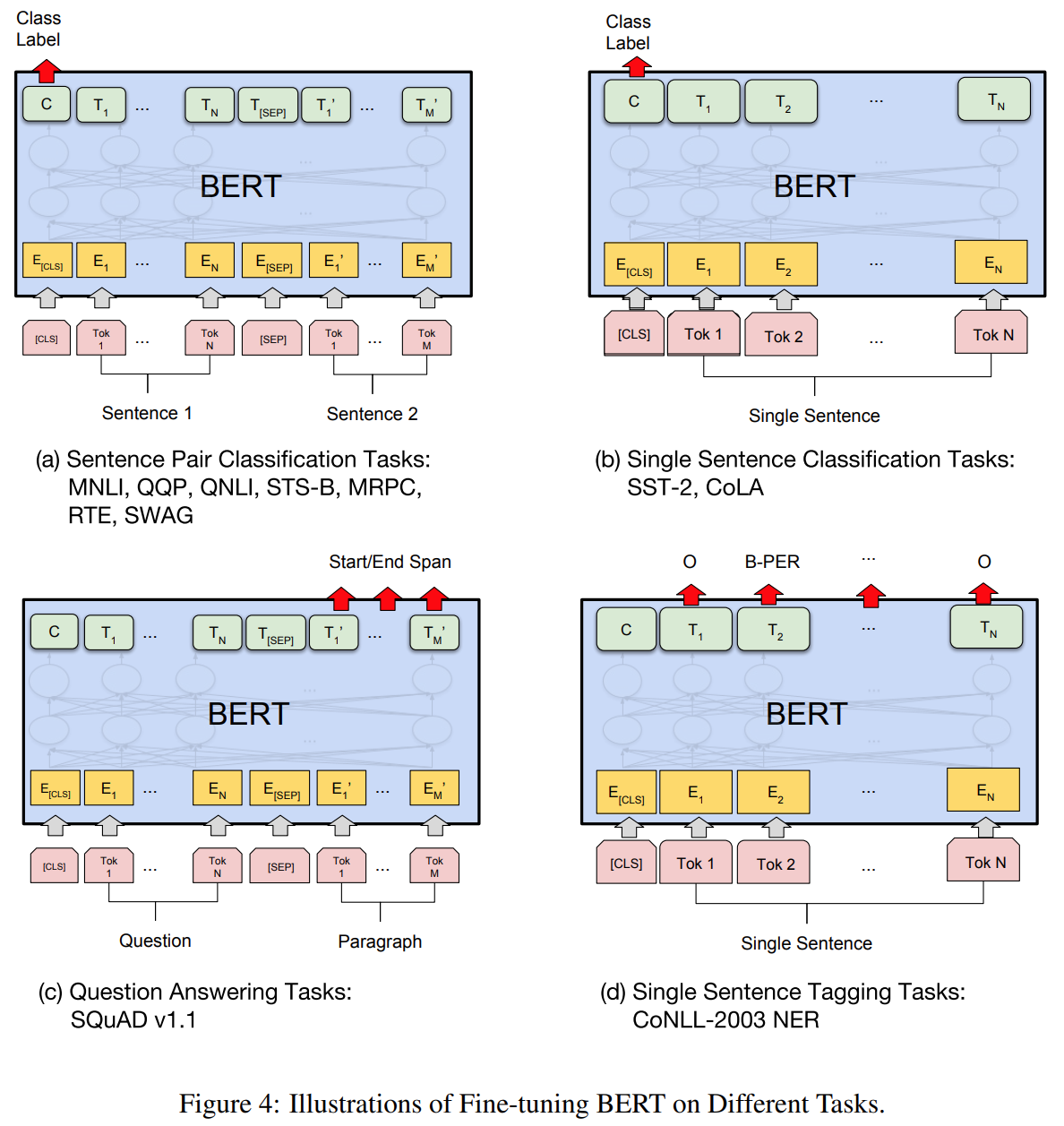
三、实验：

1、数据：

GLUE、SQuAD v1.1（问答。损失函数-最大似然，首先在TriviaQA上微调，然后在SQuAD 上微调）、SQuAD v2.0（没有在TriviaQA上微调）、The Situations With Adversarial Generations (SWAG)