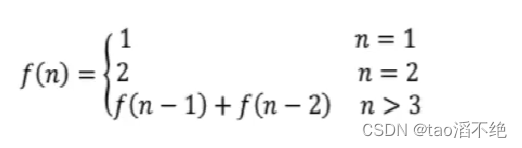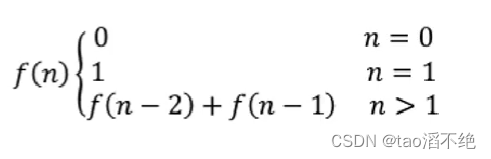目录
70:爬楼梯
题目要求:
解题思路:(类似斐波那契数)
递归解法:
非递归解法:
126:斐波那契数
题目要求:
解题思路:
递归解法:
非递归解法:
都看到这了,点个赞再走呗,谢谢谢谢谢!!!
70:爬楼梯
题目要求:
解题思路:(类似斐波那契数)
递归解法:
由题可知,每次可以爬1个或者2个台阶,假如有n个台阶,会有多少种走法?那么我们就想,第一次爬一个台阶,那方法数就是爬这一次台阶加上剩下n-1个台阶的走法,爬两个台阶,那方法数就是爬完这两个台阶再加上剩下n-2个台阶的走法,很容易就想到递归的解法了,而使用递归我们要找到终止条件,也要写出递归公式
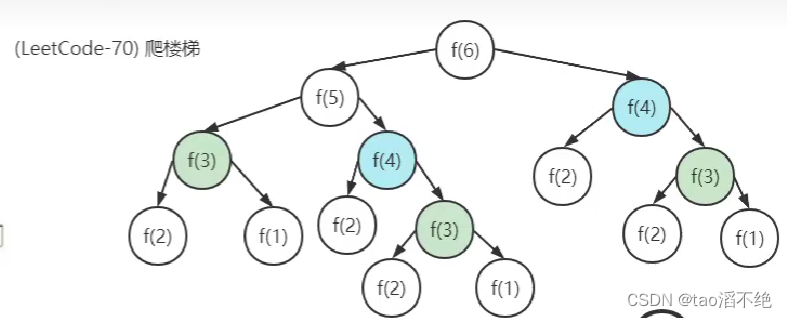
但是这么递归的时间复杂度很高,LeetCode上通过不了,会有很多重复计算的斐波那契数,我们可以用HashMap来解题,每次往下找之前都记录一下map里面有没有n这个斐波那契数,有就不用继续往下找了,直接返回这个斐波那契数,没有就继续往下找,有了HashMap的引用,我们时间复杂度就变成了O(N),在LeetCode上也就能通过了。
递归公式如下:
代码如下:
class Solution { HashMap<Integer, Integer> hashmap = new HashMap<>(); public int climbStairs(int n) { if(n == 1) { return 1; } if(n == 2) { return 2; } //每次递归都判断map有没有n个台阶爬楼梯方法数,没有算出当前n阶台阶的方法数,放进map里,放进map里后就不用继续往下递归了,直接返回这个方法数,因为hashmap已经存了n阶台阶的方法数了;有就不用继续递归了,直接返回n台阶的方法数 if(hashmap.get(n) != null) { return hashmap.get(n); } else { int result = climbStairs(n - 1) + climbStairs(n - 2); hashmap.put(n, result); return result; } } }非递归解法:
从此图我们可以看出,要求n的斐波那契数,必须求前一个和前两个的斐波那契数,也就是上图的公式,非递归的解法,我们就用循环来解决,从下至上来求n的斐波那契数,我们定义一个pre和prePre变量来记录前一个和前两个的斐波那契数,result来记录n的斐波那契数,每循环一次都要更改pre和prePre的下标,时间复杂度为O(N).
代码如下:
public int climbStairs(int n) { //非递归思想 if(n == 1) { return 1; } if(n == 2) { return 2; } int result = 0; int pre = 2; int prePre = 1; for(int flg = 3; flg <= n; flg++) { result = pre + prePre; //pre和prePre都要往前推 prePre = pre; pre = result; } return result; }
126:斐波那契数
题目要求:
解题思路:
这题和爬楼梯思路一样,解法也一样,递归和非递归也一样,不过他的递归公式和结束条件和爬楼梯不一样,公式如下图:
递归思路:因为递归会重复计算很多次,所以我们可以用一个HashMap来记录n的斐波那契数,每递归一次都判断map里面有没有n的斐波那契数,有就不用继续往下递归了,直接返回这个斐波那契数,没有就往下递归,把1后面的斐波那契数列都记录在map中,这样时间复杂度就是O(N)了,LeetCode也能通过。
非递归思路:用循环,从下至上,求得每个斐波那契数,我们定义result放n的斐波那契数,pre放n的前一个斐波那契数,prePre放n的前两个斐波那契数,每循环一次都要更新一次pre和prePre的下标,往上走。
递归解法:
代码如下:
Map<Integer, Integer> map = new HashMap<>(); public int fib(int n) { if(n == 0 || n == 1) { return n; } if(map.containsKey(n)) { return map.get(n); } //n的斐波那契数不在map里 int result = (fib(n - 1) + fib(n - 2)) % 1000000007; //int result = (fib(n - 1) + fib(n - 2)); map.put(n, result); return result; }
非递归解法:
public int fib(int n) { //非递归 if(n == 0 || n == 1) { return n; } int result = 0; int pre = 1; int prePre = 0; for(int i = 2; i <= n; i++) { result = (pre + prePre) % 1000000007; prePre = pre; pre = result; } return result; }