前言
本文将会向您介绍二分查找法(查找左右端点),关于朴素的二分查找法已经在之前讲过了朴素二分查找您可以点此超链接
查找右端点
如果您仅仅是想要参考如何查找左右端点,可以直接跳转到下文的模板处
ps:以下是本文涉及到的一些名词
tar(target目标值):示例中所要查找的值
mid:中间位置下标
vue(value):中间位置的值与mid对应
R:right
L:left
ps:文中的图例皆来自手写笔记
首先你应该先要记住:查找左右端的思想->二段性
待查找目标值tar:3
我们将区间分为两段,分别是小于等于3,和大于3
你肯定会有疑问:为什么要这么分
->原因是我们每次计算的vue中间位置处的值要么是在大于等于tar区间内的,也有可能是在小于tar区间内的,已经涵盖了查找右端点的所有可能性,助于理解罢了
参考代码片段
//查找右端点
while (left < right)
{
int mid = left + (right - left + 1) / 2;
if (nums[mid] <= target)
{
left = mid;
}
else right = mid - 1;
}
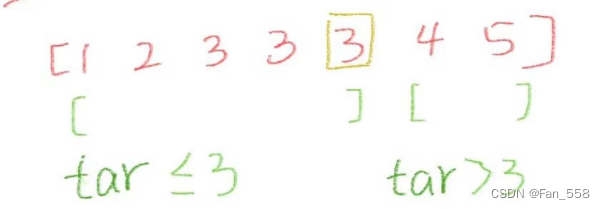
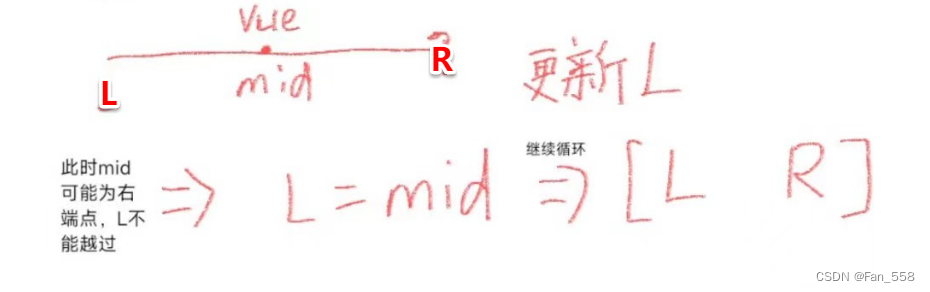
左区间:
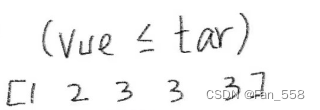
计算中间位置mid = L + (R - L + 1)/ 2(为什么会是这个计算式,见后文)
更新left(L):L = mid,本质上还是缩小区间
注意:L缩小区间不能是mid + 1,如果mid本身就是右端点,那么就永远查找不到了
更新完L,继续进循环重复步骤
右区间

由于要查找的target目标值不在此区间内,我们依旧还是模拟这个过程(虽然表面上已经不用再分析了),因此缩小区间范围
更新R(right) = mid - 1
尽量缩的小一点,因此给了mid - 1

继续进入循环,直至循环结束
循环条件讨论:left < right
为什么不像朴素的二分法一样left<=right呢
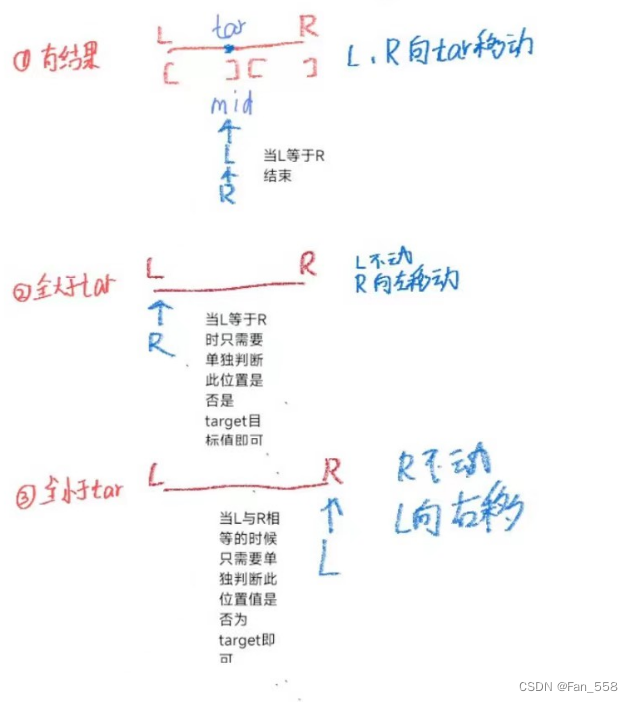
第一种情况:有结果
第二种情况:数组中的元素都比目标值大
第三种情况:数组中的元素都比目标值小
这三种情况我们都只需要单独判断最终位置的值和target的关系即可
如果这里用left<=right当循环条件判断,看第一种情况,当left == right的时候,会一直命中此条件,L=mid, 一直执行此条件,导致死循环
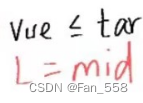
上文中留下了一个疑问:为什么我们查找右端点的中点公式是mid = L + (R - L + 1)/ 2
原因是:当剩余两个数的时候,如果target值是左边的数,那么我们采用mid = L + (R - L )/ 2
计算中点,中点计算出来的值将会是左侧的数,将会一直命中L = mid,导致死循环
查找左端点
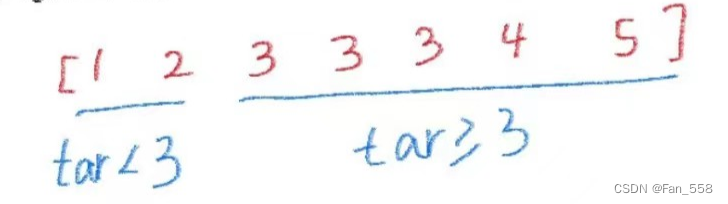
与查找右端点一样,我们将模拟所有的情况,因此我们把区间分为小于tar, 和大于等于tar
左区间

由于左区间不是target值所在的区间
我们更新L(left)的值,尽量向右移动(相比于给mid),因此给了mid + 1,然后继续循环直至循环结束
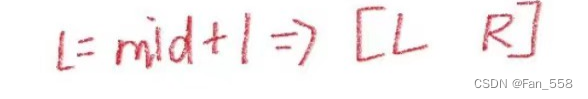
缩小右区间:
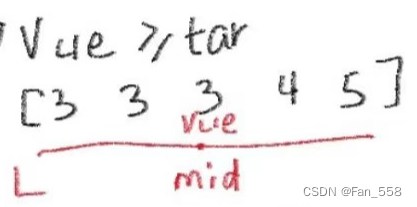
更新R(right),将R向左移,但是不能是mid-1,因为mid处的值可能就是目标值,要不然就永远找不到了

循环条件:left < right
为什么不是left <= right与查找右端点时的分析一样,结果会导致死循环,这里就不再多赘述
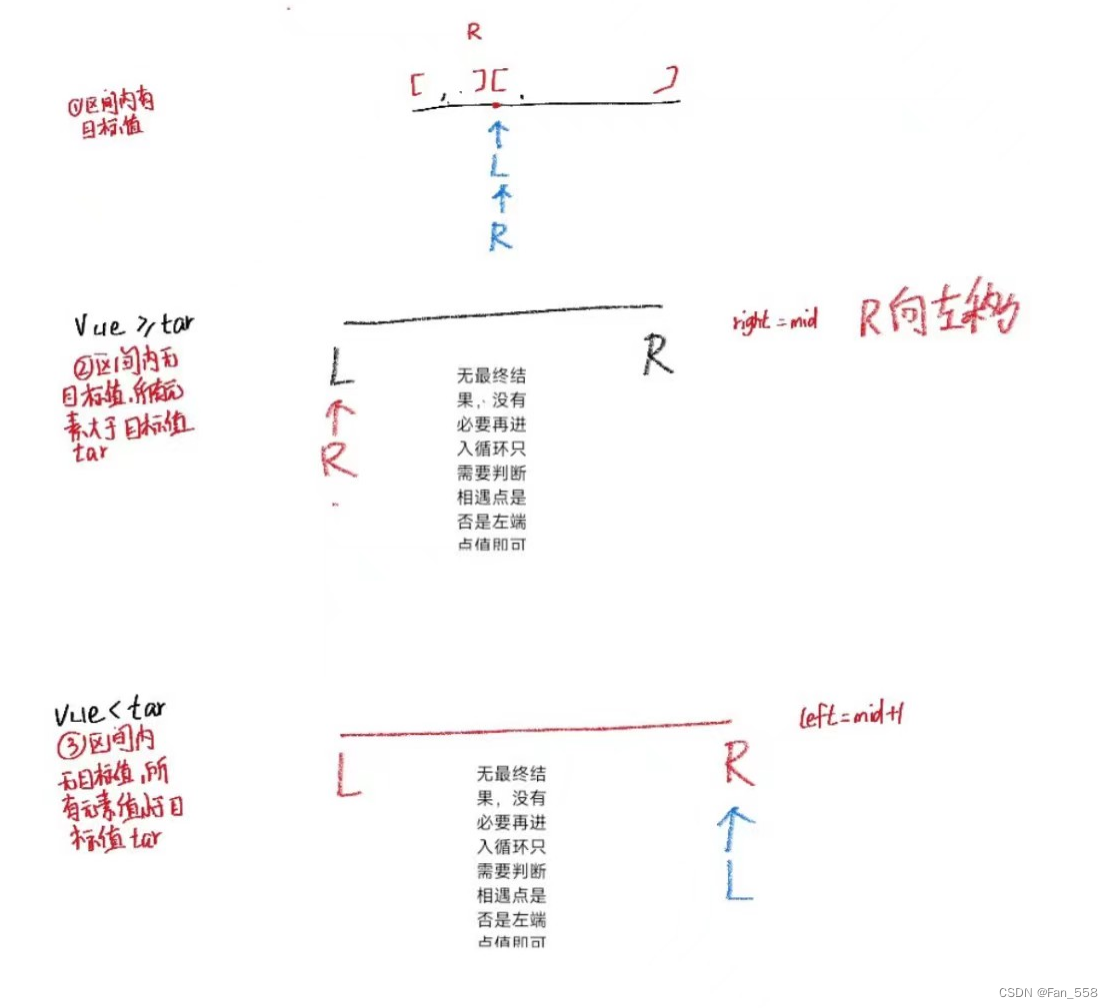
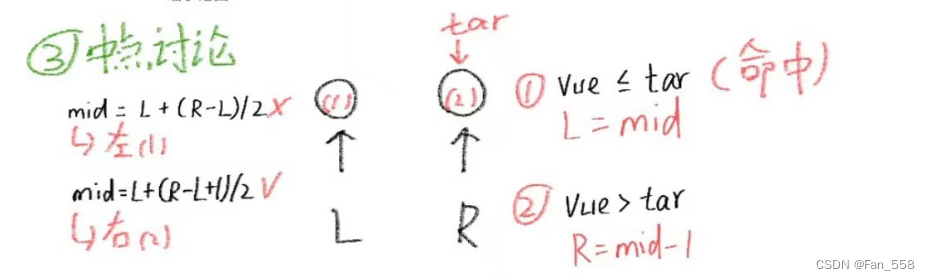
中点讨论:
注意:这里的中点计算公式是与查找右端点不同的!!!
当target在靠右的数的时候,第二个mid计算出的mid将会一直在tar位置,并会一直命中R=mid,会导致死循环
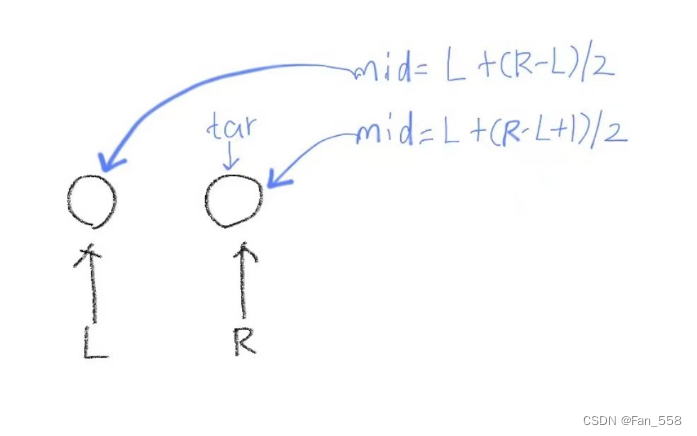
因此查找左端点的中点公式还是用mid = L + (R - L)/ 2
查找左右端点模板
while(left < right)
{
int mid = left + (right-left)/2
if(...) left = mid + 1;
else right = mid;
}
while(left < right)
{
int mid = left + (right - left + 1)/2
if(...) left = mid;
else right = mid - 1;
}
例题
如果你已经看完了上文,并能够自己分析出来,那么你可以尝试下面这道题
在排序数组中查找元素的第一个和最后一个位置
小结
今日的分享就到这里啦,如果本文存在疏漏或错误的地方还请您能够指出!