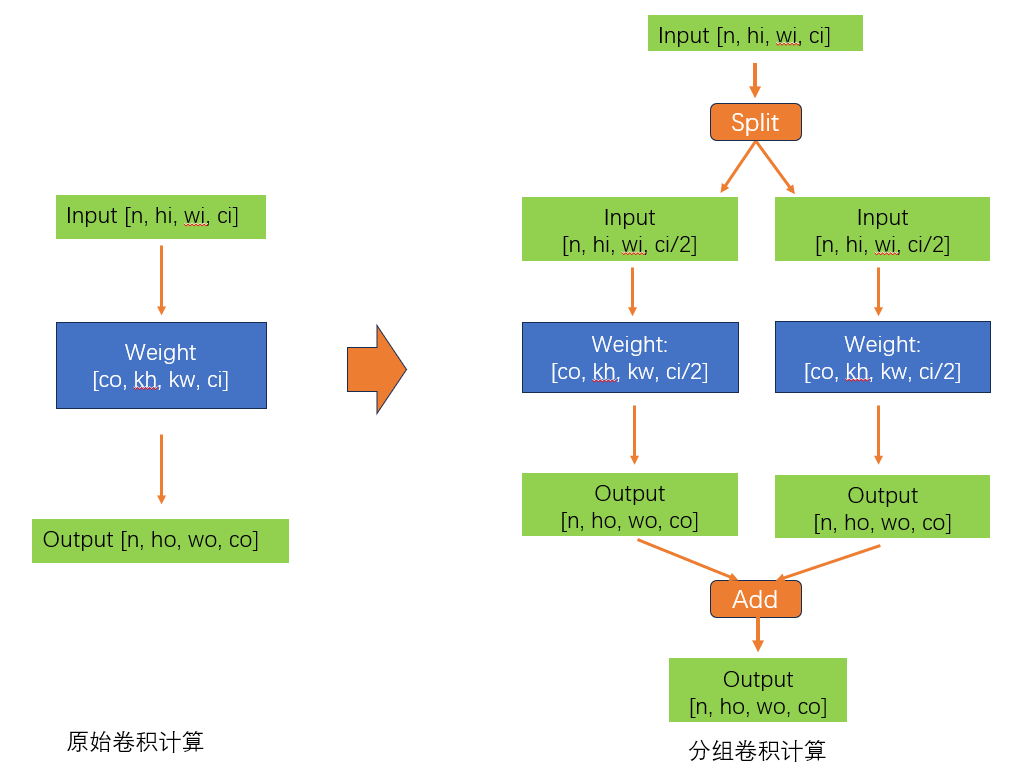
当然可以。首先,我们先了解一下2D地图的基本构成。2D地图实际上是一个网格系统,其中每个单元格(或像素)代表现实世界中的一个区域。当我们谈论origin时,我们实际上是在描述这个网格如何在真实的3D空间中放置。
让我们通过一个简单的示意图来解释:
假设上面的矩形表示一个2D地图,每个单元格代表现实世界中的一部分。
现在,当我们将这个地图放在机器人的坐标系统中时,我们需要知道其中一个点(通常是地图的中心或角落)在机器人坐标系统中的位置。这就是origin的作用。
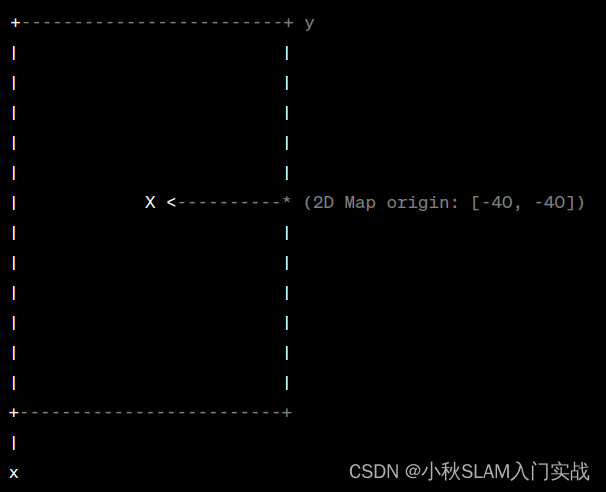
在上述示意图中,X是机器人的坐标原点(即 (0,0))。* 是2D地图的origin,在此例中为 (-40,-40)。这意味着地图的原点在机器人坐标系的x和y方向上都偏移了-40单位。
请注意,此图是为了说明而简化的。在实际应用中,origin可能还包括地图的旋转,但为了简洁性,我们在此省略了这一点。
希望这个示意图可以帮助您更好地理解origin的概念!
image