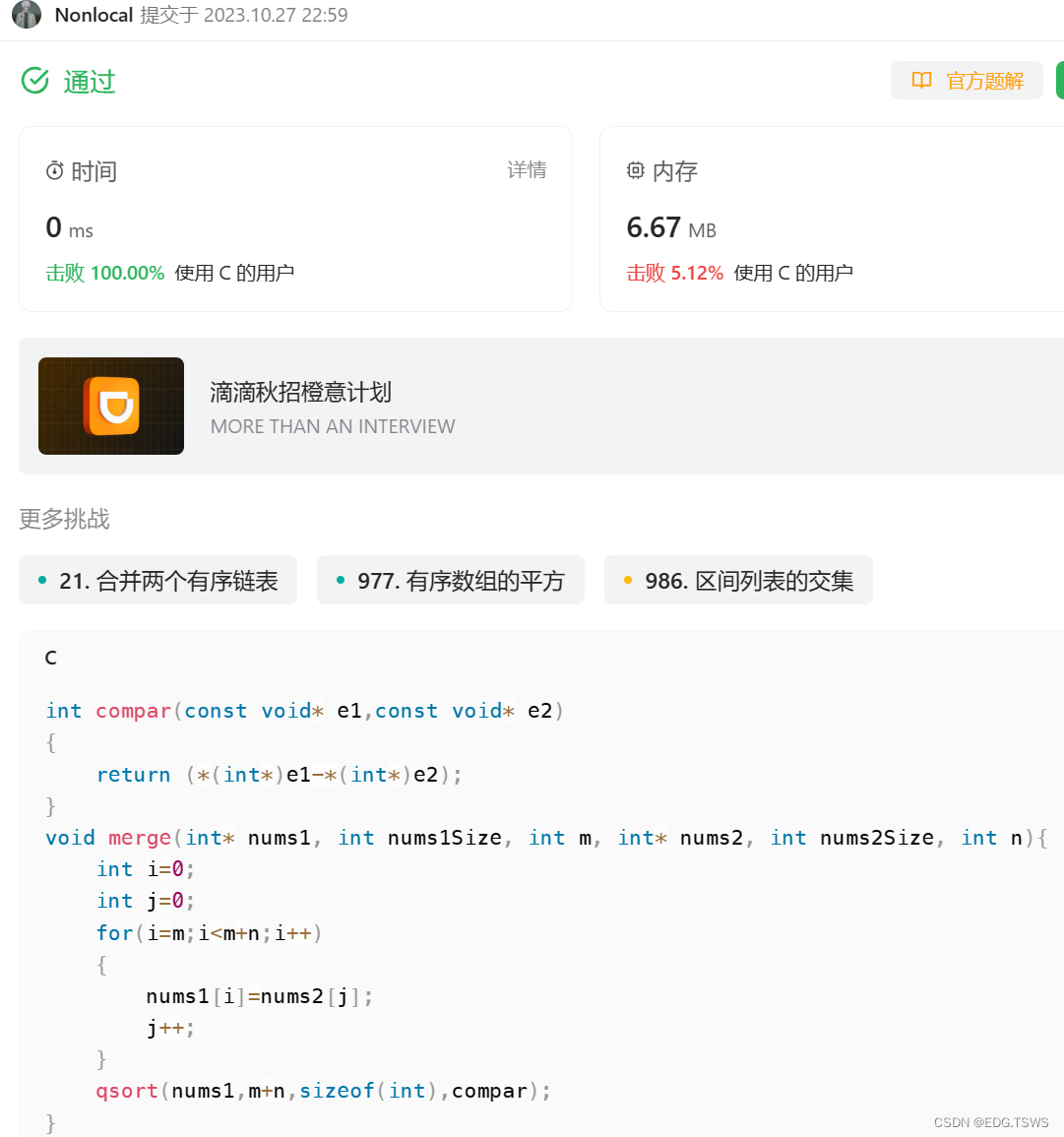
根据题意可以知道是一个动态规划,看完数据范围之后可以知道是一个线性DP。
解决方法有点类似于背包问题,枚举背包的每一个空间。
如果把坐标轴上每个点都看成一个块儿,只需要按顺序求出前 i 个块儿的最大牧草堆数,f[i] 就是前i的最大牧草堆数。
假如区间x, y 是一个牧草堆块儿,只需取 f[y - 1] 与 f[x - 1] + y - x + 1,前者就相当于这个堆块儿不取的情况下的最大数,后者相当于取当前堆块儿的最大数,取最大值即可。
因为枚举的是坐标轴上的所有位置,所以每一个位置的最大值都可以从上一个位置更新过来,如果当前位置为某个堆块儿的右端点,只需要判断当前堆块儿取不取即可。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define endl "\n"
//#define x first
//#define y second
//#define int long long
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<int, string> pis;
typedef struct{
int x, y;
}aa;
const int mod = 1e9 + 7;
const int N = 3e6+ 10;
int dx[] = {-1, 0, 1, 0, -1, 1, 1, -1};
int dy[] = {0, 1, 0, -1, 1, 1, -1, -1};
int n, m;
int x, y;
vector<int> vec[N];
int f[N];
inline void sovle()
{
cin >> n;
int r = 0;
for(int i = 0; i < n; i ++) // 用vector可以使代码更加简洁,不过空间有点悬。这一题还是行的
{
int a, b;
cin >> a >> b;
vec[b].push_back(a - 1); // 记录当前右端点对应的左端点,减一有利于之后的计算。
r = max(b, r); // 记录最大右端点
}
for(int i = 1; i <= r; i ++)
{
f[i] = f[i - 1];
for(auto j : vec[i]) //枚举以当前位置为右端点的所有堆块儿
{
f[i] = max(f[i], f[j] + i - j); // 通过状态转移方程来更新当前位置。
}
}
cout << f[r] << endl; // 输出最大值
}
signed main(void)
{
IOS;
int t = 1;
// cin >> t;
while(t --) sovle();
return 0;
}