A星寻路算法
- 第一步
- 第二步
- 第三步
- 第四步
- JAVA实现
用于寻找有效路径的算法。
定义俩个集合
OpenList:可到达的格子
CloseList:已到达的格子
每一个格子都具有F、G、H这3个属性
- G:从起点走到当前格子的成本,也就是已经花费了多少步。
- H:在不考虑障碍的情况下,从当前格子走到目标格子的距离,也就是离目标还有多远。
- F:G和H的综合评估,也就是从起点到达当前格子,再从当前格子到达目标格子的总步数。
- 公式如下:F = G + H
在下面例子中,格子的左下方数字是G,右下方是H,左上方是F。
第一步
把起点放入OpenList,也就是刚才所说的可到达格子的集合
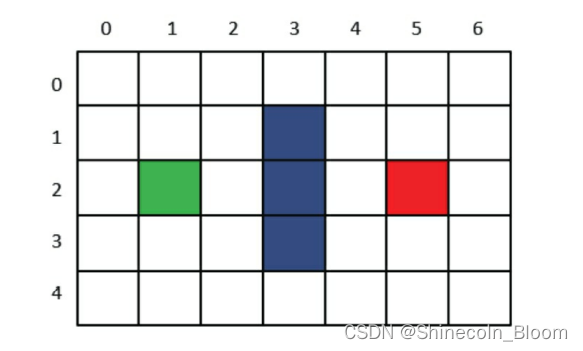
OpenList:Grid(1,2)
CloseList:
第二步
找出OpenList中F值最小的方格作为当前方格
(此时OpenList中只有唯一的方格Grid(1,2),把当前格子移出OpenList,放入CloseList)
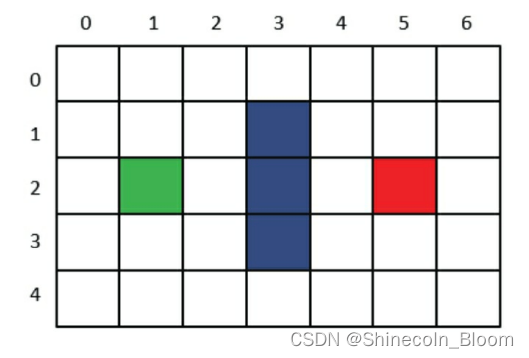
OpenList:
CloseList:Grid(1,2)
第三步
找出当前方格(刚刚检查过的格子)上、下、左、右所有可到达的格子,看它们是否在OpenList或CloseList当中。如果不在,则将它们加入OpenList,计算出相应的G、H、F值,并把当前格子作为它们的“父节点”。
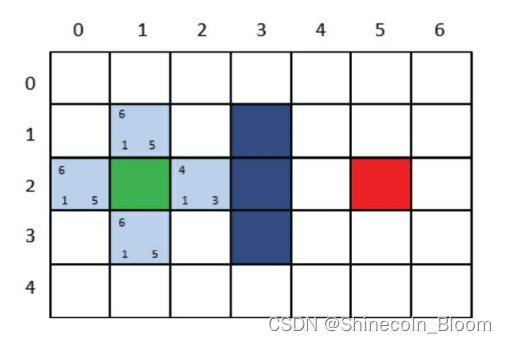
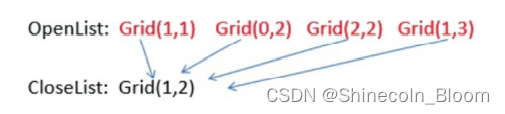
一个格子的“父节点”代表它的来路,在输出最终路线时会用到
第四步
重复刚才的第2步和第3步,直到找到终点为止
启发式搜索:以估值高低来决定搜索优先次序的方法
JAVA实现
package practice;
import java.util.ArrayList;
import java.util.List;
public class AStar {
//迷宫地图
public static final int[][] MAZE = {
{ 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 1, 0, 0, 0 },
{ 0, 0, 0, 1, 0, 0, 0 },
{ 0, 0, 0, 1, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0 }
};
/**
* A星寻路主逻辑
* @param start 迷宫起点
* @param end 迷宫终点
*/
public static Grid aStarSearch(Grid start, Grid end) {
ArrayList<Grid> openList = new ArrayList<Grid>();
ArrayList<Grid> closeList = new ArrayList<Grid>();
//把起点加入 openList
openList.add(start);
//主循环,每一轮检查一个当前方格节点
while (openList.size() > 0) {
// 在openList中查找 F值最小的节点作为当前方格节点
Grid currentGrid = findMinGird(openList);
// 当前方格节点从openList中移除
openList.remove(currentGrid);
// 当前方格节点进入 closeList (表示 已达 )
closeList.add(currentGrid);
// 找到currentGrid节点的所有邻近节点
List<Grid> neighbors = findNeighbors(currentGrid, openList, closeList);
for (Grid grid : neighbors) {
//邻近节点不在openList中,标记父亲、G、H、F,并放入openList
grid.initGrid(currentGrid, end);
openList.add(grid);//这一些节点 可达
}
//如果终点在openList中(可达终点),直接返回终点格子
for (Grid grid : openList){
if ((grid.x == end.x) && (grid.y == end.y)) {
return grid;
}
}
}
//openList用尽,仍然找不到终点,说明终点不可到达,返回空
return null;
}
//在openList中遍历所有元素,查找 F值最小的节点
private static Grid findMinGird(ArrayList<Grid> openList) {
Grid tempGrid = openList.get(0);
for (Grid grid : openList) {
if (grid.f < tempGrid.f) {
tempGrid = grid;
}
}
return tempGrid;
}
/**
* 找到grid节点的所有邻近节点,存储到ArrayList类型的数组gridList中。
* @param grid 就是当前节点,找他的左右上下节点
* @param openList 可到达的格子
* @param closeList 已到达的格子
* @return 到达终点最优路径的那个节点(F值的最优)
*/
private static ArrayList<Grid> findNeighbors(Grid grid, List<Grid> openList, List<Grid> closeList) {
//用于存放grid的上下左右邻居节点
ArrayList<Grid> gridList = new ArrayList<Grid>();
//grid的左面节点
if (isValidGrid(grid.x, grid.y-1, openList, closeList)) {
gridList.add(new Grid(grid.x, grid.y - 1));
}
//grid的右面节点
if (isValidGrid(grid.x, grid.y+1, openList, closeList)) {
gridList.add(new Grid(grid.x, grid.y + 1));
}
//grid的上面节点
if (isValidGrid(grid.x-1, grid.y, openList, closeList)) {
gridList.add(new Grid(grid.x - 1, grid.y));
}
//grid的下面节点
if (isValidGrid(grid.x+1, grid.y, openList, closeList)) {
gridList.add(new Grid(grid.x + 1, grid.y));
}
return gridList;
}
//依据下标x,y来判断节点(x,y)是否实际可达
private static boolean isValidGrid(int x, int y, List<Grid> openList, List<Grid> closeList) {
//是否超过边界
if (x < 0 || x >= MAZE.length || y < 0 || y >= MAZE[0].length) {
return false;
}
//是否有障碍物
if(MAZE[x][y] == 1){
return false;
}
//是否已经在openList中
if(containGrid(openList, x, y)){
return false;
}
//是否已经在closeList中
if(containGrid(closeList, x, y)){
return false;
}
return true;
}
//判断List数组中是否有x,y值的节点
private static boolean containGrid(List<Grid> grids, int x, int y) {
for (Grid grid : grids) {
if ((grid.x == x) && (grid.y == y)) {
return true;
}
}
return false;
}
static class Grid {
public int x;
public int y;
public int f;
public int g; //从起点走到当前格子的成本,也就是已经花费了多少步。
public int h;
public Grid parent;
public Grid(int x, int y) {
this.x = x;
this.y = y;
}
/**
* 将可达的新节点初始化参数值(放入openList数组里面)
* @param parent 标记当前节点的父节点
* @param end 标记终点
* 根据parent节点的g,h,f值更新当前节点的值
* g 从起点走到当前格子的成本,也就是已经花费了多少步。g+1
* h 在不考虑障碍的情况下,从当前格子走到目标格子的距离,也就是离目标还有多远。
* f f = g + h
*/
public void initGrid(Grid parent, Grid end){
this.parent = parent;
this.g = parent.g + 1;
this.h = Math.abs(this.x - end.x) + Math.abs(this.y - end.y);
this.f = this.g + this.h;
}
}
public static void main(String[] args) {
//设置起点和终点
Grid startGrid = new Grid(2, 1);
Grid endGrid = new Grid(2, 5);
//搜索迷宫终点resultGrid (如果找不到就是null)
Grid resultGrid = aStarSearch(startGrid, endGrid);
//回溯迷宫路径
ArrayList<Grid> path = new ArrayList<Grid>();
while (resultGrid != null) {
path.add(new Grid(resultGrid.x, resultGrid.y));
resultGrid = resultGrid.parent;
}
//输出迷宫和路径,路径用星号表示
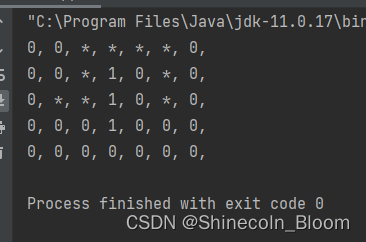
for (int i = 0; i < MAZE.length; i++) {
for (int j = 0; j < MAZE[0].length; j++) {
if (containGrid(path, i, j)) {
System.out.print("*, ");
} else {
System.out.print(MAZE[i][j] + ", ");
}
}
System.out.println();
}
}
}