目录
1.题目解析
2.讲解算法原理
2.1.如何来解决Pow问题?
2.2.为什么这道题可以用递归来做?
2.2.1 什么是递归
2.2.2 为什么会用到递归
3.如何编写递归代码?
4.递归的细节展开图
1.题目解析
50.Pow(x , n)
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,x^n )。
示例 1:
输入:x = 2.00000, n = 10 输出:1024.00000
示例 2:
输入:x = 2.10000, n = 3 输出:9.26100
示例 3:
输入:x = 2.00000, n = -2 输出:0.25000 解释:2-2 = 1/22 = 1/4 = 0.25
2.讲解算法原理
2.1.如何来解决Pow问题?

想要用递归解决这道题,我还是先讲一下我理解的递归,我们可以把递归所在的函数理解为一个黑盒子,在这个黑盒子中,他的功能能够完美实现你的需求,所以我们就需要相信它一定能够完成我想要的,这里同样
我们可以对当前数取根号,
当 n = 偶数 时当前数 = 当前数^(n/2) * 当前数^(n/2)
当 n = 奇数 时当前数 = 当前数^(n/2) * 当前数^(n/2) * 当前数^1
所以我们只需要让当前数不断的去衍生......
直到为1为止
2.2.为什么这道题可以用递归来做?
2.2.1 什么是递归
函数自己调用自己的情况
2.2.2 为什么会用到递归
在解决主问题的时候碰到相同的子问题
在解决子问题的时候又碰到相同的主问题

我们可以看到当前这道题的主问题都有相同的子问题,就是当前值等于子值的平方

3.如何编写递归代码?

class Solution {
public double myPow(double x, int n) {
return n < 0 ? 1.0 / pow(x,-n) : pow(x,n);
}
public double pow(double x,int n){
if (n == 0)return 1.0;
double tmp = pow(x,n / 2);
return (n % 2) == 0 ? tmp * tmp : tmp * tmp * x;
}
}
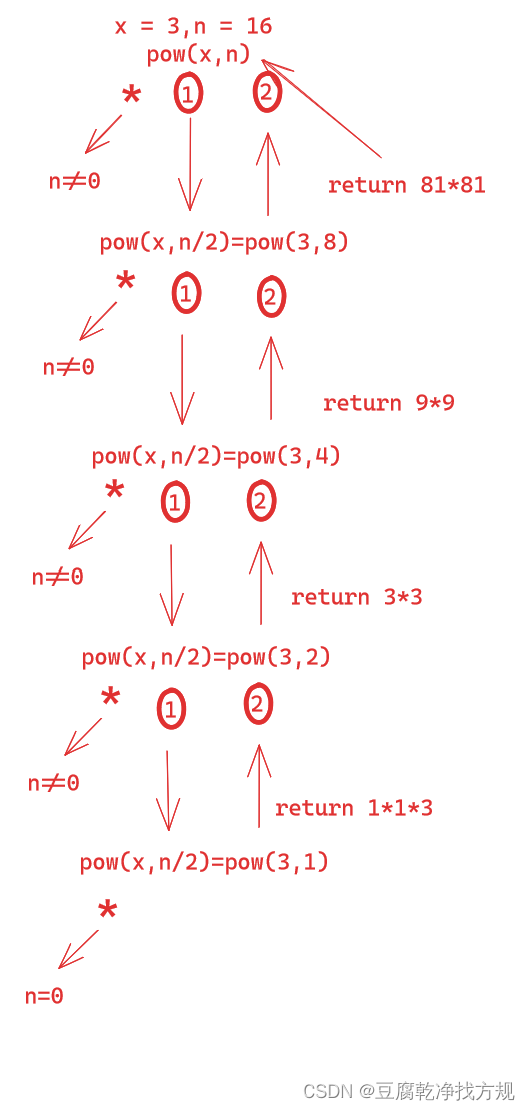
4.递归的细节展开图