二叉树的遍历
二叉树的基本结构:根节点(Data)、左子树(LChild)和右子树(RChild)。
因此只要依次遍历这三部分,就遍历了整个二叉树。
如果用L、D、R分别表示遍历左子树、访问根结点、遍历右子树,那么对二叉树的遍历顺序就可以有以下6种方式:
- 访问根,遍历左子树,遍历右子树,记作DLR。
- 访问根,遍历右子树,遍历左子树,记作DRL。
- 遍历左子树,遍历右子树,访问根,记作LRD。
- 遍历左子树,访问根,遍历右子树,记作LDR。
- 遍历右子树,遍历左子树,访问根,记作RLD。
- 遍历右子树,访问根,遍历左子树,记作RDL。
在以上6种遍历的方式中,如果规定按先左后右的顺序,那么就只剩下DLR、LDR和LRD三种。根据对根的访问先后顺序不同,分别称为DLR为先序遍历或先根遍历,LDR为中序遍历(对称遍历),LRD称为后序遍历。
注意,先序、中序、后序遍历都是递归定义的。
先序遍历(DLR)操作过程
若二叉树为空,则为空操作,否则依次执行如下三个操作:
- 访问根结点;
- 按先序遍历左子树;
- 按先序遍历右子树。
先序遍历实例

先序遍历实例解析:
- 先序遍历的本质是:以根结点为准,先遍历根结点;
- 然后在根结点的基础上,再依次遍历根结点左子树和右子树;
- 注意这里必须是要将根结点上的所有左子树都遍历完之后,再遍历根结点的右子树;
- 其中若是根结点的左子树还有很多结点,那么仍然是先遍历左子树,再遍历右子树。
答案:-+a*b-cd/ef
中序遍历(LDR)操作过程
若二叉树为空,则为空操作,否则依次执行如下三个操作:
- 按中序遍历左子树;
- 访问根结点;
- 按中序遍历右子树。
后序遍历(LRD)操作过程
若二叉树为空,则为空操作,否则依次执行如下三个操作:
- 按后序遍历左子树;
- 按后序遍历右子树;
- 访问根结点。
二叉树的遍历是一个递归过程。
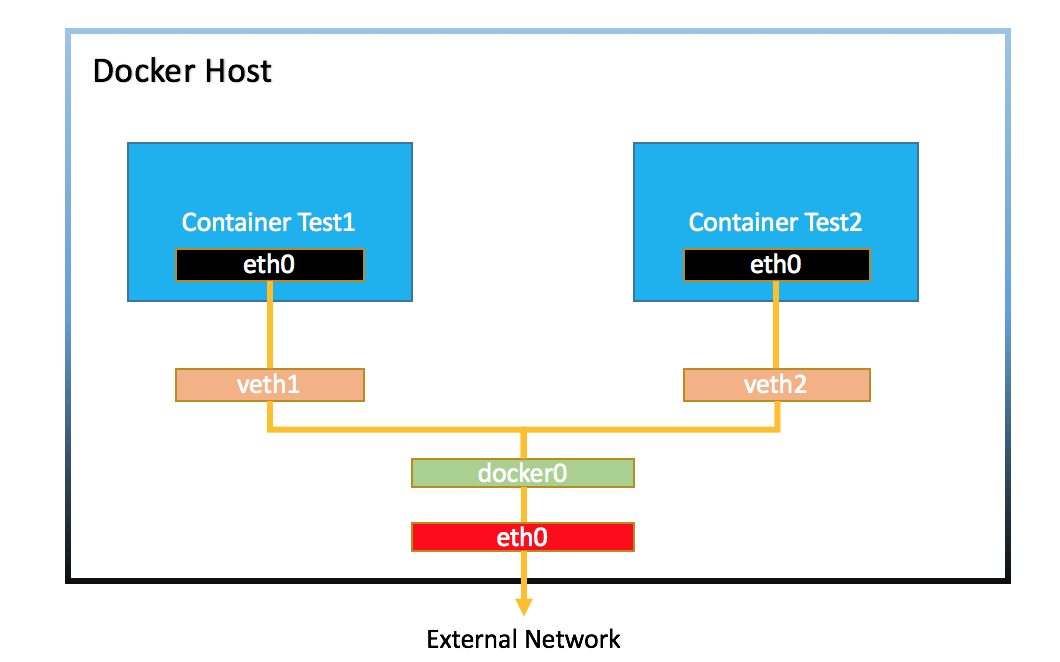
遍历实例一
先序遍历:ABDFGCEH
中序遍历:BFDGACEH
后序遍历:FGDBHECA
遍历实例二

先序遍历:-+a*bc/de
中序遍历:a+b*c-d/e
后序遍历:abc*+de/-
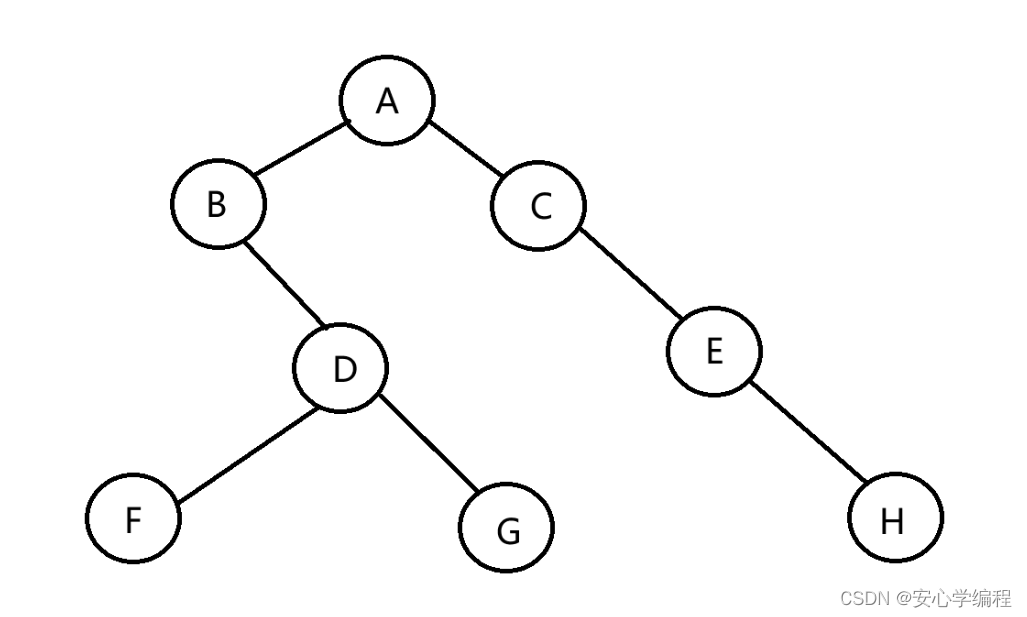
遍历实例三
先序遍历:ABDGCEFH
中序遍历:DGBAECHF
后序遍历:GDBEHFCA
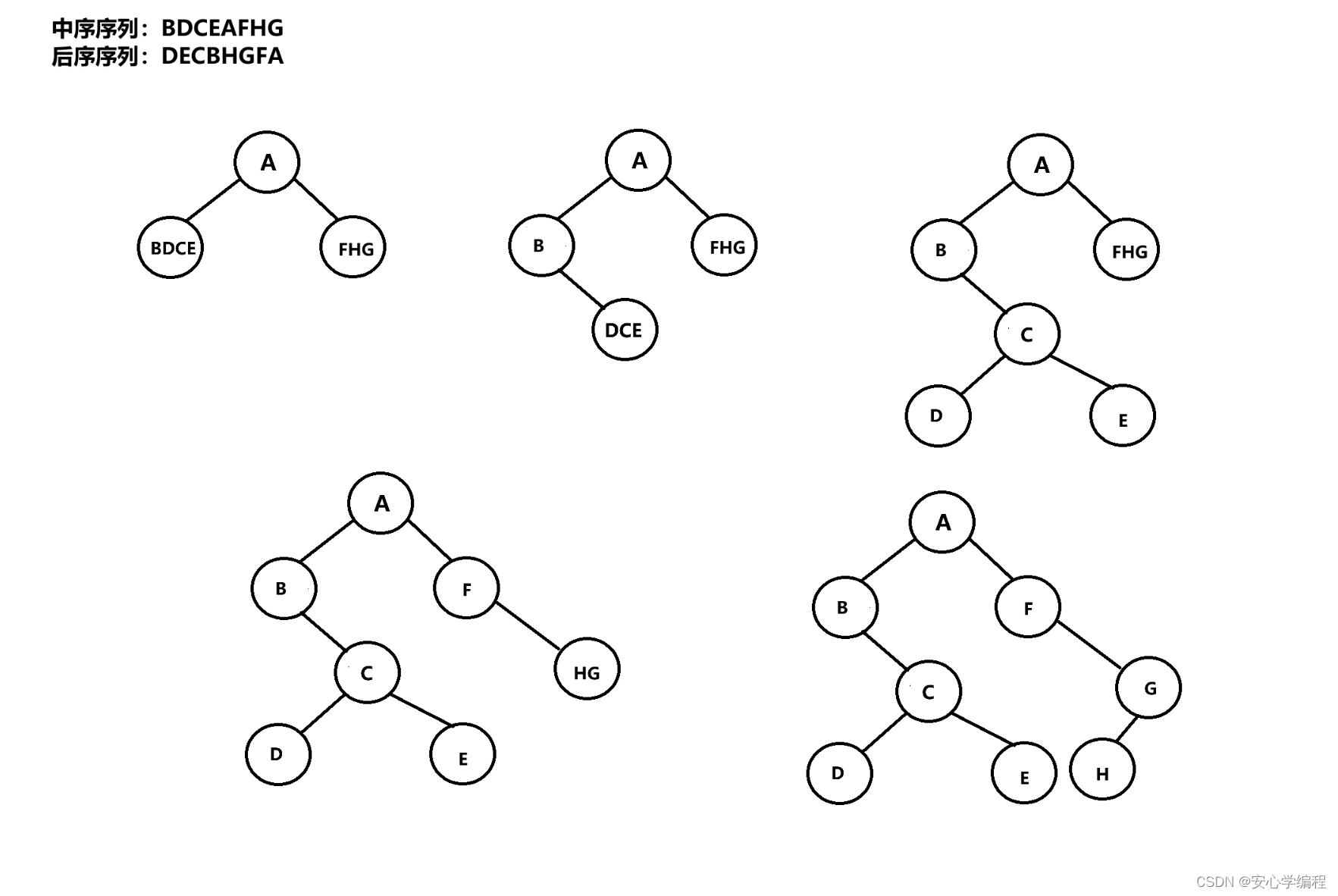
先中后序遍历必会练习题
练习:已知一棵二叉树的中序序列和后序序列分别为BDCEAFHG和DECBHGFA,画出这棵二叉树。
数的层次遍历利用队列来实现
算法思路
遍历从二叉树的根结点开始,首先将根结点入队列,然后指向下面的操作:
- 取出对头元素;
- 访问该元素所指结点;
- 若该元素所指结点的左、右孩子结点非空,则将该元素所指向结点的左孩子指针和右孩子指针入队。
- 若队列非空,重复前三步;当队列为空时,二叉树层次遍历结束。
层次遍历
二叉树的层次遍历:是指从二叉树的第一层(根结点开始),从上到下逐层遍历,在同一层中,按从左到右的顺序对结点逐个进行访问。
层次遍历实例

遍历结果:-+/a*efb-cd
二叉树的层次遍历算法
void LevelOrder(BiTree bt) //层次遍历二叉树bt算法
{
初始化队列;
if(bt==NULL) return;
bt入队列Q;
while(队列Q不空)
{
p←出队元素;
Visit(p); //访问出队结点
if(p->lchild) //队首结点左孩子不空,入队
{
p->lchild入队Q
}
if(p->rchild) //队首结点左孩子不空,入队
{
p->rchild入队Q
}
}
}创建二叉树总结
结合先序遍历序列和中序遍历序列创建二叉树
基本思路:先序遍历的第一个结点一定是二叉树的根结点,而根据中序遍历规则,这个结点将同一棵二叉树的中序遍历序列分成了左、右两部分,左边部分是二叉树的根结点的左子树的中序遍历序列,右边部分是二叉树的根结点的右子树的中序遍历序列。根据这两个子序列,在先序序列中找到对应的子序列,左子序列的第一个结点为左子树的根结点,右子序列的第一个结点为右子树的根结点。对左右子树,在反复利用这个方法,最终根据先序序列和中序序列能唯一地确定出一棵二叉树。
结合“扩展先序遍历序列”创建二叉树
扩展先序遍历序列:就是先对原有二叉树用空子树进行扩展,使每个结点的左右子树(包括空子树)都存在,然后再对扩展后的二叉树进行先序遍历。遍历序列中用特定的符号表示空子树。
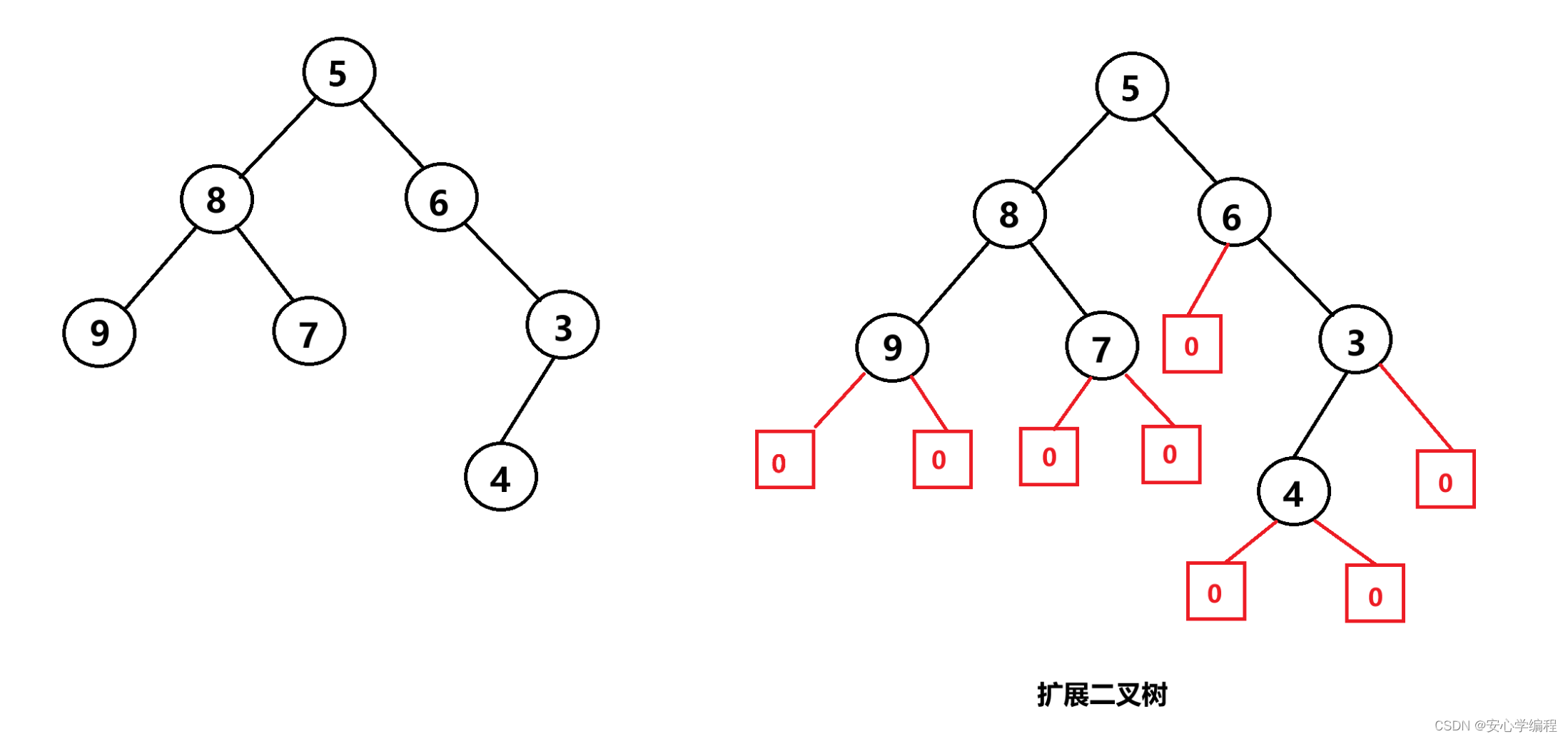
其扩展先序遍历序列为:
589007006034000
其中,“0”表示空子树。





![[ACTF2020 新生赛]Exec](https://img-blog.csdnimg.cn/a09460c15b174237a791667e68e5a344.png)