1、题目

问题描述

小蓝家要装修了，小蓝爸爸买了很多块（可理解为数量无限）$2\times 3$ 规格的地砖，小蓝家的地板是 $n\times m$ 规格的，小蓝想问你，能否用这些 $2\times 3$ 的地砖铺满地板。

铺满地板：对于地板的每个区域，都有且只有一块地砖覆盖，地砖可以旋转，但不能切割。

例如，对于 $7\times 6$ 的地板，一种铺地板方式是：

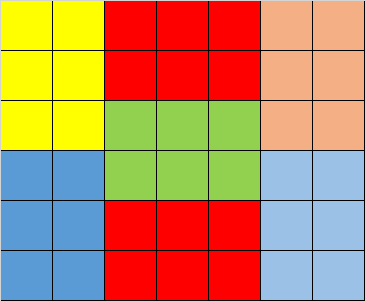
当然，也存在其他别的铺法。

小蓝家是个多层小别墅，每一层的规格不一样，所以他会多次询问你不同规格的地板。

注意：不要弄混地板和地砖。

输入格式

第一行输入一个整数 $T$，代表询问数量。
接下来 $T$ 行，每行两个正整数 $n_i,m_i$，代表小蓝询问的地板规格。

输出格式

对于每次询问，如果 $2\times 3$ 的地砖可以铺满地板，输出 Yes，否则输出 No。

样例输入

4
7 6
2 2
12 8
1 12

样例输出

Yes
No
Yes
No

数据范围

$1\le T\le 10^4，1\le n,m\le 10^4$

原题链接

铺地板

2、思路

分为如下情况：

1. $n\times m$ 不是 6 的倍数，不能铺满。
2. 如果是 6 的倍数，并且 $n$ 是 2 的倍数，$m$ 是 3 的倍数，可以铺满，或者反过来也行。（全部横放或者纵放）。
3. 如果 $n$ 既不是 2 也不是 3 的倍数，那么说明 $m$ 一定是 6 的倍数，那么只要 $n>1$，即可铺满，$n,m$ 调换也是合法的。

总结起来，如果 $n\times m$ 是 6 的倍数，那么只要 $n>1$ 且 $m>1$ 就是合法的。

简单证明3，有定理：两个互质的数，相互结合，不能组成的最大整数是 $a\times b-a-b$。那么 $2\times 3-2-3=1$，所以只有 1 不能拼成，考虑横着放一些，和纵放一些就行。

裴蜀定理：

若 $a,b$ 是整数,且 $gcd(a,b)=d$，那么对于任意的整数$x$，$y$，$ax+by$ 都一定是 $d$ 的倍数，特别地，一定存在整数$x$,$y$，使 $ax+by=d$ 成立。

3、代码

#include <iostream>
using namespace std;

int n, m;

void solve() {
    if ((n * m) % 6 == 0 && (n > 1) && (m > 1)) {
        cout << "Yes\n";
        return ;
    }
    cout << "No\n";
}

int main()
{
  ios_base::sync_with_stdio(false);
  cin.tie(NULL);

  int T;
  cin >> T;

  while (T--) {
      cin >> n >> m;
      solve();
  }
  return 0;
}