题目

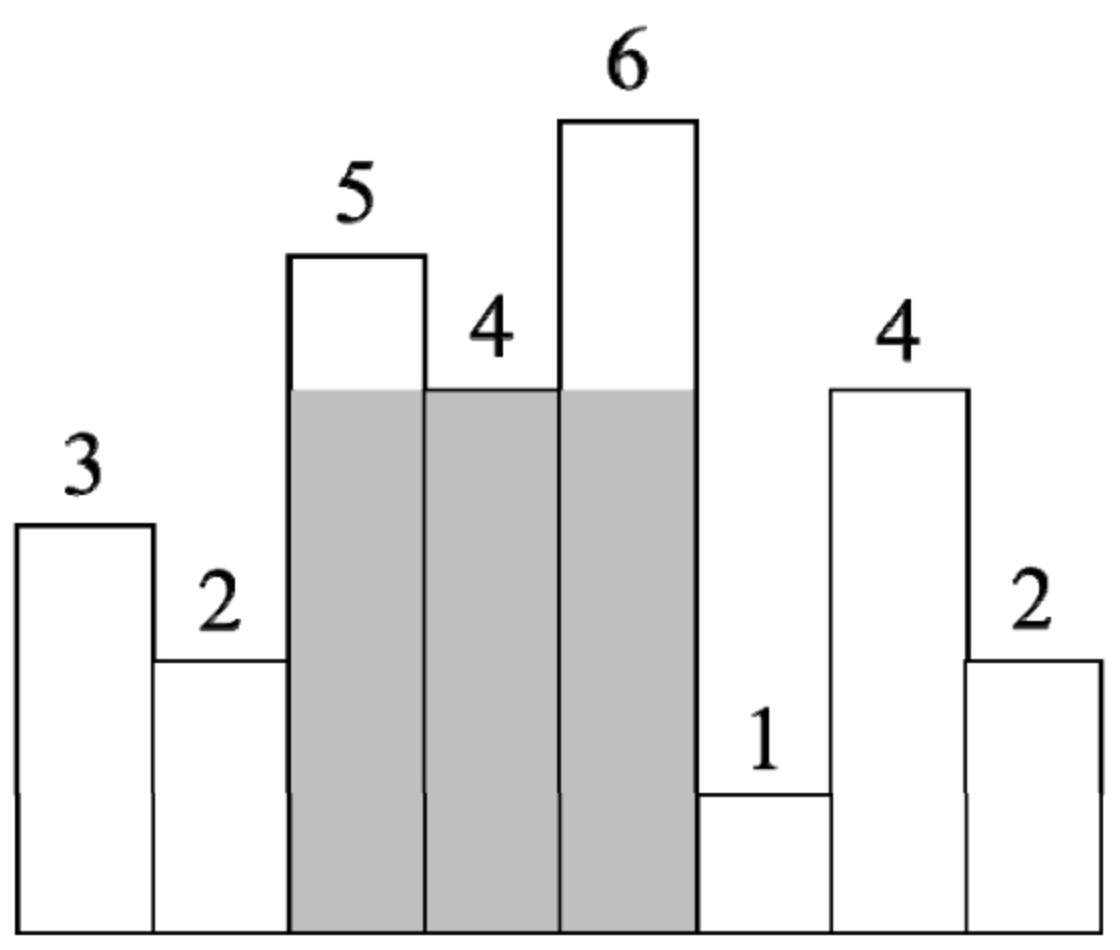
直方图是由排列在同一基线上的相邻柱子组成的图形。输入一个由非负数组成的数组，数组中的数字是直方图中柱子的高。求直方图中最大矩形面积。假设直方图中柱子的宽都为1。例如，输入数组[3，2，5，4，6，1，4，2]，其对应的直方图如图6.3所示，该直方图中最大矩形面积为12，如阴影部分所示。

分析：蛮力法

如果能逐一找出直方图中所有的矩形并比较它们的面积，就能得到最大矩形面积。

解：蛮力法

public class Test {
    public static void main(String[] args) {
        int[] heights = {3, 2, 5, 4, 6, 1, 4, 2};
        int result = largestRectangleArea(heights);
        System.out.println(result);
    }

    public static int largestRectangleArea(int[] heights) {
        int maxArea = 0;
        for (int i = 0; i < heights.length; i++) {
            int min = heights[i];
            for (int j = i; j < heights.length; j++) {
                min = Math.min(min, heights[j]);
                int area = min * (j - i + 1);
                maxArea = Math.max(maxArea, area);
            }
        }

        return maxArea;
    }
}

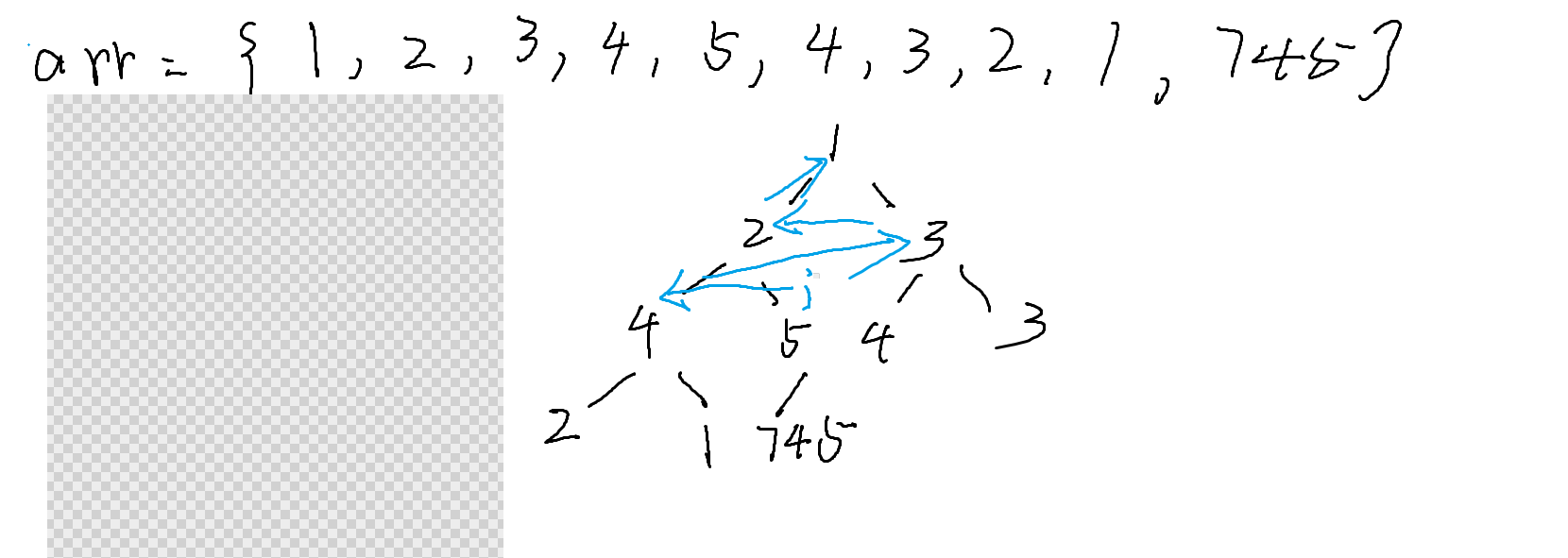
分析：分治法

这个直方图中最矮的柱子在数组中的下标是5，它的高度是1。这个直方图的最大矩形有3种可能。第1种是矩形通过这根最矮的柱子。通过最矮的柱子的最大矩形的高为1，宽是7。第2种是矩形的起始柱子和终止柱子都在最矮的柱子的左侧，也就是从下标为0的柱子到下标为4的柱子的直方图的最大矩形。第3种是矩形的起始柱子和终止柱子都在最矮的柱子的右侧，也就是从下标为6的柱子到下标为7的柱子的直方图的最大矩形。第2种和第3种从本质上来说和求整个直方图的最大矩形面积是同一个问题，可以调用递归函数解决。

解：分治法

public class Test {
    public static void main(String[] args) {
        int[] heights = {3, 2, 5, 4, 6, 1, 4, 2};
        int result = largestRectangleArea(heights);
        System.out.println(result);
    }

    public static int largestRectangleArea(int[] heights) {
        return helper(heights, 0, heights.length);
    }

    private static int helper(int[] heights, int start, int end) {
        if (start == end) {
            return 0;
        }

        if (start + 1 == end) {
            return heights[start];
        }

        int minIndex = start;
        for (int i = start + 1; i < end; i++) {
            if (heights[i] < heights[minIndex]) {
                minIndex = i;
            }
        }

        int area = (end - start) * heights[minIndex];
        int left = helper(heights, start, minIndex);
        int right = helper(heights, minIndex + 1, end);

        area = Math.max(area, left);
        return Math.max(area, right);
    }
}

分析： 单调栈法

由于已经计算了以每根柱子为顶的最大矩形面积，因此比较这些矩形面积就能得到直方图中的最大矩形面积

解：单调栈法

public class Test {
    public static void main(String[] args) {
        int[] heights = {3, 2, 5, 4, 6, 1, 4, 2};
        int result = largestRectangleArea(heights);
        System.out.println(result);
    }

    public static int largestRectangleArea(int[] heights) {
        Stack<Integer> stack = new Stack<>();
        stack.push(-1);

        int maxArea = 0;
        for (int i = 0; i < heights.length; i++) {
            while (stack.peek() != -1 && heights[stack.peek()] >= heights[i]) {
                int height = heights[stack.pop()];
                int width = i - stack.peek() - 1;
                maxArea = Math.max(maxArea, height * width);
            }

            stack.push(i);
        }

        while (stack.peek() != -1) {
            int height = heights[stack.pop()];
            int width = heights.length - stack.peek() - 1;
            maxArea = Math.max(maxArea, height * width);
        }

        return maxArea;
    }
}